GEOMETRÍA BACHILLERATO EJERCICIOS RECURSOS
GEOMETRÍA PARA BACHILLERATO. GEOMETRÍA ESPACIAL. RECURSOS Y EJERCICIOS RESUELTOS DE PUNTOS,
VECTORES, RECTAS Y PLANOS. DISTANCIAS:

ARTÍCULO CON NUMEROSO MATERIAL AUDIOVISUAL QUE RECORRE PRÁCTICAMENTE EL CONTENIDO
GEOMETRÍA 1º DE BACHILLERATO:
GEOMETRÍA PLANA, EN DOS DIMENSIONES:
-
- Recopilación de Fórmulas de Geometría para Matemáticas de 1º de Bachillerato
- Punto medio de un segmento
- Puntos y Rectas Notables en un Triángulo: Ortocentro, Circuncentro, Baricentro, Medianas, Mediatrices.
- Rectas Notables en un Triángulo: Alturas, Medianas, Mediatrices y Bisectrices
- Ejercicio Resuelto Cálculo del Circuncentro de un Triángulo
- Ejercicio Resuelto de Cálculo del Baricentro
- Ejercicio Resuelto Cálculo de la Mediatriz de un Segmento
- Ejercicio Resuelto Cálculo de la Mediatriz de un lado de un Triángulo
INTERESA IR AL SIGUIENTE ENLACE DE ESTA MISMA WEB, CON MATERIALES AUDIOVISUALES DE GEOMETRÍA PLANA. SE OBTIENEN ALTURAS, MEDIATRICES Y MEDIANAS, ASÍ COMO CIRCUNCENTRO, BARICENTRO Y ORTOCENTRO EN UN CASO CONCRETO: GEOMETRÍA PLANA PARA 1º DE BACHILLERATO
GEOMETRÍA 2º BACHILLERATO:
GEOMETRÍA EN TRES DIMENSIONES. GEOMETRÍA ESPACIAL
- Ecuaciones de la recta en 3 dimensiones, para Geometría de 2º de Bachillerato
- POSICIONES RELATIVAS DE DOS RECTAS
- Ecuaciones del plano, para Geometría de 2º de Bachillerato
- Fórmulas e indicaciones de Geometría y Métrica
- Condición de puntos alineados y coplanarios para matemáticas de 2º de Bachillerato
- Ejercicios Resueltos de Puntos Alineados para Matemáticas de Bachillerato
- Ejercicios Resueltos de Puntos Coplanarios para Matemáticas de Bachillerato
- Distancias entre Puntos, Rectas y Planos, para Matemáticas de 2º de Bachillerato
CIENCIA CON CONCIENCIA:
POSICIONES RELATIVAS DE DOS RECTAS EN EL PLANO:
Dos rectas en el plano se pueden cortar en un punto, ser paralelas o ser coincidentes.
En el espacio se añade una nueva relación: rectas que se cruzan.
Si imaginamos una recta como la línea que describe nuestra trayectoria, nuestra ruta a lo largo de la vida, ¿cómo te relacionas con los que te encuentras por el camino?.
¿Te has encontrado con otras «rectas coincidentes»?… o… ¿te has comportado como una recta paralela, manteniéndote siempre a una distancia prudencial de los que te has encontrado en el camino?. Ten en cuenta que para «coincidir» con otros hay que hacer un esfuerzo…
Y cuando tu recta se ha cortado con otra… ¿ha sido para bien?…
Y cuando tu recta se ha cruzado con otra… ¿aprovechaste el momento en que las dos estaban en el punto más cercano?
INTERIORIZO PROCESOS Y VALORES (PERFIL DE SALIDA DEL ALUMNADO)
EJERCICIO M2BE2001 JL, de conceptos básicos de geometría en el espacio (Puntos, vectores, módulo del vector=distancia entre dos puntos):
Considerando los puntos A (4,5,3) y B (2,1,4), obtener:
a.- El vector AB y el vector BA
b.- El módulo de cada uno de esos vectores, que coincidirá con la distancia que separa los dos puntos.
VÍDEO QUE RESUELVE EL EJERCICIO, DE FORMA ANALÍTICA Y A TRAVÉS DEL USO DE GEOGEBRA EN 3D PARA IPAD: https://youtu.be/DoETyRo4UXw
PREGUNTA HABITUAL DE LOS ALUMNOS:
Profe… ¿Puedo simplificar las coordenadas de un punto o vector?
La respuesta en el siguiente vídeo: https://youtu.be/eDwXwxrlyng
Pero ojo, el vídeo hace referencia al papel que juegan los puntos y los vectores en el tratamiento de las ecuaciones de las rectas, planos o cualquier otra historia de geometría relacionada. Si nos encontramos en Física y resulta que calculando por ejemplo el vector campo gravitatorio en algún sistema cartesiano de una distribución cualquiera de masas y te resulta el vector:
![]()
La has fastidiado, porque has dividido el valor del campo gravitatorio entre dos…, su módulo ha quedado dividido entre dos y eso no es correcto para esa distribución de masas concreta.
EJERCICIO M2BE2357:
Calcular la ecuación de la recta r, que pasa por los puntos A(1,2,3) y B(2,0,5).
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/YSICUg8INOw
EJERCICIO M2BE2358:
Determinar un punto y un vector de cada una de las siguientes rectas en el espacio:
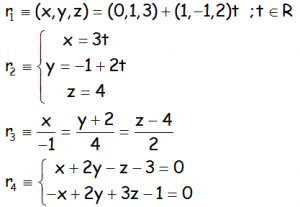
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/IP9ave1lBnk
EJERCICIO M2BE6:
Se dan dos rectas r y s mediante las siguientes ecuaciones:
![]()
Calcular la ecuación en forma implícita o general de un plano que pase por r y sea paralelo a s.
- INTERESA VER ECUACIÓN EN FORMA IMPLÍCITA DEL PLANO, EN LA ENTRADA ECUACIONES DEL PLANO
- INTERESA VER ECUACIÓN DE LA RECTA EN FORMA CONTÍNUA, EN LA ENTRADA ECUACIONES DE LA RECTA
VÍDEO QUE RESUELVE EN EL EJERCICIO EN FORMATO CLASE ONLINE: https://youtu.be/sO8SAK3UE24
EJERCICIO M2BE2021 JL: EJERCICIO DE PUNTO MEDIO Y PUNTO SIMÉTRICO
Sean los puntos A (4,8,-6) y B(8,-2,0)
a.- Hallar el punto medio del segmento AB.
b.- Hallar el punto simétrico de A respecto de B.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/0TVk1RY8XT0
Muy interesante la representación en geogebra 3D que se hace en el video de la situación
EJERCICIO M2BE7:
Dado el segmento AB, siendo sus puntos extremos A(1,0,0) y B(3,-4,4), hallar la ecuación del plano que es perpendicular a él y pasa por su punto medio.
INTERESA CONSULTAR ECUACIÓN NORMAL DEL PLANO, EN LA ENTRADA ECUACIONES DEL PLANO
PODRÍA NECESITARSE BUSCAR: PUNTO MEDIO DE UN SEGMENTO Y VECTOR QUE UNE DOS PUNTOS EN LA ENTRADA FÓRMULAS DE GEOMETRÍA
VÍDEO QUE RESUELVE EL EJERCICIO EN FORMATO CLASE ONLINE: https://youtu.be/FVLXi_37WMw
EJERCICIO M2BE1967:
Expresar la siguiente recta, indicada como intersección de dos planos, en forma paramétrica:
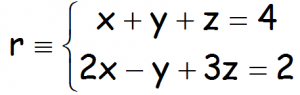
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/F95EVVYHnNE
EJERCICIO M2BE2360:
Dadas las rectas r y s:
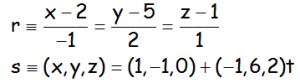
a.- Determinar la intersección de r y s.
b.- Calcular el plano que las contiene.
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/1JEiy3V9FDQ
EJERCICIO M2BE29:
Calcular k para que las siguientes rectas sean paralelas:
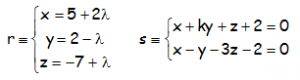
INTERESA CONSULTAR LA ECUACIÓN DE LA RECTA EN FORMA IMPLÍCITA EN LA ENTRADA ECUACIONES DE LA RECTA
INTERESA VER CONDICIÓN QUE CUMPLEN LAS RECTAS PARALELAS EN FÓRMULAS DE GEOMETRÍA
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/e0pXwMJ9QTg
EJERCICIO DE ESTUDIO DE POSICIONES RELATIVAS DE DOS RECTAS MEDIANTE RANGOS:

EJERCICIO M2BE2361:
Estudiar la posición relativa de las dos rectas siguientes, s y r:
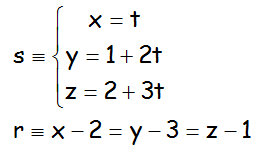
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/5M_Pg7-YbwA
EJERCICIO M2BE1958:
Estudiar la posición relativa de las rectas:
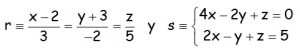
INTERESA IR A ESTUDIO DE LA POSICIÓN RELATIVA DE DOS RECTAS
VÍDEO, EN FORMATO CLASE, QUE RESUELVE EL EJERCICIO, CON EXPLICACIÓN TEÓRICA DEL PROCESO: https://youtu.be/APqCSw2KY40
EJERCICIO M2BE2359:
a.- ¿Están alineados los puntos A(3,-2,1), B(5,-6,9) y C(4,4,5)?.
b.- Calcular el plano perpendicular a la recta AB que pasa por C.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/HaZzkoXgjmg
POSICIONES RELATIVAS DE RECTAS Y PLANOS EN EL ESPACIO:
EJERCICIOS M2BE2362:
a.- Estudiar la posición relativa del plano y la recta siguientes:
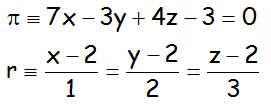
b.- Estudiar la posición relativa del plano y la recta siguientes:
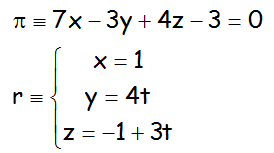
c.- Estudiar la posición relativa del plano y la recta siguientes:
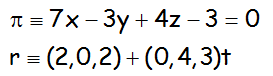
VÍDEO CON LA SOLUCIÓN DE ESTOS TRES EJEMPLOS, QUE CONTIENE ASPECTOS TEÓRICOS DE INTERÉS: https://youtu.be/OUaY0DlgV4k
POSICIÓN RELATIVA DE TRES PLANOS:
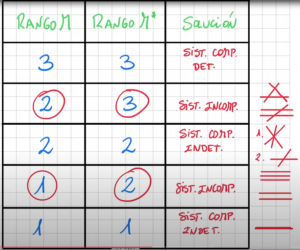
EJERCICIO M2BE2363:
Estudiar la posición relativa de los tres planos siguientes:
π1 ≡ x + 2y + 3z – 3 = 0
π2 ≡ – 2x + 3y + 7z + 9 = 0
π3 ≡ – 2x – 4y – 6z + 6 = 0
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO Y ASPECTOS TEÓRICOS DE INTERÉS PARA SU RESOLUCIÓN: https://youtu.be/DGtMz46hzBY
EJERCICIO M2BE1989JL (EBAU CANARIAS 2021):
Dados los siguientes puntos en el espacio tridimensional: A(0,-2,3), B(1,-1,4), C(2,3,3) y D(4,5,5)
a.- Comprobar que los cuatro puntos son coplanarios. A continuación, calcular la ecuación del plano que los contiene.
b.- Calcular la ecuación de la recta r, perpendicular al plano π, que pasa por el punto A.
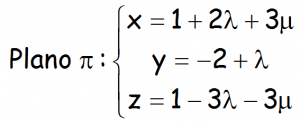
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/SYfqOEhBSw4
EJERCICIO M2BE2364:
Sea A(1, 3, 5) y B(-3, 1, 3) dos puntos en el espacio que determinan la recta r y π el plano:
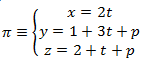
a) Calcular el plano π’ paralelo al plano π que pasa por el punto medio de A y B. (Indicar π’ en forma general)
b) Calcular el plano π´´ que es perpendicular a la recta r, y pasa por el punto de intersección del plano π y la recta r.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/yYsPwRUPmN8
EJERCICIO M2BE1990JL (EBAU CANARIAS 2021):
Dado el plano π: -x+3y+2z+5=0
Y las rectas secantes:
![]()
a.- Sea A el punto de intersección de las rectas r y s.
Hallar la ecuación de la recta que es perpendicular al plano π y que pasa por A.
b.- Calcular el ángulo que forman las rectas r y s.
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO
EJERCICIO M2BE1991JL (EBAU CANARIAS 2021):
Dadas las siguientes ecuaciones en el espacio tridimensional:
r: 5-x=y-3=5-z
π: 3x-4y-8z+35=0
a.- Comprobar que la recta r y el plano π se cortan en un punto.
b.- Calcular la ecuación del plano que pasa por el punto A (2,2,2), paralelo a la recta r y perpendicular al plano π.
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO
EJERCICIO M2BE1999 JL:
Sean los puntos A(1, 2, 3) y B(3, -4, 1) y la recta r siguiente:
![]()
a) Calcular la recta que pasa por el punto medio de A y B y el punto de intersección de r y el plano π: 2x-y+z+3=0
b) Calcula el plano que contiene a los puntos A y B, y es paralelo a la recta r.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/H_h-4mb3zwA
EJERCICIO M2BE31 (EBAU CANARIAS JUNIO 2022):
En el espacio tridimensional conocemos las ecuaciones siguientes:
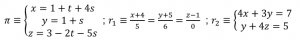
a) Calcula la ecuación de la recta 𝑠, perpendicular al plano 𝜋 𝑦 que contiene el punto de intersección de las rectas 𝑟1 y 𝑟2.
b) ¿Es cierto que el ángulo entre las rectas 𝑟1 y 𝑟2 es menor de 45º? Justifícalo
IR AL VÍDEO CON LA RESOLUCIÓN EJERCICIO: https://youtu.be/fvvQ4YyPKkQ
EJERCICIO M2BE2032 (EBAU CANARIAS JUNIO 2022):
En el espacio tridimensional conocemos las ecuaciones de las rectas siguientes:
![]()
a) Estudia la posición relativa de las rectas 𝑟 y 𝑠
b) Calcula la ecuación del plano 𝜋 paralelo a la recta 𝑠 que contiene a la recta 𝑟.
Halla el punto de corte de dicho plano 𝜋 con la recta:
![]()
IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/td-Gnm3qNe0
EJERCICIO M2BE2159:
Sean los puntos A (3, 1, 5), B (-2, -1, 4) y C (8, 3, 6).
a) Demostrar si los tres puntos están alineados o no.
b) Calcular la recta s perpendicular a la recta determinada por A y B, sabiendo que s pasa por P(-2, 3, -1).
IR AL ARTÍCULO DONDE SE ENCUENTRA LA SOLUCIÓN DEL EJERCICIO: EXAMEN GEOMETRÍA, ÁLGEBRA, ANÁLISIS PARA MATEMÁTICAS 2º BACHILLERATO
EJERCICIO M2BE2167:
Sean los puntos A(3, 1, 5), B(-2, -1, 4) y C(2, 3, 2).
Calcular la ecuación en forma general del plano π que contiene a los tres puntos.
IR AL ARTÍCULO DONDE SE ENCUENTRA LA SOLUCIÓN DEL EJERCICIO: EXAMEN BLOQUES ANÁLISIS, ÁLGEBRA Y GEOMETRÍA. MATEMÁTICAS II. 2º BACHILLERATO
EJERCICIO M2BE2168:
Sean los puntos B(-2, -1, 4) y C(2, 3, 2). Calcular la posición relativa de la recta m que pasa por B y C, y la recta n:
![]()
IR AL ARTÍCULO DONDE SE ENCUENTRA LA SOLUCIÓN DEL EJERCICIO: EXAMEN BLOQUES ANÁLISIS, ÁLGEBRA Y GEOMETRÍA. MATEMÁTICAS II. 2º BACHILLERATO
EJERCICIO M2BE2188:
Sea r la recta que pasa por los puntos A(1, 0, 1) y B(2, 1, 2) y s la recta s ≡ x – 2 = 2 – y = z
a) Indica la posición relativa de r y s.
b) Calcula un plano (forma general) paralelo a r y que contenga a s.
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA DE EXAMEN DE MATEMÁTICAS II, 2º DE BACHILLERATO. ANÁLISIS, ÁLGEBRA DE MATRICES, GEOMETRÍA Y PROBABILIDAD
EJERCICIO M2BE2244: EBAU CANARIAS JUNIO 2014
Dados los puntos A (-1,0,3), B (2,4,1) y C (-4,3,1):
a.- Estudiar si los puntos A,B y C están alineados.
b.- Hallar la ecuación de la recta paralela al segmento AB y que pasa por C. Expresarla como intersección de dos planos.
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIOS PARA CONFIRMAR QUE SE HA APRENDIDO EL CONTENIDO MOSTRADO:
EJERCICIO M2BE390:
Calcular la ecuación del plano que contiene a la recta r y es paralelo a la recta s, siendo r y s las rectas siguientes:
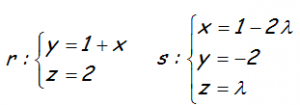
SOLUCIÓN: -x+y-2z+3=0
EJERCICIO M2BE1186:
Calcula la ecuación de una recta que pasa por el punto de intersección del plano π, con la recta r, y es paralela a la recta s, siendo π, r y s los siguientes:
![]()
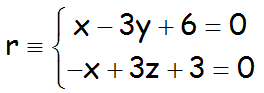
![]()
SOLUCIÓN:
![]()
.
EJERCICIO M2BE1691:
Estudiar la posición relativa de las siguientes rectas:
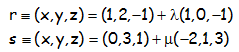
SOLUCIÓN: Se cortan en (2,2,-2)
EJERCICIO M2BE1188:
Se considera la recta r y el plano π:
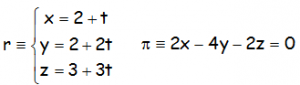
A.- Determinar la ecuación del plano π1 que pasa por el punto P(1,1,1) y es paralelo al plano π.
B.- Determinar la ecuación general del plano π2 que contiene a la recta r y pasa por el punto P
SOLUCIONES: x-2y-z+2=0; -x-y+z+1=0
EJERCICIO M2BE2000 JL, DE ÁNGULOS EN EL ESPACIO:
a.- Hallar el ángulo existente entre estas dos rectas:
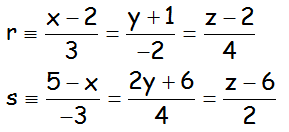
b.- Hallar el ángulo que forman los siguientes dos planos:
π1 ≡ 3x – 2y + z – 2 = 0
π2 ≡ x – y + 3 = 0
c.- Hallar el ángulo que forman la recta r y el plano π:
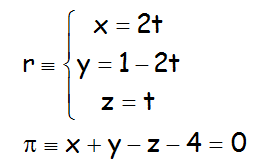
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/Dcy_X9dpr8M
EJERCICIO M2BE2209:
Considere el plano π: x+y+z=1 y la recta r que pasa por los puntos P (0, 0, 6) y Q (1, 2, 3).
a.- Estudie la posición relativa de la recta r y el plano π.
b.- Calcular la recta s, perpendicular al plano , que pasa por el punto simétrico de P respecto de Q.
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO QUE ESTÁ INCLUÍDO EN UNA PRUEBA DE EXAMEN GLOBAL PARA MATEMÁTICAS II DE 2º DE BACHILLERATO: EXAMEN GLOBAL MATEMÁTICAS II 2º BACHILLERATO. GEOMETRÍA, ÁLGEBRA DE MATRICES, PROBABILIDAD, ANÁLISIS (OPTIMIZACIÓN)
EJERCICIO M2BE2217:
Considere el plano π:
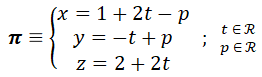
y la recta r que pasa por los puntos P(1, 0, 6) y Q(1, 2, -3).
a) Estudiar la posición relativa del plano y la recta r.
b) Calcular la recta s, que es perpendicular a la recta r y pasa por el punto J(0, -5, -14).
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN FINAL GLOBAL MATEMÁTICAS 2º BACHILLERATO
EJERCICIO M2BE2267: EBAU CANARIAS 2020
Consideremos la recta r siguiente:
![]()
y el plano π1 ≡ x – y + 3z = 12
a.- Calcular la ecuación del plano π2 que contiene a la recta r y es perpendicular al plano π1.
b.- Sabiendo que la recta r corta al plano π1, averigüe el punto de intersección,
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2377:
Teniendo en cuenta la recta r y el plano π siguientes,
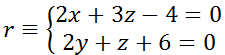
![]()
a.- Calcular una recta que pase por el punto de intersección de r y π , y sea paralela a la recta
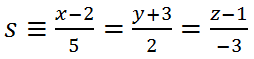
b.- Calcular la posición relativa de las rectas r y s.
c.- Calcular un plano β que contiene a r y pasa por el punto P(-1, 1, 2).
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO Y SUS APARTADOS: EXAMEN ANÁLISIS, ÁLGEBRA Y GEOMETRÍA PARA MATEMÁTICAS DE 2º DE BACHILLERATO
EJERCICIO M2BE2382, EBAU CANARIAS:
Hallar la ecuación de la recta que verifica simultáneamente las siguientes condiciones:
- es paralela a los planos de ecuaciones: π1 ≡ x – 3y + z = 0 y π2 ≡ 2x – y + 3z = 5
- pasa por el punto P(2, -1, 5)
EJERCICIO M2BE2383, EBAU CANARIAS:
Dados los planos π1 ≡ x – y + 3 = 0 y π2 ≡ 2x + y – z = 0, calcular:
a.- La ecuación de la recta s paralela a los planos π1 y π2 que pasa por el punto B(2, 2, 3)
b.- El ángulo que forman los planos π1 y π2 .
EJERCICIO M2BE2384, EBAU CANARIAS:
Dadas las rectas siguientes r y s:
![]()
a.- Estudiar la posición relativa de r y s.
b.- Hallar la ecuación del plano perpendicular a la recta r, y que contiene el punto A(11, -2, 5)
EJERCICIO M2BE2385, EBAU CANARIAS 2021:
Dados los siguientes puntos en el espacio tridimensional:
A(0, -2, 3), B(1, -1, 4), C(2, 3, 3) y D(4, 5, 5)
a.- Comprobar que los cuatro puntos son coplanarios. A continuación, calcular la ecuación del plano que los contiene.
b.- Calcular la ecuación de la recta r, perpendicular al plano π, que pasa por el punto A, siendo π el plano siguiente :
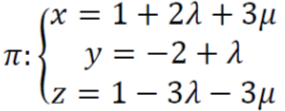
EJERCICIO M2BE2386:
Hallar el plano perpendicular a la recta AB que contiene al simétrico de A respecto de B siendo A(1,2,3) y B(-1,0.3).
SOLUCIÓN: -2x+y-3z-19=0
EJERCICIO M2BE2387:
Estudiar la posición relativa de la recta dada como intersección de los planos: x+2y-5=0; 3x+y-9=0 con el plano -2x+y-3z-19=0
En caso de cortarse, hallar el punto de corte.
SOLUCIÓN: (-3, 4, -3)
EJERCICIO M2BE2147:
Hallar la ecuación de la recta r perpendicular a la recta s, que pase por el punto P(1,-1,3), siendo s:
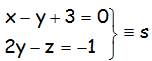
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO; CUESTIONES CON CIERTA COMPLICACIÓN DE GEOMETRÍA EN EL ESPACIO. RECTAS Y PLANOS
EJERCICIO M2BE2149:
Siendo la recta r que se muestra y el punto A (0,-1,-2). Calcular la recta s perpendicular a r que pasa por A, expresándola en forma contínua.
![]()
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO; CUESTIONES CON CIERTA COMPLICACIÓN DE GEOMETRÍA EN EL ESPACIO. RECTAS Y PLANOS
EJERCICIO M2BE2150:
Se consideran los puntos A(2,-1,1) y B(-2,3,1) que determinan la recta r.
a.- Calcular la recta perpendicular a r que pasa por el punto P(-4,17,0)
b.- Calcular la ecuación del plano respecto del cual los puntos A y B son simétricos.
SOLUCIÓN: (x,y,z)=(-4,17,0)+(-6,-6,1)·t; -4x+4y-4=0
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO; CUESTIONES CON CIERTA COMPLICACIÓN DE GEOMETRÍA EN EL ESPACIO. RECTAS Y PLANOS
EJERCICIO M2BE2424:
Teniendo en cuenta la recta r y el punto P(5, -6, -3), calcula la recta s que es perpendicular a r y pasa por el punto P, siendo r la recta siguiente:
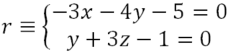
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN TERCER TRIMESTRE MATEMÁTICAS II DE 2º DE BACHILLERATO: ANÁLISIS, ÁLGEBRA, GEOMETRÍA, PROBABILIDAD

Comments are closed, but trackbacks and pingbacks are open.