FRACCIÓN GENERATRIZ DECIMAL RACIONAL
OBTENCIÓN DE LA FRACCIÓN GENERATRIZ DE UN NÚMERO RACIONAL: PASO DE NÚMERO DECIMAL A FRACCIÓN:

Para pasar un número decimal a fracción, hay que distinguir dos casos:
Si el número es decimal exacto:
Es muy sencillo, ya que basta con dividirlo (como si no tuviera la coma) entre la potencia de 10 que tenga como exponente el número de cifras de la parte decimal (a la izquierda de la coma).
EJEMPLO: Pasar a fracción los siguientes números decimales exactos.
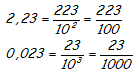
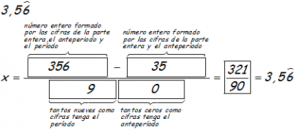
Si el número es periódico:
La cuestión se complica pudiéndose utilizar la siguiente fórmula:
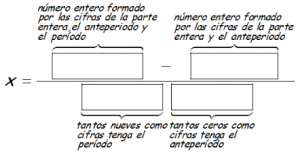
Donde:
La parte entera son los números delante (a la izquierda) de la coma.
El anteperíodo son los números después (a la derecha) de la coma, que no forman parte del período; es decir los números entre la coma y el periodo. Podría ser que no haya anteperíodo porque todo lo de después de la coma sea periodo.
El período es sólo la parte periódica.
En el numerador de la fórmula, se realiza la resta de dos números enteros, los indicados según el esquema:
«número entero formado por las cifras de la parte entera, el anteperíodo y el período» menos «número entero formado por las cifras de la parte entera y el anteperiodo»
En el denominador SÓLO UN NÚMERO que es:
poner «tantos nueves como cifras tenga el período» y a continuación (en el mismo número) «tantos ceros como cifras tenga el anteperíodo» (podría ser que el anteperíodo no exista y no se pondría nada)
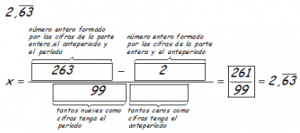
EJEMPLOS: Pasar a fracción los siguientes números decimales periódicos.