EJERCICIOS DE ANÁLISIS DE FUNCIONES

EJERCICIOS ANÁLISIS FUNCIONES BACHILLERATO

EJERCICIOS DE ANÁLISIS DE FUNCIONES PARA BACHILLERATO:

---

ASPECTOS FORMALES LOMLOE AL FINAL DEL ARTÍCULO

---

EJERCICIO M2BE2031:

Realizar el estudio completo de la siguiente función:

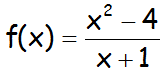
CONTRASTAR LO OBTENIDO ANALÍTICAMENTE CON LA REPRESENTACIÓN GRÁFICA EN GEOGEBRA

EJERCICIO M2BE2032:

Realizar el estudio completo de la siguiente función:

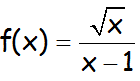
CONTRASTAR LO OBTENIDO ANALÍTICAMENTE CON LA REPRESENTACIÓN GRÁFICA EN GEOGEBRA

SOBRE LA EJECUCIÓN DE ESTE EJERCICIO EN CLASE: Manualmente es terrible la 2ª derivada, pero corresponde a la expresión que se muestra, utilizando la aplicación wiris; que además en la búsqueda del punto de inflexión y al resolver la ecuación correspondiente nos devuelve dos soluciones de las que sólo sirve una, la primera, por estar la otra fuera del dominio. Esta solución válida numéricamente es x=0,1547, que se observa en la representación que efectivamente tiene un punto de inflexión:

EJERCICIO M2BE2002 JL:

Realizar el estudio de las asíntotas horizontales de la siguiente función:

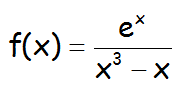
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/mfTP_-Sgen0

EJERCICIO M1BE2018:

Representar la función f(x), haciendo un estudio completo de la misma:

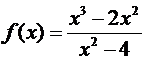
EJERCICIO M2BE2017:

Dada la función:

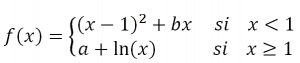
a.- Estudia los valores de los parámetros a y b para que la función f(x) sea continua y derivable en ℜ. Escribe la función resultante f(x).

b.- Tomando los valores a=-2 y b=1, calcula la ecuación de la recta tangente en x=e.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/foUIAm2GnC4

EJERCICIO M2BE2124:

Sea la función f(x) = 1 + 1/x ,

a.- Determinar el dominio y los intervalos de crecimiento y de decrecimiento de la función f(x) (monotonía de la función).

b.- Dada la función g(x) = (5-x)/2 , hallar el área de la región acotada por las gráficas de las funciones f(x) y g(x).

EJERCICIO M2BE2125:

Sea la función f(x) = x³ + cos(πx) . Se pide:

a.- Calcular la recta tangente a la gráfica de f(x) en x=1.

b.- Calcular:

EJERCICIO M2BE2277:

Dada la siguiente función f(x):

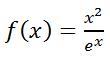
a.- Determinar los intervalos de crecimiento y los de decrecimiento.

b.- Calcular los máximos y mínimos relativos.

IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24

MÁS EJERCICIOS DE ANÁLISIS DE FUNCIONES PARA BACHILLERATO EN:

https://achimagec.com/category/asignaturas-fisica-quimica-matematicas/matematicas/matematicas-2o-bac/analisis-de-funciones/

EJERCICIO M1BE2019:

PLANTEARSE LAS SIGUIENTES PREGUNTAS TIPO TEST:

TEST DOMINIO ASINTOTA

IR A LAS SOLUCIONES DE LAS PREGUNTAS: SOLUCIONES VARIAS ALUMNOS

 

PUEDE INTERESAR CONSULTAR LA SIGUIENTE PRUEBA/EXAMEN RESUELTA DE ESTE CONTENIDO PARA MATEMÁTICAS DE 2º DE BACHILLERATO:

PRUEBA DE ANÁLISIS PARA MATEMÁTICAS DE 2º BACHILLERATO

---

ASPECTOS FORMALES:

SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS:

• COMPETENCIA MATEMÁTICA Y EN CIENCIA, TECNOLOGÍA E INGENIERÍA (STEM), concretamente el DESCRIPTOR OPERATIVO STEM1.
• COMPETENCIA EN COMUNICACIÓN LINGÜÍSTICA (CLL), concretamente el DESCRIPTOR OPERATIVO CCL2.
• COMPETENCIA DIGITAL (CD), concretamente el DESCRIPTOR OPERATIVO CD1.

• COMPETENCIA PERSONAL, SOCIAL Y DE APRENDER A APRENDER (CPSAA), concretamente el DESCRIPTOR OPERATIVO CPSAA1.1
• COMPETENCIA EMPRENDEDORA (CE), concretamente el DESCRIPTOR OPERATIVO CE1

CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS I DE 1º DE BACHILLERATO

MATI1BAC1.1 , MATI1BAC1.2 , MATI1BAC2.1 , MATI1BAC2.2 , MATI1BAC3.1 , MATI1BAC4.1 , MATI1BAC5.1 , MATI1BAC5.2 , MATI1BAC6.1 , MATI1BAC6.2 , MATI1BAC7.1 , MATI1BAC7.2 , MATI1BAC8.1 , MATI1BAC8.2 , MATI1BAC9.1 , MATI1BAC9.2 , MATI1BAC9.3 

SE OBSERVAN LAS COMPETENCIAS ESPECÍFICAS DE MATEMÁTICAS I Y II Y ESTÁN HIPERVINCULADOS A LOS DESCRIPTORES OPERATIVOS DE LAS COMPETENCIAS CLAVE