EXAMEN RESUELTO ANÁLISIS FUNCIONES
MATEMÁTICAS I 1º BACHILLERATO CIENCIAS
EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES. SEGUNDA PRUEBA DEL TERCER TRIMESTRE DEL CURSO 23 24, PARA MATEMÁTICAS I DE 1º BACHILLERATO (X676), REALIZADO EN «EL PILAR»:

PRUEBA EVALUADORA QUE INCLUYE SABERES BÁSICOS DE MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS RELATIVOS A:
- SIGUE EL PROCESO DETERMINADO SEGÚN: MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- SE HA UTILIZADO, EN LA SEGUNDA PARTE DEL ÚLTIMO EJERCICIO DE LA PRUEBA, LA DINÁMICA INDICADA EN: LA MOTIVACIÓN DE LOS PUNTOS EXTRA
- PUEDE INTERESAR LA CONSULTA DE LAS SIGUIENTES CLASES DE REFUERZO, PREVIAS A LA REALIZACIÓN DE LA PRUEBA:
- CLASE ON-LINE DE INICIO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO
- CLASE DE REFUERZO DE CÁLCULO DE LÍMITES PARA MATEMÁTICAS DE 1º DE BACHILLERATO EN «EL PILAR»
- CLASE ON LINE DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO. PROGRAMA DE REFUERZO DE CONTENIDOS SIGNIFICATIVOS, DEL 25 DE ABRIL DE 2024
LOS ENUNCIADOS DE ESTA PRUEBA DE ANÁLISIS DE FUNCIONES (X676) PARA 1º DE BACHILLERATO:
X676 EXAMEN MATEMÁTICAS I 1º BACHILLERATO ANÁLISIS PRU 2 2324_v1LOS EJERCICIOS DE LA PRUEBA Y SUS SOLUCIONES PASO A PASO:
EJERCICIO M1BE2487:
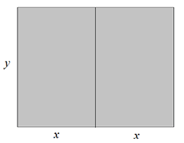
Un granjero llamado Omar dispone de 200 metros de valla para delimitar dos corrales adyacentes rectangulares de igual tamaño según se muestra en la figura. ¿Qué dimensiones debe elegir para que el área encerrada en los corrales sea máxima?
LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE OPTIMIZACIÓN:
EJERCICIO MIBE2487 PROBLEMA OPTIMIZACIÓN CORRALES ADYACENTES_v1
EJERCICIO M1BE2488:
Para la siguiente función f(x), calcular:
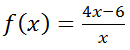
a) Dominio e imagen (recorrido).
b) Asíntotas.
c) Monotonía y extremos.
d) Curvatura y puntos de inflexión.
e) Representación.
LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO:
EJERCICIO MIBE2488 ANÁLISIS FUNCIÓN RACIONAL_v1
EJERCICIO M1BE2489:
a.- Dibujar las gráficas f(x) = x2 + 4x + 5 y g(x) = 5 , y sombrear el área que encierran.
b.- Hallar el área que encierran las funciones anteriores.
LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO:
EJERCICIO MIBE2489 REPRESENTACIÓN ÁREA FUNCIONES_v1
EJERCICIO M1BE2490:
Dada la función f(x) = ax3 + bx + c , determinar los valores a, b y c, si sabemos que tiene un extremo en M(2, – 6), y además, la recta tangente en el punto de abscisa x = 1 es paralela a la recta y + 9x =2.
LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO:
