PRUEBA EXAMEN RESUELTA ANÁLISIS
MATEMÁTICAS I 1º BACHILLERATO CIENCIAS
EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES. TERCERA PRUEBA DEL TERCER TRIMESTRE DEL CURSO 23 24, PARA MATEMÁTICAS I DE 1º BACHILLERATO (X677), REALIZADO EN «EL PILAR»:
PRUEBA EVALUADORA QUE INCLUYE SABERES BÁSICOS DE MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS RELATIVOS A:
- SIGUE EL PROCESO DETERMINADO SEGÚN: MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- PUEDE INTERESAR LA CONSULTA DE LAS SIGUIENTES CLASES DE REFUERZO, PREVIAS A LA REALIZACIÓN DE LA PRUEBA:
- CLASE ON-LINE DE INICIO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO
- CLASE DE REFUERZO DE CÁLCULO DE LÍMITES PARA MATEMÁTICAS DE 1º DE BACHILLERATO EN «EL PILAR»
- CLASE ON LINE DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO. PROGRAMA DE REFUERZO DE CONTENIDOS SIGNIFICATIVOS, DEL 25 DE ABRIL DE 2024
LOS ENUNCIADOS DE ESTA PRUEBA DE ANÁLISIS DE FUNCIONES (X677) PARA 1º DE BACHILLERATO:
LOS EJERCICIOS DE LA PRUEBA Y SUS SOLUCIONES PASO A PASO:
EJERCICIO M1BE2491:
Hallar los valores de los parámetros a y b para que la función f(x) definida a continuación, sea continua y derivable en el conjunto de los números reales:
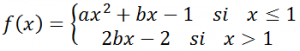
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE2492:
Para la siguiente función f(x), definida a continuación:
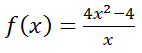
a) Dominio y cortes con los ejes
b) Asíntotas
c) Monotonía y extremos
d) Representación
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE2493:
Hallar el límite de la siguiente función:
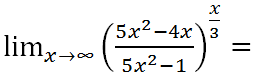
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE2494:
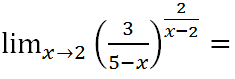
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M1BE2495:
Calcula los coeficientes a, b y c de la función f(x) = x4 + ax3 + bx2 + cx , sabiendo que:
a) La ecuación de la recta tangente a f(x) en x=0 es y=x.
b) Tiene un extremo relativo en el punto (–1, 0).
LA SOLUCIÓN PASO A PASO DEL EJERCICIO: