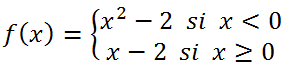ANÁLISIS FUNCIONES MATEMÁTICAS BACHILLERATO
CLASE ON LINE VÍDEO
CLASE ON LINE DE INICIO DE ANÁLISIS DE FUNCIONES PARA 1º DE BACHILLERATO:
Clase on-line de análisis de funciones, para Matemáticas de 1º de Bachillerato de la Modalidad de Ciencias y Tecnología realizada en el Instituto «El Pilar», uno de los tres Institutos Diocesanos de Canarias.
VÍDEO CON LA CLASE ON LINE DE ANÁLISIS DE FUNCIONES:
FUNCIONES ELEMENTALES: https://youtu.be/jsA89Ktt5zI?si=mLrFXbgJlu7xQits
La dinámica se realiza dentro del PROGRAMA DE MEJORA DEL APRENDIZAJE del Centro. Los alumnos que lo desean, fuera del horario lectivo, por la tarde, asisten a ella a través de Teams, en el equipo configurado al efecto. Se aporta aquí con la idea de que lo aprovechen incluso los que no han podido estar en tiempo real.
En la clase de hora y media de duración, de cuyo vídeo aportamos el enlace, se resuelven y se explican las siguientes cuestiones de ANÁLISIS DE FUNCIONES para este nivel de MATEMÁTICAS de 1º de BACHILLERATO.
El desarrollo de la clase, a modo de sinopsis del vídeo, ha sido el siguiente:
FUNCIONES LINEALES:
Se representan funciones lineales, utilizando la clásica tabla de valores e incluso los conceptos de la ordenada en el origen y de la pendiente para la obtención de la recta que corresponde en cada caso. Se introduce el modo de obtener los puntos de corte con los ejes. Esta primera parte se trabaja a través de las funciones:
f(x) = 4; f(x) = 3, funciones horizontales o constantes
f(x) = 2x; función lineal
f(x) = 2x + 1; f(x) = 2x + 3 , funciones afín
f(x) = – x + 1, con pendiente negativa.
FUNCIONES CUADRÁTICAS:
Se representan funciones cuadráticas, a través de los puntos de corte con los ejes, así como obteniendo el vértice de la parábola. Se indica que el signo del coeficiente del monomio de 2º grado según sea positivo o negativo, nos da información de si la parábola es cóncava «∪» o convexa «∩».
Se trabaja con las funciones cuadráticas siguientes, que se representan según nos indica lo descrito anteriormente:
f(x) = x2 – 3x;
f(x) = – x2 – 2x + 8; que además se contrastan con la aplicación geogebra , obteniendo incluso con las herramientas que suministra de vértice y puntos de corte.
Se aprovecha la aplicación geogebra para contrastar las funciones lineales que se trabajaron inicialmente.
FUNCIONES A TROZOS:
Se representa con detalle la siguiente función a trozos, se contrasta con geogebra y se comenta la continuidad. Se indica además, a través de la representación, la imagen o el recorrido de la función, así como el dominio.
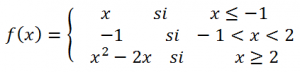
FUNCIONES RACIONALES:
Se trabaja con la siguiente función racional, estudiando el dominio en un primer momento.
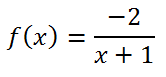
Se confirma la presencia de asíntota vertical introduciendo el concepto de límite a la izquierda y a la derecha de ese lugar posible de asíntota vertical, analizando la tendencia de la función a cada lado de la asíntota.
Del mismo modo e introduciendo el concepto de límite en el infinito se confirma la presencia de asíntota horizontal en el infinito. Del mismo modo con el menos infinito.
Todas estas cuestiones se contrastan con la representación a través de geogebra.
PARA FINALIZAR Y A MODO DE REPASO A SOLICITUD DE LOS ALUMNOS, se estudia y representa esta nueva función a trozos, igualmente con su contraste con geogebra: