RELATIVIDAD FÍSICA BACHILLERATO LORENTZ
RELATIVIDAD PARA FÍSICA DE 2º DE BACHILLERATO:

Hemos preparado este material audiovisual, que se complementa con el documento, bastante más extenso, que se añade al final de este artículo, donde se abordan los conceptos teóricos sobre la Teoría de la Relatividad, que se aplican en este nivel, así como se proponen otros ejercicios, aparte de los que se resuelven en los videos que se suministran.
Las ecuaciones que nos permiten abordar este contenido, son las Transformaciones de Lorentz:
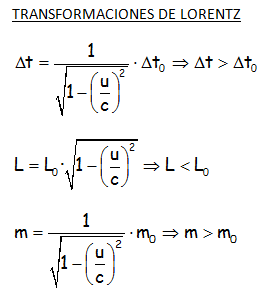
PUEDE RESULTAR INTERESANTE IR AL ARTÍCULO DE OBTENCIÓN DE LA TRANSFORMACIÓN DE LORENTZ PARA LOS INTERVALOS DE TIEMPO MEDIDO POR LOS DOS OBSERVADORES: OBTENCIÓN DE LA TRANSFORMACIÓN DE LORENTZ PARA INTERVALOS DE TIEMPO. RELATIVIDAD
INCLUSO, LA CONSULTA DEL ARTÍCULO: UNA CONFIRMACIÓN DE LA TEORÍA DE LA RELATIVIDAD. LA VISITA DE LOS MUONES A LA SUPERFICIE DE LA TIERRA , COMO EVIDENCIA DE LA VERACIDAD DE LA RELATIVIDAD EN LO QUE RESPECTA A LA CONTRACCIÓN DE LAS LONGITUDES.
Utilización de las transformaciones de Lorentz, para relacionar los intervalos de tiempo, diferentes, medidos por un observador en reposo y por otro que se mueve a velocidades próximas a la de la luz.
EJERCICIO 1, QUE SE RESUELVE EN EL VÍDEO, conjuntamente con pinceladas teóricas:
Vega es una estrella de la constelación de la Lira. Es la quinta estrella más brillante del cielo nocturno y está relativamente cerca, a sólo 25 años luz de la Tierra.
Una nave espacial parte hacia ella, con una velocidad de 0,82c (2,46·108 m/s). Calcular el tiempo en años que invierte la nave en alcanzar dicha estrella, según los relojes terrestres y según los relojes de a bordo. DATO: c=3·108 m/s.
Utilización de las relaciones de Lorentz, para calcular la velocidad de una nave, en la que sorprende la diferencia entre las longitudes medidas por un observador en reposo y otro en movimiento. El enunciado intenta motivar, o al menos desarrollar simpatías, contextualizándolo en Star Trek.
EJERCICIO 2, QUE SE RESUELVE EN EL VÍDEO:
Un centinela del Imperio Klingon, desde su planeta Qo’nos, en el Cuadrante Beta, mientras realiza su guardia, informa a su comandante que el nuevo modelo de nave Enterprise, cuando pasa por delante de él mide 790.8 metros de largo.
El Klingon fue arrestado, por inepto, ya que su comandante sabía que esa nave, fabricada en la Tierra mide exactamente 823.5 metros.
Suponiendo que el movimiento de la nave respecto del centinela era de traslación uniforme en la dirección y sentido del movimiento del centinela, y teniendo en cuenta que te has convertido en asesor científico del abogado defensor del pobre Klingon, argumenta con detalle los motivos por los que el acusado de inepto es absolutamente inocente.
Dato: c=3·108 m/s
Se aborda en el marco de la Teoría de la Relatividad, el problema de la variación en la medida de las masas, dependiendo del observador.
EJERCICIO F2BE2764, Que se resuelve en el vídeo:
Una partícula cargada de 2 mg de masa en reposo, por efecto de aplicarle una diferencia de potencial considerable, adquiere una velocidad de 1,3·108 m/s. Hallar la masa de la partícula cuando se está moviendo a esa velocidad. DATO: c = 3·108 m/s
EJERCICIO F2BE2219:
En el encuentro anual de carreras de escobas de los Colegios de Magia y Hechicería, Draco Malfoy es el participante seleccionado de Hogwarts, con su Nimbus 2020 último modelo, para esta prueba cronometrada.
Dumbledore desde la tribuna, en el viaje de ida y vuelta de Draco mide 5 minutos y medio, a lo que Draco presenta una reclamación, puesto que él en su escoba y con su reloj, ha medido exactamente 4 minutos. DATO: c=3·108 m/s
a.- Podrías tranquilizar a Draco, explicando con todo lujo de detalles, que tanto él como Dumbledore tienen razón.
b.- Hallar la velocidad a la que se mueve Draco.
c.- El esmirriado de Drago, tuvo que pesarse antes de la prueba, para saber la categoría en la que participaba y resultó tener en ese momento, una masa de 67 kg. Hallar su masa relativista la masa que se observa mientras está completando el recorrido.
d.- Si el modelo Nimbus 2020, tiene una longitud de 2,03 m, incluido el penacho de la escoba, hallar la longitud que parece tener, para Dumbledore, mientras se está moviendo.
IR AL VÍDEO QUE RESUELVE ESTOS CUATRO PRIMEROS APARTADOS: https://youtu.be/MYb87vVueds
e.- Hallar la distancia que ha tenido que recorrer Draco, intentando obtener una explicación a todo este follón sorprendente de tiempos, masas y distancias diferentes.
IR AL VÍDEO QUE RESUELVE ESTE ÚLTIMO APARTADO: https://youtu.be/Vs6zuBhsMos
EJERCICIO F2BE2220:
Un voluntario, con muy poca Competencia Básica en Ciencia y Tecnología, que se ha ofrecido a medir los efectos que en la salud producen los viajes espaciales a alta velocidad, se sorprende de que al regreso de la misión, en la Tierra han transcurrido 20 días, mientras que en el reloj de a bordo y en el calendario que él mismo llevó durante el viaje, sólo han pasado 18 días. Por ello está al borde de un ataque de nervios.
La situación se complica porque al comprobar su peso en la báscula de la nave, mientras realizaba el viaje, observa que tiene un peso de 96 kg (tener en cuenta que en realidad debería decir una masa de 96 kg, pero no tiene la competencia científica), lo que le parece una pasada y piensa reclamar daños por alimentación inapropiada durante el viaje.
a.- Tranquilizar al viajero, con argumentación suficiente, apoyándose en las Leyes y Teorías Físicas correspondientes.
b.- Hallar la velocidad que llevó la nave durante la misión, suponiendo que la misma fue constante en todo el viaje.
c.- Indicarle, con los razonamientos apropiados, el peso (la masa) que en realidad tiene el viajero.
d.- Hallar la longitud de la nave que se percibe desde un observador situado en la Tierra, mientras realiza el viaje, sabiendo que cuando se construyó midió 149 metros.
e.- Hallar la distancia que recorrió la nave y plantearse si coincide con la que mediría el viajero.
DATO: c=3·108 m/s
VÍDEO QUE RESUELVE ESTE EJERCICIO: https://youtu.be/yoA72M1_uY4
EJERCICIO F2BE2221:
La nave estelar, USS Enterprise mide 288,77 metros de longitud (así aparece en los planos de sus constructores).
Los sistemas de detección por radar del planeta Andoria, miembro de la Federación, indican que cuando la notaron pasar, medía 200 metros de longitud.
Explicar a qué es debida esta desviación en la medida y calcular si ello fuera posible, la velocidad de la nave al pasar por Andoria. DATO: c = 3·108 m/s.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/t9Xo1r7rDh0
EJERCICIO F2BE2484:
Un tren de supervelocidad, sostenido por levitación magnética mide 500 metros en reposo y tiene 10 vagones exactamente iguales. Este tren pasa junto a otro tren del mismo modelo en reposo.
El conductor del tren en reposo, cuando ve pasar al tren percibe por el tamaño del tren en movimiento, que parece que sólo tiene 9 vagones.
a.- ¿Cómo se explica esto?
b.- ¿ A qué velocidad se mueve el tren?
DATO: c=3·108 m/s
INDICACIONES PARA RESOLVERLO:
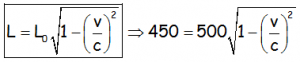
SOLUCIÓN: v=1,38E8 m/s
EJERCICIO F2BE2485:
Los muones, que se forman a unos 9 km de la superficie de la Tierra y comienzan a viajar a una velocidad del 99,78% de la velocidad de la luz, a pesar de tener un tiempo de vida de 2,2 μs, se detectan en la superficie de la Tierra. ¿Cómo es esto posible?. DATO: c=3·108 m/s
LA SOLUCIÓN CON DETALLE PUEDE ENCONTRARSE EN: UNA CONFIRMACIÓN DE LA TEORÍA DE LA RELATIVIDAD. LA VISITA DE LOS MUONES A LA SUPERFICIE DE LA TIERRA.
EJERCICIO F2BE2486. DE MASAS Y ENERGÍAS RELATIVISTAS, CUANDO NOS MOVEMOS A VELOCIDADES PRÓXIMAS A LA DE LA LUZ:
La energía relativista total de un cuerpo es la suma de su energía cinética y su energía en reposo:
E = Ec + Eo
E = m · c2
Eo = mo · c2
Donde m es la masa relativista (expresión de Lorentz) y m0 es la masa en reposo del cuerpo. La masa relativista y la masa en reposo coinciden cuando el cuerpo se mueve a velocidades muy inferiores a la velocidad de la luz, pero tiende a infinito cuando su velocidad se aproxima a c.
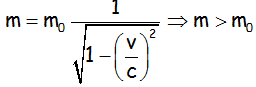
a.- Teniendo en cuenta la masa del electrón en reposo, hallar la velocidad que ha alcanzado un electrón en el acelerador de partículas, si su masa se ha hecho 15 veces mayor.
b.- Hallar la energía relativista del electrón. [E = m·c2]
c.- Hallar el valor de la energía cinética ganada por el electrón. [Ec = E – Eo]
d.- Hallar la energía cinética del electrón, según la fórmula clásica. [Ec = 1/2 m·v2, que no es lo correcto, ya que se mueve a velocidades próximas a la de la luz. Lo correcto es la diferencia entre su energía relativista total y su energía en reposo]
DATO: me=9,11E-31 kg; c=3E8 m/s
SOLUCIONES: 0,998·c m/s; 1,23E-12 J; 1,15E-12 J; 6,11E-13 J
EJERCICIO F2BE2567:
Un protón se acelera como consecuencia de aplicarle una diferencia de potencial de 3·106 V.
a.- Hallar la velocidad que alcanza el protón.
b.- Hallar la masa relativista del protón acelerado.
c.- ¿Es este protón acelerado de tipo relativista?.
d.- Hallar la longitud de onda de De Broglie del protón.
DATOS: h=6.63E-34 J·s; mp=1,6605·10-27 kg; qp=1,6·10-19 C; c=3·108 m/s
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN FINAL FÍSICA 2º BACHILLERATO. EFECTO FOTOELÉCTRICO, ONDAS, ELECTROMAGNETISMO, GRAVITACIÓN, RELATIVIDAD, CUÁNTICA.
EJERCICIO F2BE2489: EJ 16 DE ACT 99
Considere una superficie metálica de Níquel, perfectamente pulida, para la que el trabajo de extracción vale 5,36 eV. Se ilumina esta superficie con una luz monocromática y se observa que la velocidad máxima de los electrones emitidos es de 5·106 m/s. Calcular:
a.- La frecuencia umbral del metal.
b.- La frecuencia y la longitud de onda de la luz incidente.
c.- La longitud de onda de De Broglie de los electrones emitidos.
d.- La masa relativista de los electrones emitidos.
d.1.- ¿Son estos electrones de tipo relativista?
DATOS: h=6.63E-34 J·s; c=3E8 m/s; me=9.11E-31; 1 eV=1.6E-19 J
SOLUCIONES: 1.29E15 Hz; 1.85E16 Hz; 1.62E-8 m; 1.46E-10 m;
EJERCICIO F2BE2490:
Considerar una superficie metálica de Níquel, perfectamente pulida, para la que el trabajo de extracción vale 5,36 eV. Se desea emitir electrones con una energía cinética máxima de 1,64·10-15 J. Calcular: (3 puntos)
a.- La frecuencia umbral del metal.
b.- La frecuencia que debe tener la luz incidente y su longitud de onda.
c.- La longitud de onda de De Broglie de los electrones emitidos.
d.- La velocidad de los electrones emitidos.
e.- La masa relativista de los electrones emitidos.
f.- ¿Son estos electrones de tipo relativista?
DATOS: h=6.63·10-34 J·s; c=3·108 m/s; me=9.11·10-31; 1 eV=1.6·10-19 J
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO FÍSICA 2º BACHILLERATO. ONDAS, GRAVITACIÓN Y FÍSICA MODERNA
EJERCICIO F2BE2532: (LA PARTÍCULA QUE SE MUEVE LO HACE BAJO LOS EFECTOS DE UN CAMPO MAGNÉTICO)
Un electrón entra perpendicularmente en un campo magnético uniforme de 0,3 T. La velocidad con la que entra en el sentido positivo del eje OX del sistema de referencia cartesiano habitual, la obtuvo aplicándole una diferencia de potencial de 5000 V. El campo magnético está dirigido en el sentido negativo del eje OZ. Hallar:
a.- La fuerza a la que se verá sometido el electrón una vez entra en el campo magnético, explicando en un diagrama la dirección y sentido de la misma.
b.- Explicar, argumentando con rigor, la trayectoria que sigue, obteniendo el radio de la misma y el periodo si fuera posible.
c.- Realizar un dibujo explicativo, con el rigor esperado en este nivel en el que se observe el electrón entrando horizontalmente y encontrándose con el campo magnético, que incluya en él: el dibujo de la trayectoria que sigue el electrón; el vector fuerza al que se encuentra sometido, el vector velocidad y el vector aceleración (los tres vectores en dos puntos diferentes de la trayectoria)
d.- Hallar la masa relativista del electrón, comparando con la masa en reposo del electrón, añadiendo comentarios a las diferencias observadas, tomando como base argumentativa la Teoría de la Relatividad.
DATOS: c=3·108 m/s; me-= 9,1·10-31 kg; |qe-|=1,6·10-19 C.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO Y OTROS DE INTERÉS PARA FÍSICA DE 2º DE BACHILLERATO: EXAMEN RESUELTO DE FÍSICA DE 2º DE BACHILLERATO: CAMPO ELECTROSTÁTICO, MAGNÉTICO, ONDAS, RELATIVIDAD, CUÁNTICA, ÓPTICA Y DEFECTOS DEL OJO.
PARA AMPLIAR ESTE MATERIAL, PUEDE SER DE INTERÉS LA CONSULTA DEL SIGUIENTE DOCUMENTO DE APUNTES Y EJERCICIOS DE RELATIVIDAD:
99 RELATIVIDAD V6Esperamos que el material cumpla su cometido.
PODRÍA INTERESAR LA VISITA AL SIGUIENTE ARTÍCULO DEL PROYECTO, DONDE SE DESARROLLAN LAS ASIGNATURAS DE FÍSICA Y QUÍMICA DE SECUNDARIA Y BACHILLERATO:

Comments are closed, but trackbacks and pingbacks are open.