REPASO FINAL TERCER TRIMESTRE
MATEMÁTICAS II 2º BACHILLERATO
REPASO FINAL DEL TERCER TRIMESTRE (CURSO), QUE SE ESTÁ REALIZANDO EN «EL PILAR», A LO LARGO DE ESTE FINAL DE CURSO, EN MATEMÁTICAS II, EN 2º DE BACHILLERATO:

- ANÁLISIS:
- ÁLGEBRA:
- GEOMETRÍA:
- PROBABILIDAD:
ESTE MATERIAL SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
REPASO DE ANÁLISIS:
EJERCICIO M2BE2427:
Sea f(x) = x3 + Ax2 + Bx + C. Encuentra los valores de los parámetros A, B y C para que f(0) = 2, las rectas tangentes a la gráfica de f en los puntos de abscisa x = 1 y x = 3 sean paralelas y tenga un extremo relativo en el punto x = -1 .
Ese extremo relativo, ¿es un máximo o un mínimo?
Estudia si tiene algún otro extremo relativo y determina si son máximos o mínimos.
EJERCICIO M2BE2428:
Sea f(x) la función siguiente:
![]()
Estudia los intervalos de crecimiento y decrecimiento de f, calcula sus asíntotas, y encuentra la recta tangente de la gráfica de f en el punto de abscisa x = 0. Haz una representación aproximada de la gráfica de la función f.
EJERCICIO M2BE2429:
Calcular la siguiente integral, explicando el método utilizado:
![]()
EJERCICIO M2BE2430:
Dibuja el recinto limitado por las funciones f(x) = 2x2 – 4x + 3 y g(x) = x2 – 2x + 3 y calcula el área de este recinto.
EJERCICIO M2BE2431: EBAU CANARIAS 2023
Se quiere construir una Casa de la Juventud de 240 m2 de superficie, que estará rodeada por una zona ajardinada con las dimensiones de la imagen.
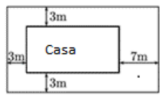
Si se quiere minimizar la superficie total de la zona ajardinada, ¿qué dimensiones debe tener la Casa de la Juventud? ¿Cuál es el área de la zona ajardinada?
IR AL ARTÍCULO QUE INCLUYE LA RESOLUCIÓN DE ESTE EJERCICIO: MATEMÁTICAS II. E.B.AU. CANARIAS 2023. EJERCICIOS RESUELTOS. CONVOCATORIA ORDINARIA JUNIO
EJERCICIO M2BE2432: EBAU CANARIAS 2012 SEPT
La temperatura T, en grados centígrados, que adquiere una pieza sometida a un cierto proceso de 6 horas de duración, viene dada en función del tiempo t transcurrido en ese proceso por la expresión:
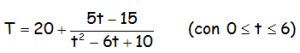
Determinar en qué momento del proceso la pieza alcanza su temperatura máxima y en qué momento alcanza su temperatura mínima. Justificar las respuestas.
EJERCICIO M2BE2433: EBAU CANARIAS 2012 SEPT
a.- Dada la función f(x) = cos2 (3x) , hallar las ecuaciones de las rectas tangente y normal a su gráfica en el punto de abscisa x=π/12 (explicar).
b.- Hallar los extremos relativos y los puntos de inflexión de la función y = 2x3 – 3x2 – 12x + 5. Justificar los resultados obtenidos.
EJERCICIO M2BE1996 (EBAU CANARIAS 2019):
Dada la siguiente expresión, de la función f de la que se desconocen algunos valores:
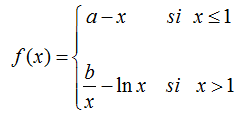
Calcular los valores de a y b para que sea derivable en todo su dominio.
Escribir la función resultante.
EJERCICIO M2BE2434:
Dada la función f(x) siguiente:
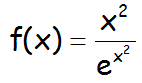
a.- Determinar los intervalos de crecimiento y los de decrecimiento (monotonía).
b.- Calcular los máximos y mínimos relativos (extremos, puntos singulares).
EJERCICIO M2BE2435:
Encontrar los dos puntos en los que se cortan las gráficas de estas dos funciones:
f(x) = 2 – 2x2 y g(x) = x4 – x2
Calcular el área de la región del plano encerrada entre ambas funciones.
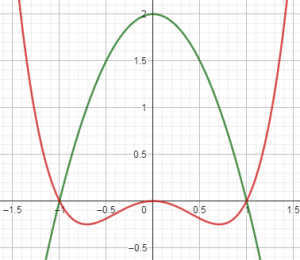
NOTA: Se debe animar al alumnado a realizar una representación completa de las dos funciones, estudiando las características adicionales principales: cortes con los ejes, máximos y mínimos. En cualquier caso, se aporta captura de geogebra:
REPASO DE ÁLGEBRA:
EJERCICIO M1BE2436:
Un número de tres cifras es tal que: la cifra de las centenas es igual a la suma de las cifras de las decenas y unidades. La diferencia entre este número y el que resulta de intercambiar las cifras de las unidades y de las centenas es 396. Hallarlo sabiendo que la diferencia entre la cifra de las decenas y la de las unidades es 2.
EJERCICIO M2BE2437:
Discutir y resolver en los casos en que sea posible, el siguiente sistema de ecuaciones, así como especificando con rigor el caso (o los casos) en que el sistema no tenga solución:
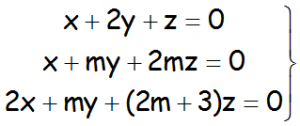
EJERCICIO M2BE2438:
Discutir y resolver en los casos en que sea posible, el siguiente sistema de ecuaciones:
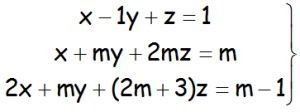
EJERCICIO M2BE2439:
Resolver las siguientes ecuaciones matriciales:
a.- XA=B
b.- AX + B = C
c.- XA + B = 2C
d.- AX + BX = C
e.- XAB – XC = 2C
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN MATRICIAL: EJERCICIO RESUELTO DE ECUACIÓN MATRICIAL, PARA MATEMÁTICAS II DE 2º DE BACHILLERATO
f.- AX – B – C = O
Siendo A, B y C las siguientes matrices:
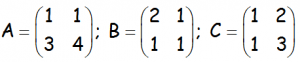
EJERCICIO M2BE2440:
Hallar la matriz X2+Y2, siendo X e Y las soluciones del siguiente sistema matricial: