MATRICES DETERMINANTES MATEMÁTICAS BACHILLERATO

MATRICES Y DETERMINANTES PARA MATEMÁTICAS DE BACHILLERATO:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

SIGUE EL PROCESO DETERMINADO POR:

- MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA

VÍDEO DE INTRODUCCIÓN DE MATRICES:

Características generales de las matrices, filas y columnas, dimensión.

Operaciones básicas: suma, resta, multiplicación por un número.

VÍDEO DE INTRODUCCIÓN DE MATRICES Y OPERACIONES BÁSICAS: https://youtu.be/lJ6jP0LABaI

EJERCICIO M2BE2042:

Realizar los siguientes productos de matrices:

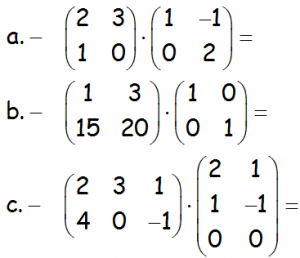
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/pVZXzrv9zCE

EJERCICIO M2BE2044:

Siendo A la matriz siguiente, hallar A².

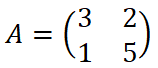
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/p_bcl7GYp-Q

EJERCICIO M2BE1959:

a.- Matriz Inversa: Definición.

b.- Hallar la matriz inversa de A, siendo A:

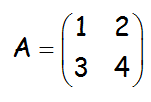
c.- Comprobar que la matriz inversa (A^-1) obtenida en el apartado anterior, realmente es la inversa de A, realizando el producto correspondiente

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/_zRORL9wjjs

EJERCICIO M2BE2039:

Hallar la matriz inversa de cada una de las siguientes matrices:

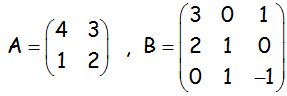
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/FUFPefZRuxM

EJERCICIO M2BE1960:

Hallar la matriz inversa de A, siendo A:

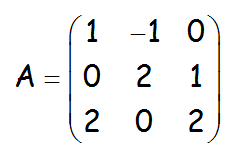
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/zHNKKOOS3vg

EJERCICIO M2BE2020:

Averigua qué dos matrices de dimensiones 3𝑥3, 𝑋 e 𝑌, verifican las siguientes
condiciones:
– La suma de ambas matrices 𝑋 e 𝑌 da como resultado la matriz 𝐼₃ (siendo 𝐼₃ la matriz identidad 3𝑥3)
– Siendo,

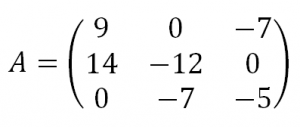
la matriz traspuesta de 𝐴 es el resultado de realizar la resta del doble de la matriz 𝑋 y cinco veces la matriz 𝑌.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/xkmMxx2ihcs

EJERCICIO M2BE1997 JL:

Siendo A y B las siguientes matrices:

¿Cuándo AB tiene inversa?

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/y6_F_id88lo

EJERCICIO M2BE2040:

Determinar los valores de los parámetros a y b para los que tiene inversa la matriz:

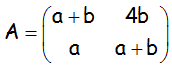
Calcular la matriz A^-1 cuando a=3 y b=1.

VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/Ohz9ZCPxCus

EJERCICIO M2BE2035:

Dadas las matrices:

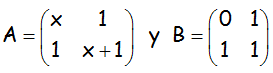
y sea I₂ la matriz identidad de orden 2,

a.- Calcular el valor de x de modo que se verifique la igualdad: B²= A

b.- Calcular el valor de x para que A – I₂= B^-1

c.- Calcular el valor de x para que A · B = I₂

VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/Tsrc7rbayg0

EJERCICIO M2BE2038:

Sean las siguientes matrices,

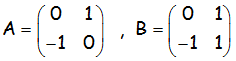
Calcular: A²⁰²⁰· X + B²⁰⁰²= A²⁰²¹

VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/EWvNE3ukQAE

EJERCICIO M2BE2037:

Hallar el rango de las siguientes matrices:

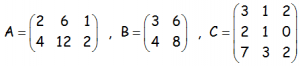
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/UagPbawZ2s8

EJERCICIO M2BE2189:

Sea a ∈ ℜ y P la matriz siguiente:

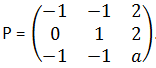
a) Calcula el determinante y el rango de P según el parámetro a.

b) Para a=1. ¿Existe la inversa? ¿Por qué? Si es posible, debes calcularla.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA DE EXAMEN DE MATEMÁTICAS II, 2º DE BACHILLERATO. ANÁLISIS, ÁLGEBRA DE MATRICES, GEOMETRÍA Y PROBABILIDAD

EJERCICIO M2BE2353:

Siendo A y B las matrices siguientes:

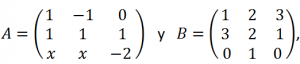
a) ¿Para qué parámetros x la matriz C=AB tiene inversa.

b) Si es posible, calcula la inversa de C cuando x=2.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ÁLGEBRA DE MATRICES

EJERCICIO M2BE3445; EBAU PAU CANARIAS JUNIO 2023:

Dadas las matrices:

a.- Comprobar si la matriz M = 2I₃ + B^t tiene inversa. Donde I₃ indica la matriz identidad de orden 3.

b.- Justificar que existe la matriz X que verifica la ecuación siguiente:

2X + C = A – X · B^t

IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIO RESUELTO M2BE3445 DE MATRICES Y ECUACIONES MATRICIALES

EJERCICIO M2BE3446; EBAU PAU CANARIAS JULIO 2024:

Dada la siguiente matriz, M_k , donde k ∈ ℜ:

a.- Estudiar el rango de la matriz M_k, dependiendo de los valores que tome el parámetro k.

b.- Tomamos M₁ como la matriz anterior para el valor k = 1 , y B la siguiente matriz:

hallar la matriz X que satisface la ecuación X · M1 + X · M₁^t = B

IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIO RESUELTO M2BE3446 DE MATRICES Y ECUACIONES MATRICIALES

EJERCICIO M2BE2210:

Sea A la siguiente matriz en la que a es un parámetro real:

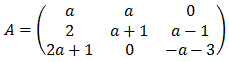
a.- Encuentra los valores de para los que la matriz A es invertible.

b.- Para a=3, resolver la ecuación matricial AX = B – 3I , donde B es la matriz:

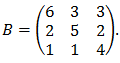
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO QUE ESTÁ INCLUÍDO EN UNA PRUEBA DE EXAMEN GLOBAL PARA MATEMÁTICAS II DE 2º DE BACHILLERATO: EXAMEN GLOBAL MATEMÁTICAS II 2º BACHILLERATO. GEOMETRÍA, ÁLGEBRA DE MATRICES, PROBABILIDAD, ANÁLISIS (OPTIMIZACIÓN)

EJERCICIO M2BE2259:

Se considera la matriz:

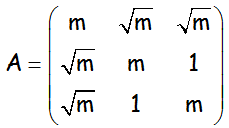
a.- ¿Para qué valores de m tiene inversa la matriz A?

b.- Para m=4 resolver, si es posible, la ecuación matricial AX = 12 I , donde I es la matriz identidad de orden 3.

IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA

EJERCICIOM2BE2956:

¿Cuándo la matriz A es regular (tiene inversa)? Si es posible, realiza la inversa para m = 2.

IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTE EJERCICIO: EXÁMENES RESUELTOS DE MATEMÁTICAS II, PARA 2º DE BACHILLERATO. ANÁLISIS DE FUNCIONES Y ÁLGEBRA. SEGUNDO TRIMESTRE 2024-25

EJERCICIO M2BE2245:

Dada la matriz A siguiente:

a.- ¿Para qué valores de a y b la matriz A no tiene inversa?

b.- Determinar la matriz inversa para el resto de valores.

IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2245 DE OBTENCIÓN DE LA MATRIZ INVERSA

EJERCICIO M2BE2378:

a.- Siendo A, B y C las siguientes matrices:

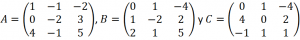
resolver la siguiente ecuación matricial: XA + C^t= – B

b.- Siendo A, B y C las siguientes matrices:

calcular x para que AB=C

c.- ¿Para qué valores de x tiene A inversa? Calcular la inversa de A en función de x.

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ÁLGEBRA DE MATRICES Y SUS APARTADOS: EXAMEN ANÁLISIS, ÁLGEBRA Y GEOMETRÍA PARA MATEMÁTICAS DE 2º DE BACHILLERATO

EJERCICIO M2BE2439:

Resolver las siguientes ecuaciones matriciales:

a.- XA=B

b.- AX + B = C

c.- XA + B = 2C

d.- AX + BX = C

e.- XAB – XC = 2C

IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN MATRICIAL: EJERCICIO RESUELTO DE ECUACIÓN MATRICIAL, PARA MATEMÁTICAS II DE 2º DE BACHILLERATO

f.- AX – B – C = O

Siendo A, B y C las siguientes matrices:

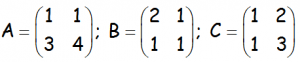
EJERCICIO M2BE2440:

Hallar la matriz X²+Y², siendo X e Y las soluciones del siguiente sistema matricial:

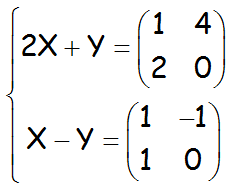
EJERCICIO M2BE2441:

Dadas las matrices A y B siguientes, se pide:

a) Calcular el determinante de A^tA.

b) Calcular el rango de BA en función de b.

c) Calcular B⁻¹ para b = 2.

d) Para b = 1, calcular B⁵.

RESOLUCIÓN PASO A PASO DEL EJERCICIO EN EL ARTÍCULO SIGUIENTE: EXAMEN TERCER TRIMESTRE MATEMÁTICAS II DE 2º DE BACHILLERATO: ANÁLISIS, ÁLGEBRA, GEOMETRÍA, PROBABILIDAD

EJERCICIO M2BE3221: PAU CANARIAS JUNIO 2025

Dada la matriz M ∈ M_2×2 , con a ∈ ℜ, siendo M, la matriz siguiente:

a.- Para cualquier valor del parámetro a: comprobar que M es invertible y dar la expresión de M^-1.

b.- Para a = -1 . calcula el valor de la matriz X que satisface la ecuación MA = B – MX, siendo A y B las siguientes matrices:

IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTE EJERCICIO: EJERCICIO RESUELTO M2BE3221 DE MATRIZ INVERSA Y ECUACIONES MATRICIALES. PAU CANARIAS JUNIO 2025

EJERCICIO M2BE3222: PAU CANARIAS JUNIO 2025

Dada la matriz A siguiente, con k ∈ ℜ:

a.- Estudiar el rango de A según los valores del parámetro k.

b.- Para k = -1, comprobar que A² = 2A – I, donde I denota la matriz identidad de orden 3. Además utilizando la igualdad anterior verifica, sin calcular la potencia, que A⁴ = 4A – 3I .

IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE3222 DE MATRICES Y ECUACIONES MATRICIALES. PAU CANARIAS JUNIO 2025

Visualizaciones: 3.874