EXAMEN MATEMÁTICAS II EXTRAORDINARIA
MATEMÁTICAS 2º BACHILLERATO CIENCIAS
EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA, REALIZADO EN «EL PILAR»:
PUEDE RESULTAR DE INTERÉS LA CONSULTA DE LOS SIGUIENTES MATERIALES DE ESTE PROYECTO DE MEJORA DEL APRENDIZAJE EN CIENCIAS:
ESTA PRUEBA SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA:
LOS EJERCICIOS DE LA PRUEBA Y SU RESOLUCIÓN PASO A PASO:
EJERCICIO M2BE2259:
Se considera la matriz:
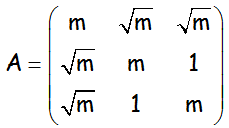
a.- ¿Para qué valores de m tiene inversa la matriz A?
b.- Para m=4 resolver, si es posible, la ecuación matricial AX = 12 I , donde I es la matriz identidad de orden 3.
RESOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M2BE2256:
Un conocido defraudador fiscal tiene distribuido su dinero negro en tres paraísos fiscales, las Islas Caimán, Panamá y Fiji.
La suma total de este dinero es de 150 millones de euros. Si perdiera la cuarta parte del dinero que tiene en las Islas Caimán, seguiría teniendo allí el triple del dinero que tiene en Panamá. Además, el dinero que tiene en Panamá sumado a las dos quintas partes del dinero que tiene en Fiji es exactamente la mitad del dinero que tiene en las Islas Caimán.
Calcule cuánto dinero tiene en cada uno de los paraísos fiscales.
RESOLUCIÓN DEL EJERCICIO:
EJERCICIO M2BE2250:
Tres de cada cinco alumnos de segundo de bachillerato de una región están matriculados en la asignatura de Matemáticas II. Se eligen 6 alumnos al azar entre todos los alumnos de segundo de bachillerato.
a) Calcular la probabilidad de que exactamente cuatro de ellos estén matriculados en Matemáticas II.
b) Es cierta la siguiente afirmación: El porcentaje de que alguno de ellos esté matriculado en Matemáticas II es superior al 99%.
c) Si en un instituto de esa región hay matriculados en segundo de bachillerato 120 alumnos, calcular la probabilidad de que más de 60 de estos alumnos estén matriculados en Matemáticas II.
RESOLUCIÓN DEL EJERCICIO:
EJERCICIO M2BE2262:
El 10% de la población de Canarias tiene alergia a la flor del olivo.
- En una muestra de 100 individuos, ¿qué probabilidad hay de que más de 12 seleccionados tengan alergia a la flor del olivo?
- Se toma una muestra de 400 individuos, ¿cuál es la probabilidad de que menos de 32 seleccionados tengan alergia a la flor del olivo?
- En una muestra de 500 individuos, ¿cuál es el número esperado de individuos que no tendrán alergia a la flor del olivo?
RESOLUCIÓN DEL EJERCICIO:
EJERCICIO M2BE2225: EBAU CANARIAS 2011
Dadas las funciones: y = – x2 + 4x e y = 2x2 – 2x
a.- Representar la región que determinan sus gráficas.
b.- Calcular el área de dicha región.
RESOLUCIÓN DEL EJERCICIO:
EJERCICIO M2BE2255:
Se considera la función:
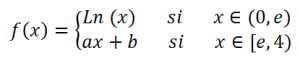
donde a y b son números reales.
Encuentre el valor de a y de b para que la función sea continua y derivable en el intervalo (0,4).
RESOLUCIÓN DEL EJERCICIO:
EJERCICIO M2BE2267: EBAU CANARIAS 2020
Consideremos la recta r siguiente:
y el plano π1 ≡ x – y + 3z = 12
a.- Calcular la ecuación del plano π2 que contiene a la recta r y es perpendicular al plano π1.
b.- Sabiendo que la recta r corta al plano π1, averigüe el punto de intersección,
RESOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M2BE2244: EBAU CANARIAS JUNIO 2014
Dados los puntos A (-1,0,3), B (2,4,1) y C (-4,3,1):
a.- Estudiar si los puntos A,B y C están alineados.
b.- Hallar la ecuación de la recta paralela al segmento AB y que pasa por C. Expresarla como intersección de dos planos.
RESOLUCIÓN DEL EJERCICIO: