CLASE ONLINE PROGRAMA REFUERZO
MATEMÁTICAS I 1º BACHILLERATO
ANÁLISIS FUNCIONES MATEMÁTICAS BACHILLERATO
CLASE ON LINE DE ANÁLISIS DE FUNCIONES PARA 1º DE BACHILLERATO. PROGRAMA DE REFUERZO DE CONTENIDOS SIGNIFICATIVOS, DEL 25 DE ABRIL DE 2024:

Clase on-line de análisis de funciones, para Matemáticas de 1º de Bachillerato de la Modalidad de Ciencias y Tecnología realizada en el Instituto «EL PILAR».
VÍDEO CON LA CLASE ON LINE DE ANÁLISIS DE FUNCIONES:
ANÁLISIS DE FUNCIONES: DERIVADAS Y APLICACIONES, INTEGRALES BÁSICAS Y APLICACIONES.
VÍDEO CON LA CLASE ONLINE: …en construcción…
La dinámica se realiza dentro del PROGRAMA DE MEJORA DEL APRENDIZAJE en MATEMÁTICAS PARA 1º DE BACHILLERATO, del Centro. Los alumnos que lo desean, fuera del horario lectivo, por la tarde, asisten a ella a través de Teams, en el equipo configurado al efecto. Se aporta aquí con la idea de que lo aprovechen incluso los que no han podido estar en tiempo real.
En la clase de hora y media de duración, de cuyo vídeo aportamos el enlace, se resuelven y se explican las siguientes cuestiones de ANÁLISIS DE FUNCIONES para este nivel de MATEMÁTICAS de 1º de BACHILLERATO.
El desarrollo de la clase, a modo de sinopsis del vídeo, ha sido el siguiente, realizando las siguientes actividades y ejercicios:
EJERCICIOS M1BE2463:
Obtener la derivada de las siguientes funciones:
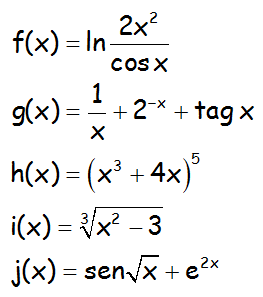
EJERCICIO M1BE2464:
Obtener la derivada de la siguiente función, utilizando la definición de derivada:
f(x) = x3 – 2x2 + 7
EJERCICIO M1BE2465:
Para la siguiente función polinómica:
f(x) = x3 + 6x2 + 5x -12
Estudiar la monotonía y la curvatura.
EJERCICIO M1BE2466:
Determine los valores de los parámetros a, b y c para que la función:
f(x) = a·(x-1)3 + bx + c
a.- Pase por el punto (1, 1).
b.- En el punto (1, 1) su tangente tenga de pendiente 2.
c.- En el punto x=2 tenga un máximo relativo.
EJERCICIO M1BE2467:
Para la siguiente función:
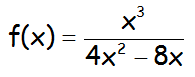
Realizar el estudio completo de las asíntotas.
EJERCICIO M1BE2468:
Hallar el área encerrada por las siguientes funciones, representando previamente el recinto correspondiente:
f(x) = x2 – 4 y g(x) = 2 – x
