ANÁLISIS FUNCIONES MATEMÁTICAS BACHILLERATO
ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO:

Este artículo debe ser considerado el artículo matriz para este contenido de funciones de 1º de bachillerato.
CONOCIMIENTO DE LAS FUNCIONES ELEMENTALES:
En este nivel de Matemáticas de Bachillerato, es necesario el conocimiento de las «siluetas» y características más significativas de los distintos tipos de funciones. Ello nos ayudará entre otras cuestiones a realizar un boceto, analizar el dominio o la obtención del límite.
CLASE ON-LINE DE INTRODUCCIÓN AL ANÁLISIS DE FUNCIONES:
FUNCIONES ELEMENTALES: https://youtu.be/jsA89Ktt5zI?si=mLrFXbgJlu7xQits
Se representan funciones lineales, utilizando la clásica tabla de valores e incluso los conceptos de la ordenada en el origen y de la pendiente para la obtención de la recta que corresponde en cada caso. Se introduce el modo de obtener los puntos de corte con los ejes. Esta primera parte se trabaja a través de las funciones:
f(x) = 4; f(x) = 3, funciones horizontales o constantes
f(x) = 2x; función lineal
f(x) = 2x + 1; f(x) = 2x + 3 , funciones afín
f(x) = – x + 1, con pendiente negativa.
Se representan funciones cuadráticas, a través de los puntos de corte con los ejes, así como obteniendo el vértice de la parábola. Se indica que el signo del coeficiente del monomio de 2º grado según sea positivo o negativo, nos da información de si la parábola es cóncava «∪» o convexa «∩».
Se trabaja con las funciones cuadráticas siguientes, que se representan según nos indica lo descrito anteriormente:
f(x) = x2 – 3x;
f(x) = – x2 – 2x + 8; que además se contrastan con la aplicación geogebra , obteniendo incluso con las herramientas que suministra de vértice y puntos de corte.
Se aprovecha la aplicación geogebra para contrastar las funciones lineales que se trabajaron inicialmente.
Se representa con detalle la siguiente función a trozos, se contrasta con geogebra y se comenta la continuidad. Se indica además, a través de la representación, la imagen o el recorrido de la función, así como el dominio.
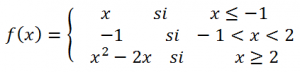
Se trabaja con la siguiente función racional, estudiando el dominio en un primer momento.
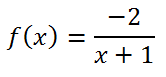
Se confirma la presencia de asíntota vertical introduciendo el concepto de límite a la izquierda y a la derecha de ese lugar posible de asíntota vertical, analizando la tendencia de la función a cada lado de la asíntota.
Del mismo modo e introduciendo el concepto de límite en el infinito se confirma la presencia de asíntota horizontal en el infinito. Del mismo modo con el menos infinito.
Todas estas cuestiones se contrastan con la representación a través de geogebra.
Se estudia y representa esta nueva función a trozos, igualmente con su contraste con geogebra:
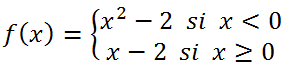
EN CUALQUIER CASO, EL ACCESO A LAS CLASES DE REFUERZO DE MATEMÁTICAS I DE 1º DE BACHILLERATO, REALIZADAS EN EL PILAR.
EJERCICIO M1BE2151:
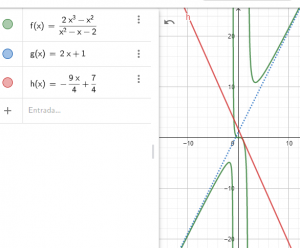
Relacionar cada una de las expresiones de las siguientes funciones con su representación gráfica:
EJERCICIO M1BE2151 FUNCIONES ELEMENTALES okFUNCIONES PERIÓDICAS:
No podemos dejar atrás a las funciones trigonométricas, por su importancia en física en los movimientos armónicos y en general en los movimientos ondulatorios.
EJERCICIO M1BE2152:
Identificar en la imagen siguiente las funciones seno, coseno y tangente, notando con lo que sabemos de los valores de las razones trigonométricas, los valores de las tres funciones para 0º, 90º, 180º, 270º, 360º. Hacer comentarios acerca de la continuidad de cada una de las funciones y de la periodicidad:
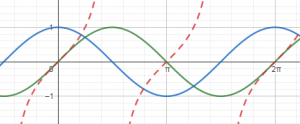
MUY RECOMENDABLE EL ACCESO AL SIGUIENTE MATERIAL:
LAS FUNCIONES TRIGONOMÉTRICAS SENO Y COSENO. COMO LA VIDA MISMA
DOMINIOS DE FUNCIONES:
EJERCICICIO M1BE2153:
Estudiar el dominio de las siguientes funciones:
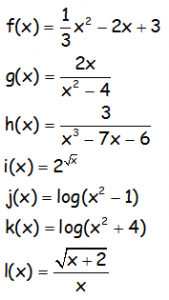
EJERCICIO M1BE2154:
Estudiar el dominio de las siguientes funciones:
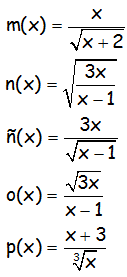
EJERCICIO M1BE2303:
Calcula el dominio de la siguiente función:
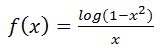
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: PROPUESTA DE EVALUACIÓN FUNCIONES 1º BACHILLERATO
EJERCICIO M2BE2012:
Estudiar el dominio de las siguientes funciones,
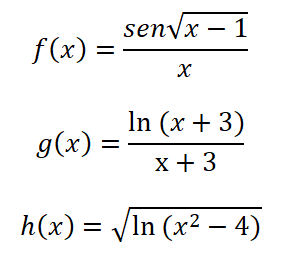
VÍDEO QUE RESUELVE EL ÚLTIMO DOMINIO: https://youtu.be/cC5UsrLQb0g
EJERCICIO M1BE2174:
Calcula el dominio de las siguientes funciones de forma argumentada:
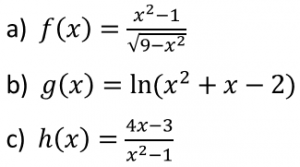
IR AL ARTÍCULO QUE TIENE LA RESOLUCIÓN DEL EJERCICIO: PRUEBA DE EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO
EJERCICIO M1BE2216:
Calcular el dominio de la siguiente función:
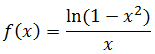
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO
EJERCICIO FQ1BE2407:
Indicar el dominio de la siguiente función, que debe argumentarse,
![]()
IR AL ARTÍCULO CON LA CLASE ONLINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
EJERCICIO FQ1BE2408:
Indicar el dominio de la siguiente función, que debe argumentarse,
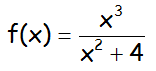
IR AL ARTÍCULO CON LA CLASE ONLINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
EJERCICIO FQ1BE2409:
Indicar el dominio de la siguiente función, que debe argumentarse,
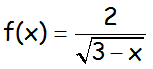
IR AL ARTÍCULO CON LA CLASE ONLINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
EJERCICIO FQ1BE2410:
Indicar el dominio de la siguiente función, que debe argumentarse,
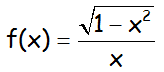
IR AL ARTÍCULO CON LA CLASE ONLINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
FUNCIONES A TROZOS:
No todos los comportamientos que se describen mediante funciones se mantienen estables durante todo el rango del estudio. Si estudiamos el crecimiento de una población de bacterias a lo largo del tiempo, podemos imaginar que al principio el crecimiento será exponencial, como consecuencia de la mitosis. Posteriormente tenderá a estabilizarse debido a la disminución del alimento y a largo plazo puede incluso decaer la población como consecuencia de la eliminación del alimento del medio e incluso por causa de las propias excreciones de las bacterias. Cuando un comportamiento (biológico, social, económico…) tiene tendencias diferentes en distintos momentos, para estudiar esa realidad necesitamos funciones a trozos.
EJERCICIO M1BE2155: de la introducción a la continuidad de funciones.
Representar la siguiente función a trozos f(x):
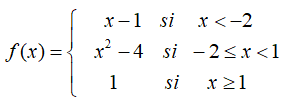
Haciendo los cálculos necesarios, prestando especial atención a los puntos de corte con los ejes, obteniendo vértices en caso de parábolas e indicando la continuidad de la función.
EJERCICIO M1BE2156: de la introducción del concepto de límite.
Para la siguiente función, que debe representarse:
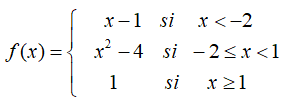
Responder de manera razonada e intuitivamente y a la vista de la representación a las siguientes cuestiones:
a.- ¿A qué valor tiende la función cuando la x tiende a infinito?*
b.- ¿A qué valor tiende la función cuando la x tiende a menos infinito?*
*En matemáticas, a eso se le llama límite de la función
c.- ¿Cuál es el límite de la función cuando x tiende a cero?.
d.- ¿Cuál es el límite de la función cuando x tiende a -2?
e.- ¿Cuál es el límite de la función cuando x tiende a 1?
f.- ¿En algún caso coincide el límite con el valor de la función en el punto? (indicarlo).
g.- ¿En qué puntos dirías que la función «no tiene límite»?
EJERCICIO M1BE2157:
a.- Representar la siguiente función:
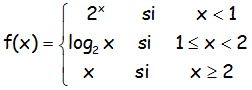
b.- Hallar los siguientes límites, contrastando los resultados obtenidos analíticamente con la representación gráfica e indicando cuando sea necesario los límites laterales:
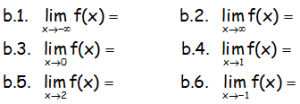
c.- Hallar: f(-1); f(0); f(1); f(2)
d.- Indicar la continuidad de la función f(x).
EJERCICIO M1BE2179: REPRESENTACIÓN EN GEOGEBRA DE UNA FUNCIÓN A TROZOS
Para la siguiente función, REALIZAR LA REPRESENTACIÓN EN GEOGEBRA:
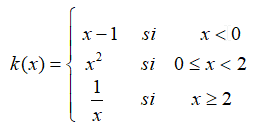
VÍDEO CON LA FORMA DE HACERLO: https://youtu.be/rRlGc3nNeMU
ACCESO A OTROS TUTORIALES DE GEOGEBRA RELACIONADOS: UTILIZACIÓN DE GEOGEBRA EN MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO.
CONTINUIDAD DE FUNCIONES:
- DEFINICIÓN DE CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO
- CLASIFICACIÓN Y TIPOS DE DISCONTINUIDADES DE UNA FUNCIÓN
- CONTINUIDAD DE ALGUNAS FUNCIONES ELEMENTALES
LÍMITES DE FUNCIONES:
LÍMITES PARA MATEMÁTICAS DE BACHILLERATO
EJERCICIOS M1BE2158:
EJERC CALCULO LIMITES 1BACEJERCICIOS M1BE2388:
Ejercicios trabajados en la clase de refuerzo: CLASE DE REFUERZO DE CÁLCULO DE LÍMITES PARA MATEMÁTICAS DE 1º DE BACHILLERATO EN «EL PILAR»
EJERCICIOS M1BE2388 LÍMITES 1º BACHILLERATO
EJERCICIO M1BE2175:
Calcular los siguientes límites de forma argumentada:
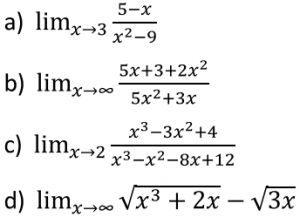
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: PRUEBA DE EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO
EJERCICIO M1BE2172:
Para la siguiente función, f(x), definida a trozos del siguiente modo:
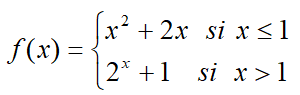
a.- Representarla con rigor y obteniendo los puntos significativos correspondientes.
ESTUDIO GRÁFICO:
b.- Con la representación, indicar la continuidad de la función.
c.- Con la representación indicar los siguientes límites:
c.1.- Límite cuando x tiende a 1, especificando los laterales.
c.2.- Límite cuando x tiende a cero.
c.3.- Límite cuando x tiende a infinito.
c.4.- Límite cuando x tiende a menos infinito.
d.- A través de la representación indicar el valor de f(1)
ESTUDIO ANALÍTICO, que debe coincidir con lo obtenido gráficamente:
e.- Con la expresión analítica de la función y realizando los cálculos adecuados a través de la definición de continuidad de una función en un punto, indicar la continuidad de la función f(x).
f.- Con la expresión analítica de la función, hallar los siguientes límites:
f.1.- Límite cuando x tiende a 1, especificando los laterales.
f.2.- Límite cuando x tiende a cero.
f.3.- Límite cuando x tiende a infinito.
f.4.- Límite cuando x tiende a menos infinito.
g.- A través de la expresión analítica indicar el valor de f(1)
EJERCICIO M1BE2176:
De la siguiente función a trozos f(x):
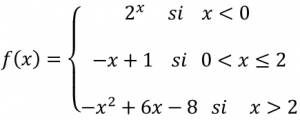
a) Representarla.
b) Indicar el dominio y el recorrido de la función.
c) Indicar la monotonía de la función.
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: PRUEBA DE EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO
EJERCICIO M2BE1826:
Hallar el siguiente límite:
EJERCICIO M2BE1827:
Hallar el siguiente límite:
EJERCICIO M2BE1828:
Hallar el siguiente límite:
IR A LA RESOLUCIÓN DE ESTOS TRES ÚLTIMOS LÍMITES
EJERCICIO M2BE2276 A:
Calcular el siguiente límite:
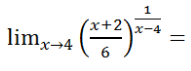
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24
EJERCICIO M2BE2276 B:
Calcular el siguiente límite:
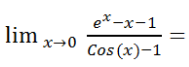
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24
EJERCICIO FQ1BE2412:
Realizar el siguiente límite
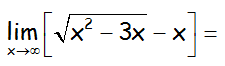
IR AL ARTÍCULO CON LA CLASE ON LINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
EJERCICIO FQ1BE2413:
Realizar el siguiente límite
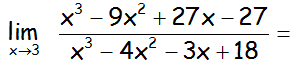
IR AL ARTÍCULO CON LA CLASE ON LINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
ASÍNTOTAS. APLICACIONES DE LOS LÍMITES:
ASÍNTOTAS VERTICALES:
La condición de presencia de una asíntota vertical en una función f(x):
![]()
Haremos este límite, y si el resultado es infinito, la función presenta una asíntota vertical de ecuación x=a.
Los posibles valores de a en los que debemos plantearnos la posibilidad de Asíntota Vertical son:
-
-
- Los valores que anulen el denominador en las funciones racionales, igualando el denominador a cero.
- Cuando tenemos funciones logarítmicas del tipo log[f(x)], aquellos valores en los que f(x)=0, ya que el logaritmo de cero tiende a -∞
- Cuando tenemos funciones del tipo tg[f(x)], aquellos valores en los que f(x)=π/2+kπ. Tengamos en cuenta que la tangente de 90º y 270º son ∞ y -∞ respectivamente.
- El estudio completo consiste en calcular los límites por la derecha e izquierda del punto a, y fijarse en el signo del infinito que resulta, de tal manera que ésa será la tendencia a ambos lados de la asíntota vertical, lo cual además aporta muchísima información a la hora de representar la función.
-
ASÍNTOTAS HORIZONTALES:
![]()
El estudio completo consiste en calcular el límite cuando x tiende a infinito y a menos infinito, ya que la asíntota puede ser diferente a cada lado e incluso no tener en uno de ellos. Esto último es sobre todo interesante en funciones con radicales, exponenciales y otras complicadas.
Además se suele calcular la POSICIÓN DE LA CURVA CON RESPECTO A LA ASÍNTOTA, dato que se obtiene calculando el signo de la diferencia entre la función y la asíntota, teniendo en cuenta que es un razonamiento para valores grandes de la variable con el signo que corresponda.
Si el signo de [f(x)-k] es positivo, es la curva la que está por encima de la asíntota, y si es negativo es la asíntota la que está por encima.
ASÍNTOTAS OBLICUAS:
f(x) presenta una asíntota oblicua de ecuación y=mx+n si tanto m como n tienen sentido (dan números finitos) calculados de la siguiente forma:
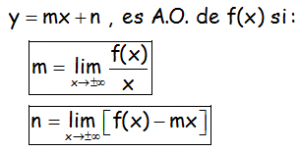
Como es posible que sean diferentes las asíntotas oblicuas hacia la derecha y hacia la izquierda hay que calcular estos límites cuando x tiende a infinito y cuando x tiende a menos infinito.
El estudio completo también requiere el conocimiento de la posición de la curva con respecto a la asíntota que se sabe calculando el signo de [f(x)-(mx+n)] para valores grandes de x (sustituyendo por ejemplo por x=1000); si da positivo, la función está por encima de la asíntota, si negativo, la función está por debajo.
Posiblemente pueda resultar interesante consultar el artículo RAMAS PARABÓLICAS.
Así como LA ASÍNTOTA HORIZONTAL ES UN CASO PARTICULAR DE OBLICUA, que concreta más acertadamente la expresión: «si una función tiene asíntota horizontal, no tiene oblicua.»
EJERCICIOS M1BE2178:
Realizar el estudio completo de las asíntotas de las siguientes funciones, realizando un boceto de las mismas utilizando la información obtenida e incluso alguna otra que se considere relevante (corte con los ejes, dominio…). Contrastar lo obtenido analíticamente con la representación gráfica, utilizando geogebra:
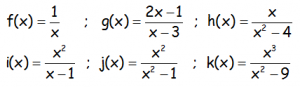
EJERCICIO M1BE2217:
Teniendo en cuenta la siguiente función:
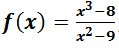
Obtener:
a.- Asíntotas.
b.- Cortes con los ejes.
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO
EJERCICIO M1BE2472:
Calcular las asíntotas de la siguiente función, argumentando matemáticamente todo el proceso que se realiza:
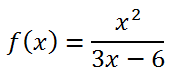
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
DERIVADAS Y APLICACIONES:
- Derivada: DEFINICIÓN DE DERIVADA
- INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA
- Ejercicios Resueltos de OBTENCIÓN DE LA DERIVADA UTILIZANDO LA DEFINICIÓN
EJERCICIO M1BE1969: UTILIZACIÓN DE LA DEFINICIÓN DE DERIVADA
Obtener la derivada de la función: f(x)=x2+3x+1 , utilizando la definición de derivada.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/-So0Dr2frY4
EJERCICIO M1BE2193:
Utilizando la definición de derivada, obtener la derivada de las siguientes funciones:
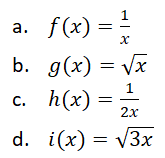
EJERCICIO M1BE2304:
Calcula la derivada de f(x) = 2x2+1 , utilizando la definición de derivada.
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: PROPUESTA DE EVALUACIÓN FUNCIONES 1º BACHILLERATO
CÁLCULO DE DERIVADAS, DE INTRODUCCIÓN DEL CONCEPTO, PROPIEDADES BÁSICAS Y CÁLCULO DE DERIVADAS DE TIPO POTENCIAL:
MÁS RECURSOS AUDIOVISUALES DE OBTENCIÓN DE DERIVADAS:
EJERCICIO M1BE2473:
Utilizando la definición de derivada, obtener la derivada de la siguiente función:
f(x) = 3x2 + 5x
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
TABLA DE DERIVADAS PROPUESTA:
TABLA DERIVADASPROPUESTA DE EJERCICIOS PARA CALCULAR LA DERIVADA:
EJERCICIOS CALCULO DERIVADAS MATEMATICAS I BACHILLERATOEJERCICIOS M1BE2200:
Hallar la derivada de las siguientes funciones.
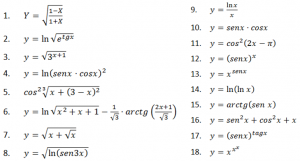
EJERCICIO M1BE2219:
Calcular y simplificar las siguientes derivadas:
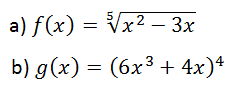
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO
EJERCICIO M1BE2220:
Calcular y simplificar las siguientes derivadas:
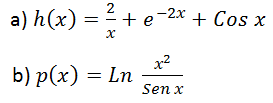
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO
EJERCICIO M1BE2306:
Calcular las siguientes derivadas, simplificándolas al máximo posible:
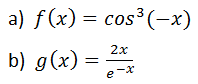
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: PROPUESTA DE EVALUACIÓN FUNCIONES 1º BACHILLERATO
EJERCICIO FQ1BE2411:
Realizar la derivada de la siguiente función
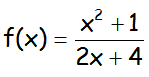
IR AL ARTÍCULO CON LA CLASE ON LINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
EJERCICIO M1BE2469:
Obtener la derivada de la siguiente función:
![]()
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
EJERCICIO M1BE2470:
Obtener la derivada de la siguiente función:
![]()
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
EJERCICIO M1BE2471:
Obtener la derivada de la siguiente función:
![]()
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
CUANDO CALCULAMOS Y OBTENEMOS UNA DERIVADA, CON FRECUENCIA DUDAMOS SOBRE LA EXPRESIÓN FINAL CORRECTA. LA EXPRESIÓN DEBE ESTAR SIMPLIFICADA, CUANDO ELLO SEA POSIBLE Y EN CUALQUIER CASO DEBE RESPONDER A LAS NORMAS FORMALES SOBRE LAS EXPRESIONES FINALES MATEMÁTICAS. PARA ESTO ÚLTIMO PUEDE RESULTAR RECOMENDABLE LA CONSULTA DEL ARTÍCULO: ARITMÉTICA PARA 1º DE BACHILLERATO.
EJERCICIO M1BE2203:
Recordando que los logaritmos son tus amigos a la hora de derivar, hallar la derivada de las siguientes funciones:
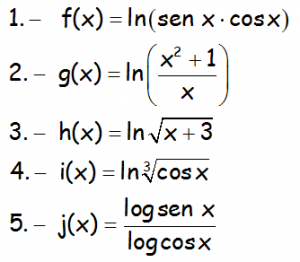
DERIVADAS EN FÍSICA:
La derivada es variación. Los conceptos que se trabajan en física en bachillerato, pueden servir para intentar entender la importancia de la derivada como herramienta matemática aplicada en Física. Les proponemos el siguiente material audiovisual, que puede ser de interés para ver la utilidad de esta herramienta.
EJERCICIO M1BE2181:
Para la siguiente función: f(x) = x2 – 2x – 3
a.- Hallar la derivada utilizando la definición.
a.1.- Intentar reconocer las rutinas iniciales o «trucos» para derivar polinomios.
b.- Con la derivada, hallar el vértice.
c.- Obtener los cortes.
d.- Reflexionar sobre la curvatura, comparándola con f(x) = -x2 – 2x – 3
e.- Contrastarla con la representación gráfica.
EJERCICIO M1BE2182:
Para las siguientes funciones:
f(x) = x2 – 6x + 8
g(x) = x3 – 3x2
h(x)= x3 – 6x
a.- Obtener la derivada utilizando la definición, intentando descubrir las rutinas o «trucos» de la operación.
UNA VEZ OBTENIDA LA DERIVADA:
Hacer una interpretación de la operación, que no es sino «variación*» (en mates «de y respecto de x» y en física lo más frecuente «de algo respecto del tiempo»), utilizando para obtener del MRUA y del MRU la velocidad a través de la ecuación del movimiento y la aceleración a través de la velocidad en los dos casos.
*variación=inclinación=pendiente de la recta tangente
CON LA DERIVADA Y LA REPRESENTACIÓN EN GEOGEBRA DE LA FUNCIÓN, PARA OBSERVAR EXTREMOS, MONOTONÍA Y CURVATURA, RELACIONÁNDOLOS CON LOS VALORES DE LA DERIVADA:
b.- Identificar los máximos o mínimos, ya que son los puntos en los que la derivada se anula (la recta tangente no tiene pendiente).
c.- Indentificar los intervalos de crecimiento y decrecimiento (la monotonía), ya que cuando la derivada es positiva (recta tangente con pendiente hacia arriba) la función es creciente y cuando es negativa (recta tangente con pendiente hacia abajo) la función es decreciente.
d.- Derivando la derivada, intentar descubrir el signo de la segunda derivada que corresponde para cada curvatura característica (cóncavo-convexo), así como donde se presenta un punto de inflexión (ni cóncavo ni convexo).
AL TERMINAR LA CLASE Y EL EJERCICIO, HEMOS VISTO CON GEOGEBRA Y LAS DOS FUNCIONES:
- La derivada de una función en un punto coincide con la pendiente de la recta tangente en ese punto.
- Por lo anterior, si una función es creciente en un punto, su derivada es positiva; y si es decreciente en ese punto, su derivada es negativa.
- En los máximos, ocurre que la función pasa de creciente a decreciente.
- En los mínimos la función pasa de decreciente a creciente.
- Para estudiar la monotonía se localiza el/los punto/s donde la derivada vale cero (máximo o mínimo), que delimita/n intervalos, donde se estudia el crecimiento y decrecimiento.
- Con respecto a la derivada de la derivada: si la segunda derivada es positiva, nos encontramos en tramos de curva convexa; si es negativa, tramos cóncavos. Si la segunda derivada es cero, tendremos un punto de inflexión, donde la función no es ni cóncava ni convexa, o lo que es lo mismo, pasa de cóncava a convexa o a la inversa.
EN RESUMEN:
- Si en xo la función tiene un MÁXIMO:
- f´(x0) = 0; f´´(x0) < 0
- Si en x0 la función tiene un MÍNIMO:
- f´(x0)=0; f´´(x0)<0
- Si en xo la función es CRECIENTE:
- f´(x0)>0
- Si en x0 la función es DECRECIENTE:
- f´(x0)<0
- Si en x0 la función es CÓNCAVA «∪»:
- f´´(x0)<0
- Si en x0 la función es CONVEXA «∩»:
- f´´(x0)>0
- Si en x0 la función no es ni cóncava ni convexa (PUNTO DE INFLEXIÓN):
- f´´(x0)=0
EJERCICIO M1BE2183: (FUNCIÓN POLINÓMICA 2 JL)
Para la función: f(x) = x3 – 2x2 – 9x + 18, hallar:
a.- Puntos de corte con los ejes.
b.- Extremos relativos.
c.- Puntos de inflexión.
d.- Indicar la monotonía.
e.- Indicar la curvatura.
f.- Representar la función, manualmente con lo obtenido y con geogebra, realizando el contraste.
REPRESENTACIÓN DE FUNCIONES:
PASOS PARA LA REPRESENTACIÓN DE FUNCIONES PARA MATEMÁTICAS DE BACHILLERATO:
-
-
- PERIODICIDAD
- En casos de funciones trigonométricas
- PERIODICIDAD
-
-
- DOMINIO
- CONTINUIDAD
- PUNTOS DE CORTE CON LOS EJES. Con Eje OX y con eje OY
- SIGNO DE LA FUNCIÓN
- SIMETRÍAS Respecto al eje OY y respecto al Origen
- CRECIMIENTO Y DECRECIMIENTO DE LA FUNCIÓN (MONOTONÍA)
- MÁXIMOS Y MÍNIMOS
- CONCAVIDAD Y CONVEXIDAD (CURVATURA)
- PUNTOS DE INFLEXIÓN
- ASÍNTOTAS Y RAMAS PARABÓLICAS Verticales, horizontales y oblicuas
- REPRESENTAR LA FUNCIÓN
-
-
-
- Una vez obtenida analíticamente de la función todas la información anterior, se trata de representarla, de hecho es el objetivo final. Sin un criterio absoluto, se recomienda:
- En los ejes cartesianos representar por este orden:
- Los puntos de corte
- Los puntos máximos, mínimos o de inflexión.
- Las asíntotas (verticales, horizontales u oblícuas)
- Una vez hecho esto, atreverse a representar la silueta de la función que pase por esos puntos y respete la presencia de las asíntotas y comprobar que cumple el resto de la información obtenida: continuidad, crecimiento, decrecimiento, concavidad, convexidad o simetrías. Si no responde modificarla al caso. El mejor consejo posiblemente sea atreverse a hacer una representación y contrastar, y así hasta que todo cuadre.
- Una vez obtenida analíticamente de la función todas la información anterior, se trata de representarla, de hecho es el objetivo final. Sin un criterio absoluto, se recomienda:
-
-
EJERCICIO M1BE2079:
Realizar el estudio completo de la siguiente función y representarla. Contrastar la representación utilizando Geogebra para Ipad o similar:
f(x) = x3 – 3x + 2
EJERCICIO M1BE2080:
Realizar el estudio completo de la siguiente función y representarla. Contrastar la representación utilizando Geogebra para Ipad o similar:
f(x) = x3 + x2 – 6x
EJERCICIO M1BE2081:
Realizar el estudio completo de la siguiente función y representarla. Contrastar la representación utilizando Geogebra para Ipad o similar:
f(x) = x3 + 3x2 + 3x + 1
EJERCICIO M1BE2082:
Realizar el estudio completo de la siguiente función y representarla. Contrastar la representación utilizando Geogebra para Ipad o similar:
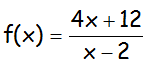
EJERCICIO M1BE2083:
Realizar el estudio completo de la siguiente función y representarla. Contrastar la representación utilizando Geogebra para Ipad o similar:
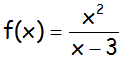
EJERCICIO M1BE2084:
Realizar el estudio completo de la siguiente función y representarla. Contrastar la representación utilizando Geogebra para Ipad o similar:
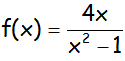
EJERCICIO M1BE2405:
Representar la función:
f(x) = x3 – x2 – x + 1
Obteniendo el dominio, puntos de corte con los ejes, extremos y monotonía. puntos de inflexión y curvatura, simetrías.
IR AL ARTÍCULO CON LA CLASE ON LINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
EJERCICIO FQ1BE2406:
Representar la siguiente función, obteniendo el dominio y las asíntotas.
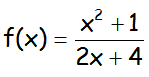
IR AL ARTÍCULO CON LA CLASE ON LINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO
EJERCICIO M1BE2218:
Siendo f(x) = 2x3 – 5x2 – 4x , realizar los siguientes apartados:
a.- Monotonía y máximos y mínimos.
b.- Curvatura y puntos de inflexión.
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO
EJERCICIO M1BE2420:
Representar la siguiente función polinómica, f(x) = x3 + 2x2 – x – 1, obteniendo previamente todo lo que resulte significativo. Realizar posteriormente el contraste con geogebra.
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: TRABAJO TRIMESTRAL DE REPRESENTACIÓN DE FUNCIONES PARA MATEMÁTICAS I DE 1º BACHILLERATO
EJERCICIO M1BE2474:
Para la siguiente función polinómica, f(x) = x3 + 3x2 – 4x , calcular:
a.- La monotonía y los extremos relativos.
b.- La curvatura y los puntos de inflexión.
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
EJERCICIO M1BE2004:
Considera la función:
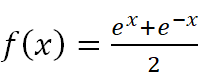
a) Estudia y determina los intervalos de crecimiento y los intervalos de decrecimiento de f. Calcula los extremos relativos de f (abscisas donde se obtienen y valores que se alcanzan).
b) Halla la ecuación de la recta normal a la gráfica de f en el punto de abscisa x = 0.
EJERCICIO M2BE2277:
Dada la siguiente función f(x):
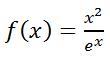
a.- Determinar los intervalos de crecimiento y los de decrecimiento.
b.- Calcular los máximos y mínimos relativos.
IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24
EJERCICIO M1BE2305:
Para la función f(x) que se añade, realizar los siguientes apartados:
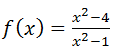
a) Dominio.
b) Asíntotas.
c) Cortes con los ejes.
d) Monotonía y extremos relativos.
e) Representar la función.
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: PROPUESTA DE EVALUACIÓN FUNCIONES 1º BACHILLERATO
EJERCICIO M1BE2187:
Estudiar las siguientes funciones, obteniendo todo lo que sea posible y representarlas con la información obtenida:
Se recomienda el contraste con geogebra
a. f(x) = (x-2)(x-1)(x+1)
b.- g(x) = x3 + x2
c.- h(x) = x3 – 2x2 + x
d.- i(x) = x3 – 6x2 + 9x
e.- j(x) = (x+1)3
f.- k(x) = -x4 + 2x2
g.- l(x) = x4 – 4x2
EJERCICIOS M1BE2199:
Estudiar las siguientes funciones, obteniendo todo lo que sea posible y representarlas con la información obtenida:
Se recomienda el contraste con geogebra
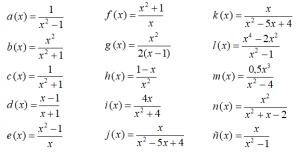
EJERCICIO M1BE2015:
Para la siguiente función:
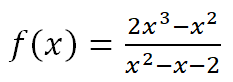
a.- Estudiar el dominio de definición y calcule las asíntotas horizontales, verticales y oblicuas caso de existir.
b.. Calcular la recta tangente a la curva en el punto x=1
EJERCICIO FQ1BE2549, TAREA INTERDEPARTAMENTAL MAT/FYQ:
Sabemos que en un oscilador armónico, cuerpo que se mueve con un movimiento armónico simple, en ausencia de rozamientos, se conserva la energía mecánica, que es igual a la suma de la energía cinética y la energía potencial:
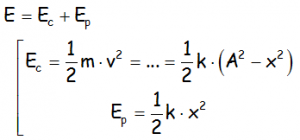
Para un movimiento armónico, cuyas expresiones de la energía cinética y la potencial en función de la posición responde a: Ec(x) = 10 – 2,5 x2 ; Ep(x) = 2,5 x2 . Para una partícula de 25 g de masa que vibra según se indica, responder a las siguientes cuestiones:
a.- Identificar la amplitud del movimiento.
b.- Localizar analíticamente los puntos de corte con los ejes de cada una de las funciones, indicando el sentido físico de cada uno de estos puntos.
PUEDE INTERESAR LA CONSULTA DEL ARTÍCULO: MOVIMIENTO ARMÓNICO SIMPLE
b.1.- Hallar la velocidad máxima que alcanza el oscilador.
c.- Encontrar la ecuación/expresión de la función que nos indicaría la energía mecánica del oscilador armónico, E(x).
c.1.- Indicar el máximo valor de la energía cinética y el máximo valor de la energía potencial, comparándolo con el valor de la energía mecánica obtenido en el apartado anterior.
d.- Localizar el punto o puntos, indicando la posición y la energía correspondiente, en el que la energía cinética es igual que la potencial, obteniéndolos analíticamente.
e.- Obtener para la ecuación que responde a la energía cinética la posición de su punto crítico, confirmando analíticamente y a través de la primera y segunda derivada si es máximo o mínimo, así como la curvatura. Para este punto indicar además el sentido físico del mismo.
f.- Confirmar para la ecuación que responde a la energía potencial la posición de su punto crítico, confirmando analíticamente y a través de la primera y segunda derivada si es máximo o mínimo, así como la curvatura. Para este punto indicar además el sentido físico del mismo.
g.- Representar las tres funciones Ec(x), Ep(x) y E(x), con toda la información obtenida en los apartados anteriores.
h.- A través de geogebra, representar las tres funciones: Ec(x), Ep(x) y E(x), prestando atención al dominio de las funciones.
UTILIZACIÓN DE GEOGEBRA EN MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO.
i.- Indicar el valor de la constante k del oscilador armónico.
j.- Si la partícula que vibra tiene una masa de 25 g, indicar el valor del periodo de oscilación.
j.1.- Hallar el valor de la frecuencia angular (w).
k.- Teniendo en cuenta el valor de la masa del apartado anterior, obtener la ecuación de la posición, de la velocidad y de la aceleración en función del tiempo, sabiendo que en el instante inicial la partícula se encuentra en x=0 m. Representarlas en geogebra, intentando extraer conclusiones de las gráficas cinemáticas combinadas.
k.1.- Con la expresión de la velocidad, confirmar la velocidad máxima obtenida en el apartado b.1.
l.- Realizar el apartado anterior considerando que la partícula en el instante inicial se encuentra en la posición x=2 m.
PUEDE INTERESAR LA CONSULTA DEL ARTÍCULO: TRIGONOMETRÍA: ECUACIONES TRIGONOMÉTRICAS
m.- Realizar el apartado anterior considerando que la partícula en el instante inicial se encuentra en la posición x=-2 m.
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: RESOLUCIÓN PASO A PASO DEL EJERCICIO FQ1BE2549 DE MOVIMIENTO ARMÓNICO SIMPLE
OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS:
Posiblemente la aplicación operativa en matemáticas de mayor interés son los PROBLEMAS DE OPTIMIZACIÓN.
Por otro lado los ejercicios de CÁLCULO DE PARÁMETROS, suponen una consolidación del aprendizaje de ANÁLISIS DE FUNCIONES, donde podemos construir una función, estableciendo una serie de condiciones.
EJERCICIO M2BE2100. PROBLEMA DE OPTIMIZACIÓN:
Dividir un segmento de 6 cm de longitud en dos partes, con la propiedad de que la suma de las áreas del cuadrado y del triángulo equilátero construidos sobre ellos sea máxima.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/UZpwBucitbk
EJERCICIO M2BE1521, DE CÁLCULO DE PARÁMETROS:
Dada la función f(x) = ax2+ bx + c , determinar los valores de a , b y c para que se cumpla: que la gráfica de f(x) pase por el punto (0, 4) y que la recta y = – 4x + 7 sea tangente a la gráfica de f (x) en el punto de abscisa x = 1.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/13pDHPgLvtU
EJERCICIO M1BE2446:
Considerar la función f(x) = ax3 + bx2 + cx + d.
Hallar los coeficientes a, b, c y d sabiendo que f tiene un extremo relativo en el punto P (0,1) y que su gráfica tiene un punto de inflexión Q (-1,1).
EJERCICIO M1BE2447:
Sea f(x) = x4 + ax2 + bx + c. Obtener a, b y c para que en el punto de abscisa x=0, la recta tangente a la gráfica de f(x) sea y = 2x -1, y en el punto de abscisa x = 1 la recta tangente a la gráfica de f sea horizontal.
El extremo situado en el punto de abscisa x=1 ¿es máximo o mínimo?.
EJERCICIO M1BE2448:
Determinar una función de la forma f(x) = x3 + ax2 + bx + c , que tenga un extremo relativo en el punto de abscisa x=2 y para la cual el punto P (1,2) sea un punto de inflexión.
EJERCICIO M1BE2449:
Calcular el valor de los parámetros c y d sabiendo que la gráfica de la función definida por f(x) = 2x3 -x2 +cx +d, tiene como recta tangente en el punto P (1, -2) la recta de ecuación y = 5x – 7.
EJERCICIO M1BE2450:
Dada la función f(x) = x4 +ax3 + bx2 + cx + 7 :
Calcular los valores de a, b y c, sabiendo que se cumplen las condiciones siguientes:
- Dos de sus extremos relativos se encuentran en los puntos de abscisa x=0 y x=-2.
- La función corta el eje OX en el punto x=1.
Dar la expresión de la función resultante.
EJERCICIO M1BE2451:
Determinar los valores de a y b para que la función f(x) determinada por:
![]()
tenga un punto de inflexión en el punto (2, 8)
EJERCICIO M1BE2029:
Se sabe que la gráfica de la función siguiente f(x):
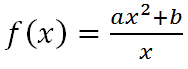
tiene una recta tangente horizontal en el punto P(2, 4). Hallar los valores de a y b.
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/KVSzz4y0xoQ
EJERCICIO M1BE2453:
Dada la función f(x) = ax2 + bx + c , determinar los valores de a, b y c para que se cumplan las siguientes condiciones:
- Que la gráfica de f(x) pase por el punto (0, 4).
- Que la recta y = -4x + 7 sea tangente a la gráfica de f(x) en el punto de abscisa x=1.
EJERCICIO M1BE2454:
Determinar una función f(x) = ax3 + bx2 + cs + d , sabiendo que su gráfica pasa por el punto P(-1,2) y tiene un punto de inflexión con tangente horizontal en Q(0, -2).
EJERCICIO M1BE2006:
Se desea construir un depósito con forma de prisma regular de base cuadrada. Además, el depósito es abierto (sin tapa superior). La capacidad total debe ser de 64 m3. El material de construcción de los laterales tiene un precio de 70 euros por m2, mientras que el de la base, más resistente, es de 140 euros por m2. Halle las dimensiones del depósito para que tenga el menor coste posible.
EJERCICIO M2BE2287:
Se desea vallar un terreno rectangular usando 100 m de una tela metálica. Se ha decidido dejar una abertura de 20 m sin vallar en uno de los lados de la parcela para colocar una puerta.
Calcular las dimensiones de todos los lados de la parcela rectangular de área máxima que puede vallarse de esa manera. Calcular el valor de dicha área máxima.
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE OPTIMIZACIÓN
EJERCICIO M1BE2007:
Halla a>0 y b>0 sabiendo que la gráfica de la función f: ℜ→ℜ, dada por:
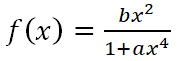
tiene en el punto (1, 2) un punto crítico.
EJERCICIO M1BE2008:
Se sabe que la gráfica de la función f definida por:

(para x≠1) tiene una asíntota oblicua que pasa por el punto (1, 1) y tiene pendiente 2. Calcula a y b.
EJERCICIO M1BE2014:
Hallar los coeficientes a, b y c sabiendo que la función definida por f(x)=x3+ax2+bx+c tiene en x=1 un punto de derivada nula que no es extremo relativo y que la gráfica de f pasa por el punto (1,1).
EJERCICIO M2BE309:
El dueño de un manantial de agua mineral llega a la siguiente conclusión: si el precio a que vende la botella es x euros, sus beneficios serán de –x2+10x-21 miles de euros al mes. Hallar:
a) ¿Qué precio debe poner para obtener un beneficio máximo?
b) ¿Cuál será ese beneficio?
c) ¿Entre que precios obtiene beneficios el agricultor?
d) Representar la función.
IR A LA RESOLUCIÓN DE ESTE EJERCICIO
EJERCICIO M2BE395:
Se desea cerrar con una cuerda dos parcelas rectangulares adyacentes (consecutivas) e iguales que encierran entre las dos un área de 1000 m2.
a) Encontrar la función que da la longitud de cuerda necesaria para cerrarlas.
b) ¿Cómo deben ser las parcelas para que el gasto de cuerda sea mínimo?
IR A LA RESOLUCIÓN DE ESTE EJERCICIO
EJERCICIO M1BE2470:
Se quiere vallar un campo rectangular que está junto a un camino. Si la valla del lado del camino cuesta 80 Euros/m y la de los otros 10 Euros/m. Hallar el área del mayor campo que puede cercarse con 28800 Euros.
EJERCICIO M1BE2471:
Se quiere construir un depósito abierto de base cuadrada y paredes verticales con capacidad para 13,5 metros cúbicos. Para ello se dispone de una chapa de acero de grosor uniforme. Calcular las dimensiones del depósito para que el gasto en chapa sea el menor posible.
EJERCICIO M1BE2472:
El propietario de un edificio tiene alquilados los 40 pisos del mismo a un precio de 600 € cada uno. Por cada 60€ que el propietario aumenta el precio observa que pierde un inquilino. ¿a qué precio le convienen alquilar los pisos para obtener la mayor ganancia posible?
EJERCICIO M1BE2473:
El consumo de un barco navegando a una velocidad de x nudos (millas/hora) viene dada por la expresión C(x)=(x2/60)+450/x. Calcular la velocidad más económica y el coste equivalente.
EJERCICIO M2BE2272 EBAU CANARIAS JUNIO 2023:
Se quiere construir una Casa de la Juventud de 240 m2 de superficie, que estará rodeada por una zona ajardinada con las dimensiones de la imagen.
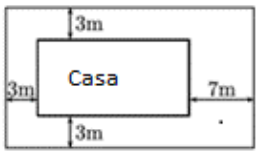
Si se quiere minimizar la superficie total de la zona ajardinada, ¿qué dimensiones debe tener la Casa de la Juventud? ¿Cuál es el área de la zona ajardinada?.
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE PROBLEMA DE OPTIMIZACIÓN: MATEMÁTICAS II. E.B.AU. CANARIAS 2023. EJERCICIOS RESUELTOS. CONVOCATORIA ORDINARIA JUNIO
EJERCICIOS M1BE2013:
IR A RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN CON SOLUCIÓN
MÁS MATERIALES DE OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS, COMO APLICACIÓN DE LA DERIVADA EN: APLICACIONES DE LA DERIVADA. OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS.
OPTIMIZACIÓN:
PROBLEMAS DE OPTIMIZACIÓNCÁLCULO DE PARÁMETROS:
132 APLICACIONES DE LA DERIVADA. CALC PARAMETROS V3EJERCICIO M2BE2017:
Dada la función:
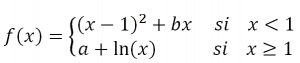
a.- Estudia los valores de los parámetros a y b para que la función f(x) sea continua y derivable en ℜ. Escribe la función resultante f(x).
b.- Tomando los valores a=-2 y b=1, calcula la ecuación de la recta tangente en x=e.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/foUIAm2GnC4
INTERESA IR A EJERCICIOS DE ESTUDIO DE LA DERIVABILIDAD DE UNA FUNCIÓN
RECTA TANGENTE Y RECTA NORMAL A UNA CURVA:
EJERCICIO M2BE2333:
Obtener la ecuación de la recta tangente y la recta normal a la curva f(x) = Ln ((x+1)/(x-1)), en el punto de abscisa x=3
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/GRbly7emcLk
SE PROPONE LA CONSULTA DE LOS SIGUIENTES MATERIALES:
- REPRESENTACIÓN DE FUNCIONES ESPECIALES. «LAS PARDELAS»
- PROPUESTA DE EVALUACIÓN FUNCIONES 1º BACHILLERATO
- REPASO ANÁLISIS MATEMÁTICAS 1º BACHILLERATO
INTEGRALES Y APLICACIONES EN EL CÁLCULO DE ÁREAS:
CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
REGLAS BÁSICAS PARA LA RESOLUCIÓN DE INTEGRALES:
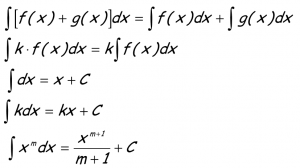
OBTENCIÓN DE LA INTEGRAL DEFINIDA SEGÚN LA REGLA DE BARROW:
Siendo F(x) una primitiva de f(x), esto es: F(x) es el resultado de la integral indefinida de f(x)
La forma de trabajar habitual es la siguiente: Se resuelve la integral como si fuera indefinida (se obtiene la primitiva F(x)) y se introduce entre corchetes, indicando los límites de integración superior e inferior; en el siguiente paso se sustituye la x de la expresión de la integral resuelta (primitiva) primero por el límite superior F(b) y se le resta la expresión sustituida la x por el límite inferior F(a), tal como indica la regla de Barrow. Hay que tener cuidado con los signos, ya que se producen muchos errores.
EJEMPLO:
CÁLCULO DE ÁREAS ENCERRADAS POR UNA FUNCIÓN Y EL EJE OX, UTILIZANDO LA INTEGRAL DEFINIDA:
El cálculo de áreas encerradas por la función y el eje de abscisas presenta un problema a nivel práctico y es que si la función es negativa, se encuentra por debajo del eje de las x, la integral también lo es. Por ello, desde el punto de vista práctico lo que se hace es lo siguiente, según estos tres casos:.
A) SI LA FUNCIÓN ES TODA POSITIVA, DESDE a HASTA b: (Se encuentra por encima del eje OX), el resultado de la integral definida es igualmente positivo y coincide con el área del recinto determinado por la función, el eje X y las rectas x=a y x=b.
B) SI LA FUNCIÓN ES TODA NEGATIVA, DESDE a HASTA b: (Se encuentra por debajo del eje OX), el resultado de la integral definida es negativo, pero en valor absoluto coincide con el área del recinto, por lo que:
C) Si la función desde a hasta b, toma valores POSITIVOS Y NEGATIVOS, generando recintos de áreas por encima y debajo del eje OX, en subintervalos (corta al eje de las x en uno o varios puntos), el resultado de la integral definida de a hasta b, compensa las áreas positivas con las negativas, dando un resultado que no es el que se nos pide. Lo que se hace en estos casos es localizar los puntos de corte de la función con el eje X que se encuentran entre a y b, y ordenarlos de mayor a menor empezando en a y terminando en b, entonces, el área:
Se subdivide en integralitas más pequeñas, utilizando los valores absolutos para que las áreas positivas no compensen las negativas y el resultado realmente coincida con el área
CÁLCULO DE ÁREAS ENCERRADAS POR DOS FUNCIONES, UTILIZANDO LA INTEGRAL DEFINIDA:
En General el área encerrada por dos funciones f(x) y g(x):
Es decir «la integral definida entre los puntos de corte entre las dos funciones, de la resta de las dos funciones que generan el recinto».
En este ejemplo que se muestra, la función f(x), parábola abierta hacia abajo (la función que está por encima) corresponde a:
f(x)= -x2 – 5x + 3
Y la función que se encuentra por debajo, g(x), parábola abierta hacia arriba corresponde a:
g(x) = x2 + 3x + 1
Si la primera de las funciones de la integral (la que equivale al minuendo de la resta) es la que está por encima, el resultado de la integral es positivo, correspondiendo al valor del área.
Si por el contrario lo hacemos al revés, el resultado de la integral es negativa. El área entonces corresponde al resultado de la integral cambiado de signo.
Por ello debemos tener en cuenta:
- a y b son los puntos de corte de las dos funciones, que se pueden calcular resolviendo el sistema formado por las dos funciones, normalmente por igualación de ellas.
- Si el resultado da negativo es porque la función f(x) no es la que está por encima de g(x).
Si las funciones se cortan en varios puntos, no se puede hacer la integral en un solo golpe, sino a trozos, definidos por los sucesivos cortes de las funciones entre sí, para que resultados de áreas positivas no compensen a las negativas.
El siguiente ejemplo corresponde concretamente a estas dos funciones:
f(x) = 3x3 + 2x2 – 3x + 1
g(x) = 2x3 – 2x2 + 5x + 1
En este caso, debemos tener en cuenta que la función que inicialmente está por encima, en el siguiente recinto se encuentra por debajo, con lo cual lo mejor es recurrir a los valores absolutos, de las integrales subdivididas con los puntos de corte ordenados. Por ello:
o con los valores absolutos y despreocupándonos de qué función se encuentra por encima en cada tramo:
EJERCICIOS M2BP187:
1. Calcula el área del recinto limitado por la parábola y = x2 , y las rectas: y = 0, x = 2 , x = 6.
2. Calcula el área del recinto limitado por la parábola de ecuación y = 9 – x2 y el eje de abscisas.
3. Calcula el área del recinto limitado por la parábola y = 4x – x2 y el eje de abscisas en el intervalo [0,6].
4. Halla el área comprendida entre las parábolas f(x) = 8 – x2 , g(x) = x2
5. Halla el área del recinto limitado por la parábola de ecuación y = x2 , la recta de ecuación y = x+2 y el eje OX.
EJERCICIO M1BE2455:
Hallar el área encerrada por las función y = -x2 + 3 y el eje OX
EJERCICIO M1BE2456:
Hallar el área encerrada por las funciones f(x) = x , x=3 y el eje OX
EJERCICIO M1BE2457:
Hallar el área encerrada por y = x3 – x y el eje OX.
EJERCICIO M1BE2458:
Calcular el área comprendida entre la gráfica de la función y = x3 – 6x2 + 8x y el eje OX, haciendo un dibujo aproximado y explicando.
EJERCICIO M2BE2422:
Dibuja y calcula el área encerrada entre la función f(x) = x2 – 4x y g(x) = 3 – 2x.
IR AL ARTÍCULO QUE CONTIENE LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE CÁLCULO DE ÁREAS CON LA INTEGRAL DEFINIDA: EXAMEN DE ANÁLISIS DE FUNCIONES, ÁLGEBRA, GEOMETRÍA ESPACIAL Y PROBABILIDAD PARA MATEMÁTICAS II DE 2º BACHILLERATO
EJERCICIO M1BE2475:
Representar la región delimitada por las funciones, f(x) = x2 + x +1 y g(x) = 1 – x.
Hallar el área de la región.
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.
EJERCICIO M1BE2459:
Dada la parábola de ecuación y = 4 – x2 y la recta de ecuación y = x + 2
a.- Hallar los puntos de intersección entre las funciones anteriores.
b.- Esbozar el gráfico señalando el recinto limitado por ambas funciones.
c.- Calcular el área del recinto limitado por las dos funciones.
EJERCICIO M1BE2460:
Dibujar el recinto limitado por las funciones f(x) = 2x2 – 4x +3 y g(x) = x2 – 2x + 3 y calcular el área de este recinto.
EJERCICIO M1BE2461:
Hallar el área encerrada por el eje OX, la función f(x) = |x| , las rectas x=-2 y x=2. Dibujar el recinto correspondiente e intentar un contraste con estrategias geométricas básicas anteriores.
EJERCICIO M1BE2462:
Hallar el área encerrada por el eje OX, la función f(x) = |x – 1| , las rectas x=-2 y x=1. Dibujar el recinto correspondiente e intentar un contraste con estrategias geométricas básicas anteriores.

Comments are closed, but trackbacks and pingbacks are open.