MOVIMIENTO ARMÓNICO SIMPLE FÍSICA
Cuando yo estiro (o comprimo) un resorte, la reacción del muelle es una fuerza elástica, de sentido contrario a la fuerza que yo hago, descrita por la ley de Hooke.
Si soltamos el cuerpo, a causa de esta fuerza elástica, el objeto describirá un movimiento de vaivén (decimos que vibra –vibratorio-) en torno a la posición de equilibrio. Suponiendo que no exista rozamiento el movimiento será infinito y siempre con la misma amplitud.
Se obtiene un movimiento de vibratorio, que aparece con frecuencia en la naturaleza y que se denomina MOVIMIENTO ARMONICO SIMPLE (MAS).
La forma de proceder para obtener las ecuaciones características del movimiento será relacionarlo con el movimiento circular uniforme y considerar las proyecciones de este movimiento sobre los ejes habituales horizontal y vertical.
Este movimiento es introductorio para el MOVIMIENTO ONDULATORIO.
ASPECTOS FORMALES PARA DOCENTES, ACTUALIZADOS A LA LOMLOE, AL FINAL DEL ARTÍCULO, PARA NO INTERFERIR CON LO QUE ES DE INTERÉS PARA EL APRENDIZAJE CON LOS ALUMNOS.
MATERIAL AUDIOVISUAL DE MOVIMIENTO ARMÓNICO SIMPLE, PREVIO A LA REALIZACIÓN DE LOS EJERCICIOS PROPUESTOS:
EXPLICACIÓN TEÓRICA DEL MOVIMIENTO ARMÓNICO SIMPLE, MATERIAL AUDIOVISUAL EN FORMATO CLASE Y OBTENCIÓN DE LA ECUACIÓN DEL MOVIMIENTO CARACTERÍSTICO, RELACIONÁNDOLO CON EL MOVIMIENTO CIRCULAR UNIFORME, LO CUAL NOS PROPORCIONA LA POSIBILIDAD DE PONERLO EN FUNCIÓN DE PARÁMETROS INTERESANTES COMO EL PERIODO Y LA FRECUENCIA ANGULAR:
UNA VEZ HEMOS OBTENIDO LA ECUACIÓN DE LA POSICIÓN, DERIVÁNDOLA PODREMOS OBTENER LA EXPRESIÓN DE LA VELOCIDAD Y DE LA ACELERACIÓN DEL MOVIMIENTO ARMÓNICO SIMPLE. OBTENDREMOS POR LO TANTO LAS ECUACIONES CINEMÁTICAS DEL M.A.S.:
EL MOVIMIENTO ARMÓNICO SIMPLE DE UN OSCILADOR ARMÓNICO ES LA CONVERSIÓN DE ENERGÍAS POTENCIALES ELÁSTICAS EN ENERGÍAS CINÉTICAS, AL IGUAL QUE OCURRE EN UN PÉNDULO SIMPLE. SE AÑADE LA GRÁFICA DE ENERGÍAS CORRESPONDIENTE Y EN COMPARATIVA:
CON LAS CARACTERÍSTICAS DINÁMICAS DEL MOVIMIENTO ARMÓNICO SIMPLE (UTILIZANDO LA SEGUNDA LEY DE NEWTON PARA ESTE MOVIMIENTO INTERESANTE) Y RELACIONÁNDOLO CON EL MOVIMIENTO DE VAIVEN DE UN PÉNDULO SIMPLE, PODEMOS MEDIR LA ACELERACIÓN DE LA GRAVEDAD EN CUALQUIER SITIO, INCLUSO EN CLASE, QUE LO HAREMOS:
EJERCICIO F2BE0118:
Un muelle elástico de 10 cm tiene uno de sus extremos fijo en una pared vertical y descansa en una superficie horizontal sin rozamiento.
Se le aplica una fuerza de 20 N para mantenerlo estirado una longitud de 5 cm.
En esta posición se suelta y oscila libremente con un período de oscilación de 4 segundos. Calcular:
- La constante de recuperación del resorte.
- La ecuación del movimiento vibratorio armónico resultante.
- Las energías potencial y cinética cuando x=2 cm.
- La velocidad y aceleración máximas, indicando las elongaciones que corresponden a cada una de ellas.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/1td7hMbs1xo
IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA TRUEQUE (EXAMEN DE MEJORA) DE FÍSICA PARA FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO
EJERCICIO FQ1BE2222:
De un movimiento armónico simple que tiene una frecuencia de 2 Hz, sabemos que en el instante inicial su elongación es máxima y positiva; y que en ese mismo instante su aceleración en valor absoluto es de 4π2 m/s2.
Hallar la ecuación del movimiento en función del tiempo.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/a8jZeS61PDc
EJERCICIO FQ1BE2253m (X821):
Una bolita de corcho sobre el agua de la Charca de Maspalomas, oscila con un m.a.s., con un período de 3 segundos, entre dos puntos separados 10 cm, subiendo y bajando en la vertical. Si se considera que en el instante inicial, la elongación es la más alta de sus posiciones, determinar:
- La ecuación del movimiento de la bolita en función del coseno.
- La ecuación del movimiento de la bolita en función del seno.
- La velocidad y la aceleración en función del tiempo, partiendo de la ecuación obtenida en el apartado a.
- Los valores máximos de la velocidad y la aceleración, y las posiciones donde se alcanzan dichos valores.
SOLUC.: 1.- y(t)=0,05·cos(2π/3 t)…
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/wF16-DmgBxM
EJERCICIO FQ1BE2223:
De un movimiento armónico simple que tiene una frecuencia de 1 Hz, sabemos que en el instante inicial su elongación es máxima y negativa; y que en ese mismo instante su aceleración es π2/100 m/s2.
Hallar la ecuación del movimiento. Utilizar la expresión en función del seno y en función del coseno.
EJERCICIO FQ1BE2225:
En el dibujo se representa la elongación en función del tiempo, de un movimiento armónico simple determinado.
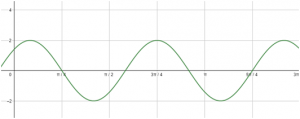
a.- Indicar la amplitud.
b.- Indicar el periodo
c.- Hallar la fase inicial, teniendo en cuenta que la elongación en el instante inicial es positiva, según se observa.
d.- Poner la ecuación del movimiento. Confirmar con geogebra.
e.- Obtener el primer instante en el que se alcanza la máxima elongación.
f.- Indicar el valor de la velocidad y de la aceleración en el instante del apartado anterior.
IR A LA SOLUCIÓN (SÓLO PARA DOCENTES)
Los alumnos pueden comprobar que es correcta su ecuación, representándola en geogebra.
EJERCICIO FQ1BE2226:
En el dibujo se representa la elongación en función del tiempo, de un movimiento armónico simple determinado.
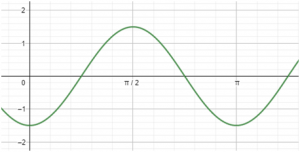
a.- Indicar la amplitud.
b.- Indicar el periodo
c.- Hallar la fase inicial, teniendo en cuenta que la elongación en el instante inicial es negativa según se observa.
d.- Poner la ecuación del movimiento. Confirmar con geogebra.
e.- Obtener el primer instante en el que se alcanza la máxima elongación.
f.- Indicar el valor de la velocidad y de la aceleración en el instante del apartado anterior.
IR A LA SOLUCIÓN (SÓLO PARA DOCENTES)
Los alumnos pueden comprobar que es correcta su ecuación, representándola en geogebra.
EJERCICIO FQ1BE2227:
Para la función f(x)=a·sen(bx+πc), que responde a un movimiento armónico simple, hallar a,b y c sabiendo que la función corta al eje OX en el punto -π/20, en el intervalo (-π,0); que pasa por el punto (π/4, -1/2), en el intervalo (0,2π) , siendo este último punto además un extremo relativo para la función.
IR A LA SOLUCIÓN (SÓLO PARA DOCENTES)
Los alumnos pueden comprobar que es correcta su ecuación, representándola en geogebra.
EJERCICIO FQ1BE2254:
La siguiente representación de la elongación vertical (m) frente al tiempo (s) de un M.A.S. responde al movimiento de un surfero de 70 kg en Playa del Hombre, en Telde de Gran Canaria, en un momento en que sencillamente se deja llevar por la onda a la que está sometido, sin decidirse a tomar la ola.
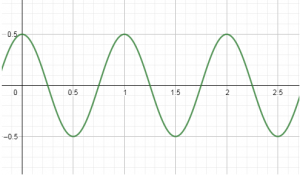
Al respecto se pide:
a.- La ecuación del movimiento armónico, en función del seno.
b.- La ecuación del movimiento, en función del coseno.
c.- El valor de la Energía potencial máxima y un instante del intervalo (0,1) donde se alcance.
d.- La elongación en la que el surfero tiene una energía cinética igual que la potencial. Si son varias, indicarlo.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/3Rb9tGg5FlQ
EJERCICIO FQ1BE2249 (X822):
En la gráfica que se muestra se representa la elongación (en metros) frente al tiempo (en segundos), según se indica, del movimiento armónico de un surferillo miedoso de 65 kg, en la Cícer, en Las Canteras (la mejor playa urbana del mundo).
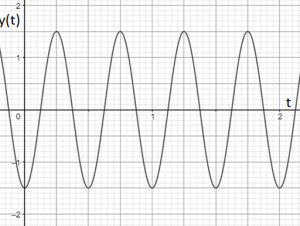
a.- Indicar el valor de la amplitud del movimiento y del periodo.
b.- Obtener la ecuación del movimiento.
c.- Indicar el valor de la frecuencia angular, de la frecuencia y de la fase inicial.
d.- Indicar un instante de tiempo correspondiente al intervalo (0,1), en el que la energía potencial sea máxima.
e.- Indicar un instante de tiempo dentro del mismo intervalo (0,1) , en el que la energía cinética sea máxima.
f.- Hallar el valor de la energía mecánica de este movimiento, comentando el modo en que varía esta energía a lo largo del tiempo.
SOL: A=1,5 m; T=0,5 s; y=1,5·sen(4πt+3π/2); w=4π rad/s; f=2 Hz; φo=3π/2 rad; 0,5 s; 0,375 s; 11547,44 J (no varía)
EJERCICIO FQ1BE2250 (X822):
Comprimiendo un resorte horizontal y soltándolo, conseguimos que un cuerpo unido a él, oscile armónicamente en la horizontal, entre dos posiciones extremas separadas 25 cm, con una frecuencia de 5 Hz.
Hallar la ecuación del movimiento, considerando el instante inicial el momento en el que lo soltamos.
SOLUC.: x(t)=0,125·sen(10πt+3π/2)
EJERCICIO FQ1BE2251 (X822):
Un cuerpo de 10 kg de masa se sabe que describe un movimiento armónico simple que tiene una frecuencia angular de π rad/s, sabemos que en el instante inicial se encuentra en la posición de equilibrio; y que en ese mismo instante su velocidad es + 0,1π m/s. (3 puntos)
a.- Indicar la ecuación del movimiento en función del coseno.
b.- Hallar la posición en la que la energía cinética del cuerpo es igual a su energía potencial.
SOLUC.: x(t)=0,1·cos(πt+3π/2); 0,071 m
EJERCICIO FQ1BE2252 (X821):
Disponemos de un cuerpo de 200 g de masa, situado en una superficie horizontal sin rozamiento, unido a un resorte sujeto a una pared vertical, de constante elástica 80 N/m.
En cierto instante, separamos el cuerpo de su posición de equilibrio, comprimiendo el resorte 2,5 cm y al soltarlo comienza a oscilar libremente.
a.- Obtener la ecuación del movimiento armónico que se produce, considerando el instante inicial el momento en el que soltamos el cuerpo.
b.- Especificar el valor de la amplitud, el periodo, la frecuencia, la frecuencia angular y la fase inicial. (0,75 p.)
c.- Plantear la otra ecuación del movimiento, la que no se ha planteado en el apartado a. Seno o coseno según corresponda.
d.- Obtener las ecuaciones de la velocidad y la aceleración, partiendo de la ecuación de la elongación en función del seno.
e.- Indicar la velocidad máxima del movimiento, así como el valor de la elongación donde se produce. (0,75 p.)
f.- Indicar la aceleración máxima del movimiento, así como el valor de la elongación donde se produce. (0,75 p.)
g.- Hallar las energías cinética y potencial en el instante inicial.
h.- Hallar las energías cinética y potencial en la posición de equilibrio.
i.- Hallar la posición en la que la Energía cinética es la cuarta parte que la potencial.
SOLUC.: x(t)=0,025·sen(20t+3π/2); A=0,025 m; T=π/10 s; f=10/π Hz; w=20 rad/s; φo=3π/2 rad; x(t)=0,025·cos(20t+π); …; ±0,5 m/s; ±0,125 m/s2; …; …; ±0,022 m
EJERCICIO F4EE2114: Ejercicio curioso de interés para valorar el uso correcto de las estrategias matemáticas involucradas.
Un resorte alcanza una longitud de 34 cm cuando se le aplica una fuerza de 250 N; si se le aplica una fuerza de 170 N alcanza una longitud de 25 cm. Hallar:
a.- La longitud del resorte sin deformar.
b.- La constante elástica del resorte.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/-8a1h0gf1BE
EJERCICIO FQ1BE2592:
En la siguiente gráfica se representa la elongación (m), frente al tiempo de Miguel (s), un surferillo miedoso, que realiza un M.A.S., mientras espera la ola de sus sueños en la Cicer en Las Palmas de G.C.
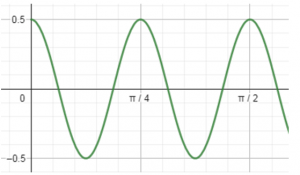
A.- Hallar la amplitud, la frecuencia angular (rad/s), la frecuencia (Hz) y el periodo del movimiento.
B.- Obtener la ecuación del movimiento en función del seno.
C.- Con la expresión anterior, obtener la ecuación de la velocidad en función del tiempo y de la aceleración en función del tiempo.
D.- Obtener la ecuación del movimiento en función del coseno.
E.- Indicar un punto en el intervalo (0, π/2) en el que la energía potencial sea máxima.
F.- Indicar un punto en el intervalo (0, π/2) en el que la energía cinética sea máxima.
G.- Si la masa de Miguel es de 71 kg, hallar el valor de la energía mecánica e indicar razonadamente el modo en que la energía mecánica varía a lo largo del tiempo.
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE MOVIMIENTO ARMÓNICO SIMPLE: PRUEBA DE EXAMEN DE FÍSICA Y QUÍMICA 1º BACHILLERATO. MOVIMIENTOS PARABÓLICO Y ARMÓNICO SIMPLE
EJERCICIO FQ1BE2549, TAREA INTERDEPARTAMENTAL MAT/FYQ:
Sabemos que en un oscilador armónico, cuerpo que se mueve con un movimiento armónico simple, en ausencia de rozamientos, se conserva la energía mecánica, que es igual a la suma de la energía cinética y la energía potencial:
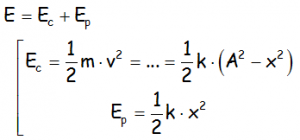
Para un movimiento armónico, cuyas expresiones de la energía cinética y la potencial en función de la posición responde a: Ec(x) = 10 – 2,5 x2 ; Ep(x) = 2,5 x2 . Para una partícula de 25 g de masa que vibra según se indica, responder a las siguientes cuestiones:
a.- Identificar la amplitud del movimiento.
b.- Localizar analíticamente los puntos de corte con los ejes de cada una de las funciones, indicando el sentido físico de cada uno de estos puntos.
b.1.- Hallar la velocidad máxima que alcanza el oscilador.
c.- Encontrar la ecuación/expresión de la función que nos indicaría la energía mecánica del oscilador armónico, E(x).
c.1.- Indicar el máximo valor de la energía cinética y el máximo valor de la energía potencial, comparándolo con el valor de la energía mecánica obtenido en el apartado anterior.
d.- Localizar el punto o puntos, indicando la posición y la energía correspondiente, en el que la energía cinética es igual que la potencial, obteniéndolos analíticamente.
e.- Obtener para la ecuación que responde a la energía cinética la posición de su punto crítico, confirmando analíticamente y a través de la primera y segunda derivada si es máximo o mínimo, así como la curvatura. Para este punto indicar además el sentido físico del mismo.
f.- Confirmar para la ecuación que responde a la energía potencial la posición de su punto crítico, confirmando analíticamente y a través de la primera y segunda derivada si es máximo o mínimo, así como la curvatura. Para este punto indicar además el sentido físico del mismo.
g.- Representar las tres funciones Ec(x), Ep(x) y E(x), con toda la información obtenida en los apartados anteriores.
h.- A través de geogebra, representar las tres funciones: Ec(x), Ep(x) y E(x), prestando atención al dominio de las funciones.
UTILIZACIÓN DE GEOGEBRA EN MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO.
i.- Indicar el valor de la constante k del oscilador armónico.
j.- Si la partícula que vibra tiene una masa de 25 g, indicar el valor del periodo de oscilación.
j.1.- Hallar el valor de la frecuencia angular (w).
k.- Teniendo en cuenta el valor de la masa del apartado anterior, obtener la ecuación de la posición, de la velocidad y de la aceleración en función del tiempo, sabiendo que en el instante inicial la partícula se encuentra en x=0 m. Representarlas en geogebra, intentando extraer conclusiones de las gráficas cinemáticas combinadas.
k.1.- Con la expresión de la velocidad, confirmar la velocidad máxima obtenida en el apartado b.1.
l.- Realizar el apartado anterior considerando que la partícula en el instante inicial se encuentra en la posición x=2 m.
PUEDE INTERESAR LA CONSULTA DEL ARTÍCULO: TRIGONOMETRÍA: ECUACIONES TRIGONOMÉTRICAS
m.- Realizar el apartado anterior considerando que la partícula en el instante inicial se encuentra en la posición x=-2 m.
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: RESOLUCIÓN PASO A PASO DEL EJERCICIO FQ1BE2549 DE MOVIMIENTO ARMÓNICO SIMPLE
IR A OTROS RECUERSOS Y EJERCICIOS DE MOVIMIENTO ARMÓNICO SIMPLE: https://matematicasfisicaquimica.com/ejercicios-resueltos-movimiento-armonico-simple-fisica-bachillerato/
Documento con apuntes y ejercicios relacionados con este material audiovisual:
131 MOVIMIENTO ARMONICO SIMPLE V6ASPECTOS FORMALES PARA DOCENTES ACTUALIZADOS LOMLOE:
SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS:
- COMPETENCIA MATEMÁTICA Y EN CIENCIA, TECNOLOGÍA E INGENIERÍA (STEM), concretamente el DESCRIPTOR OPERATIVO STEM1.
- COMPETENCIA EN COMUNICACIÓN LINGÜÍSTICA (CLL), concretamente el DESCRIPTOR OPERATIVO CCL2.
- COMPETENCIA DIGITAL (CD), concretamente el DESCRIPTOR OPERATIVO CD1.
- COMPETENCIA PERSONAL, SOCIAL Y DE APRENDER A APRENDER (CPSAA), concretamente el DESCRIPTOR OPERATIVO CPSAA1.1
- COMPETENCIA EMPRENDEDORA (CE), concretamente el DESCRIPTOR OPERATIVO CE1
CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS I DE 1º DE BACHILLERATO
MATI1BAC1.1 , MATI1BAC1.2 , MATI1BAC2.1 , MATI1BAC2.2 , MATI1BAC3.1 , MATI1BAC4.1 , MATI1BAC5.1 , MATI1BAC5.2 , MATI1BAC6.1 , MATI1BAC6.2 , MATI1BAC7.1 , MATI1BAC7.2 , MATI1BAC8.1 , MATI1BAC8.2 , MATI1BAC9.1 , MATI1BAC9.2 , MATI1BAC9.3
SE OBSERVAN LAS COMPETENCIAS ESPECÍFICAS DE MATEMÁTICAS I Y II Y ESTÁN HIPERVINCULADOS A LOS DESCRIPTORES OPERATIVOS DE LAS COMPETENCIAS CLAVE
GUARDA RELACIÓN CON ASPECTOS DEL PERFIL DE SALIDA DEL ALUMNADO
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS:



Comments are closed, but trackbacks and pingbacks are open.