ÓPTICA GEOMÉTRICA DEFECTOS OJO

ÓPTICA GEOMÉTRICA Y LUZ. DEFECTOS DEL OJO:

La ÓPTICA GEOMÉTRICA se ocupa de los fenómenos ópticos que pueden ser interpretados considerando únicamente que la luz está constituida por rayos rectilíneos que proceden de un foco emisor. Con esta idea se pueden explicar los fundamentos de los dispositivos ópticos como espejos, lentes y aparatos más complicados como microscopios y telescopios.

ECUACIÓN FUNDAMENTAL DEL DIOPTRIO ESFÉRICO. Punto de partida del resto de las ecuaciones que se obtendrán: dioptrio plano, espejo plano, espejo esférico y lentes.
CONVENIO DE SIGNOS EN ÓPTICA GEOMÉTRICA
ECUACIÓN DEL DIOPTRIO PLANO
- EJERCICIOS RESUELTOS DE APLICACIÓN DEL DIOPTRIO PLANO. ÓPTICA GEOMÉTRICA PARA FÍSICA DE BACHILLERATO
FOCO OBJETO Y FOCO IMAGEN, FORMACIÓN DE IMÁGENES EN EL DIOPTRIO ESFÉRICO
AUMENTO LATERAL EN EL DIOPTRIO ESFÉRICO, ESPEJOS ESFÉRICOS Y LENTES
- OBTENCIÓN DE LA ECUACIÓN DE HEMHOLTZ PARA EL DIOPTRIO ESFÉRICO
- AUMENTO LATERAL A TRAVÉS DE LA ECUACIÓN DE HEMHOLTZ
AUMENTO ANGULAR EN EL DIOPTRIO ESFÉRICO, RELACIÓN CON AUMENTO LATERAL
ECUACIÓN DEL ESPEJO ESFÉRICO, FOCOS EN EL ESPEJO ESFÉRICO
ECUACIÓN DEL ESPEJO PLANO
LENTES. ECUACIÓN FUNDAMENTAL DE LAS LENTES DELGADAS
FOCOS Y DISTANCIAS FOCALES EN LAS LENTES. POTENCIA DE UNA LENTE. CONSTRUCCIÓN DE IMÁGENES EN LAS LENTES
TIPOS DE LENTES habituales en ejercicios de óptica geométrica para Física de Bachillerato.
Ejercicios de óptica geométrica, con las soluciones: EJERCICIOS ÓPTICA
VISIÓN DEL COLOR
DISPERSIÓN DE LA LUZ EN EL PRISMA ÓPTICO
ESPECTROSCOPÍA ÓPTICA
INTRUMENTOS ÓPTICOS. ÓPTICA GEOMÉTRICA

LEY DE SNELL DE LA REFRACCIÓN Y REFLEXIÓN, PARA ÓPTICA Y ONDAS:

$refracción de frente de onda$

En el dibujo, la onda viaja por el medio 1 y al llegar a la superficie de separación de los dos medios comienza a moverse por el medio 2. En el caso planteado en la figura, la velocidad de la onda en el medio 2 es menor que en el medio 1; notar que es como si a la onda le costara más ir desde B a B’ que de A a A’.

Como [espacio=velocidad·tiempo];

El punto B recorre en el medio 2 la distancia BB’=v₂t,

El punto A recorre en el medio 1 la distancia AA’=v₁t.

Dividiendo se obtiene:

Además:

Dividiendo los dos senos:

Ya que el índice de refracción de un medio determinado se define como la velocidad de la luz (o del fenómeno ondulatorio) en el vacío entre la velocidad de la luz (o del fenómeno ondulatorio) en el medio considerado:

$indice de refracción$

Con lo que la Ley de Snell queda:

$ley de snell de la refracción$

Donde n₁ y n₂ son los índices de refracción de cada uno de los medios. Los ángulos φ₁ y φ₂ son los ángulos de incidencia y refracción respectivamente.

La Ley de Snell indica las LEYES DE LA REFRACCIÓN:

1. Una onda que incide oblicuamente sobre una superficie plana que separa dos medios se refracta, y la razón de los senos de los ángulos de incidencia y de refracción es igual al cociente de las velocidades del primer medio y del segundo. Dicho cociente también mide el índice de refracción.

2. Los ángulos de incidencia y de refracción son coplanarios.

En el caso de la REFLEXIÓN:

El ángulo de incidencia y el de reflexión son el mismo, no hay más que ver que al pasar una onda de un medio al mismo, los índices de reflexión son iguales y en consecuencia los ángulos:

ÁNGULO LÍMITE Y REFLEXIÓN TOTAL:

Se define el ángulo límite como el ángulo de incidencia a partir del cual se produce sólo reflexión (reflexión total). Para valores superiores a ese ángulo límite los rayos se reflejan, no se refractan, no cambian de medio, se quedan en el que está. Este fenómeno de la reflexión total es lo que determina la utilidad de la fibra óptica como medio de transporte de información a través de pulsos de luz.

También se define como el mayor ángulo de incidencia que produce refracción. A partir de ese ángulo de incidencia se produce entonces REFLEXIÓN TOTAL.

De lo anterior se deduce que es el comportamiento que sigue, o debe seguir la luz dentro de la fibra óptica, de tal manera que la luz se quede dentro de la tubería que es la fibra, a través de sucesivas reflexiones en las paredes de la misma.

Si tenemos en cuenta la Ley de Snell de la Refracción:

n₁· sen i = n₂· sen r ; donde i es el ángulo de incidencia y r el ángulo de refracción

estamos buscando el ángulo límite (i) que llamaremos L, para el cual el ángulo de refracción es de 90º,

n₁· sen L = n₂· sen 90 ; como el seno de 90º es igual a 1,

nos queda que: sen L = n₂/n₁ con lo que teniendo en cuenta que el seno de un ángulo es menor que 1 (o igual a uno) tendrá que ocurrir que el índice de refracción del segundo medio tiene que ser menor que el del primero. Con lo cual sólo se produce reflexión total de la luz si la luz pasa de un medio a otro menos refringente, con menor índice de refracción que el primero.

ÍNDICE DE REFRACCIÓN (n) de un medio cualquiera es el cociente entre la velocidad de la luz en el vacío y la velocidad de la luz en un medio cualquiera: n=c/v

Como la luz donde lleva mayor velocidad es en el vacío, el índice de refracción siempre es mayor o igual a uno. No tiene unidades, evidentemente.

EJEMPLOS DE ÍNDICES DE REFRACCIÓN USUALES EN ÓPTICA:

n_vacío = 1 ; n_aire = 1,0003 ≅ 1 ; n_agua = 1,33 ; n_vidrio ≅ 1,6

Por ello, se producirá reflexión total cuando el rayo pasa de vidrio a aire (caso de la fibra óptica), de vidrio a agua o de agua a aire, en suma a otro medio con un índice de refracción inferior al del primer medio.

En la fibra óptica, gracias a este fenómeno la luz puede viajar por su interior casi sin pérdidas, aunque se doble la fibra.

EJERCICIO F2BE1292:

Calcula el índice de refracción de una sustancia respecto del aire sabiendo que su ángulo límite es de 30º.

DATO: n_aire=1

Vídeo donde se resuelve este ejercicio y se añaden breves explicaciones teóricas: https://youtu.be/N6Ia2kTJPVc

EJERCICIO F2BE1293:

Un rayo de luz monocromática que se propaga en un medio de índice d refracción 1,58 penetra en otro medio de índice de refracción 1,23 formando un ángulo de incidencia de 15º (respecto a la normal) en la superficie de discontinuidad entre ambos medios.

a.- Determinar el valor de ángulo de refracción correspondiente al ángulo de incidencia anterior.

b.- Definir ángulo límite y calcular el valor para los dos medios anteriores.

Enlace al vídeo donde se resuelve este ejercicio: https://youtu.be/p2cPi_guzAg

EJERCICIO F2BE2427:

Un rayo de luz que se propaga en un cristal de cuarzo tiene un ángulo límite de 39^o respecto del vacío. Hallar la velocidad de la luz en el cristal de cuarzo.

DATO: v_{luz en el vacío}=3·10⁸ m/s

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: PRUEBA DE EXAMEN DE FÍSICA DE 2º DE BACHILLERATO

EN EL VACÍO, LAS ONDAS ELECTROMAGNÉTICAS (ONDAS DE RADIO, LUZ…) VIAJAN A LA VELOCIDAD DE LA LUZ. CUANDO SE PROPAGAN EN UN MEDIO MATERIAL, SE FRENAN DEPENDIENDO DE LAS CARACTERÍSTICAS DEL MEDIO. EN EL AIRE APENAS SUFREN VARIACIÓN, CON LO QUE SE CONSIDERA QUE EN EL AIRE LA VELOCIDAD DE LAS ONDAS ELECTROMAGNÉTICAS ES LA MISMA QUE EN EL VACÍO.

CUANDO UNA ONDA PASA DE UN MEDIO A OTRO DE ÍNDICE DE REFRACCIÓN DIFERENTE, CAMBIA SU VELOCIDAD, PERO SU FRECUENCIA NO CAMBIA, YA QUE EL FRENTE DE ONDA REFRACTADO SUSTITUYE INMEDIATAMENTE AL FRENTE DE ONDA INCIDENTE. COMO c=λ·f ; CAMBIARÁ SU LONGITUD DE ONDA.

CUESTIÓN F2BE2708:

Un rayo láser pasa de un medio a otro con un índice de refracción menor. Indicar si el ángulo de refracción será mayor o menor que el de incidencia. Argumentar la respuesta.

EJERCICIO F2BE2709:

Un rayo de luz incide desde el vidrio (n=1,6) sobre una superficie de separación con el aire.

a.- Hallar el ángulo de refracción si el ángulo de incidencia es de 25º.

b.- Hallar el ángulo límite.

c.- ¿Se producirá reflexión total para un ángulo de incidencia de 40º?

DATO: n_aire=1

42,55; 38,68; si

CUESTIÓN F2BE2710:

Justificar la expresión c=λ·f

EJERCICIO F2BE2711:

Un foco emite luz de 1,4 MHz en el vidrio. Hallar la longitud de onda en el aire y en este tipo de vidrio.

DATOS: 1 MHz=10⁶ Hz; n_vidrio=1,6; c=3·10⁸ m/s; n_aire=1

214,29 m; 133,93 m

EJERCICIO F2BE2712:

Determina la frecuencia de las radiaciones cuyas longitudes de onda son 630 y 490 nm. ¿A qué zona del espectro electromagnético pertenecen?

CONSULTA LA RED PARA LOCALIZAR LA ZONA DEL ESPECTRO

DATOS: c=3·10⁸ m/s; 1 nm= 10^-9 m

EJERCICIO F2BE2713:

Un rayo de luz de 450 nm de longitud de onda incide desde el aire sobre un material transparente con un ángulo de 40º con la normal y se refracta con un ángulo de 20º.

a.- Hallar el índice de refracción del material.

b.- Hallar la velocidad de la luz en el material.

c.- Hallar la longitud de onda en el material.

DATOS: 1 nm= 10^-9 m; n_aire=1;

1,88; 1,6·10⁸ m/s; 2,4·10^-7 m

EJERCICIO F2BE2714:

Hallar el ángulo límite para la luz que pasa de cierto material con n=1,7 al aire.

DATO: n_aire=1

36,03º

EJERCICIO F2BE2715:

Hallar el ángulo límite para la luz que pasa del aire a cierto material con n=1,7.

DATO: n_aire=1

EJERCICIO F2BE2716:

Un rayo de luz incide desde el vidrio (n=1,32) sobre una superficie de separación con el aire. Determina:

El ángulo de refracción si el de incidencia es de 30°.
El ángulo límite.
Indicar razonadamente si se producirá reflexión total para un ángulo de incidencia de 45°.

SOLUCIÓN: 41,3º; 49,25º; No

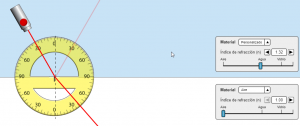
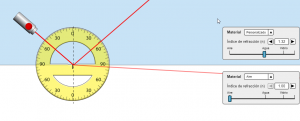
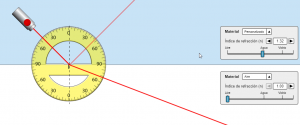
CAPTURAS DE PANTALLA DE LA APLICACIÓN PHET.COLORADO.EDU QUE PUEDEN AYUDAR A ENTENDER LA SITUACIÓN DEL EJERCICIO:

https://phet.colorado.edu/sims/html/bending-light/latest/bending-light_all.html?locale=es

EJERCICIO F2BE2717:

La velocidad de la luz en el agua es de 225000 Km/s ¿cuál es el índice de refracción absoluto del agua?

SOL.: n=1,33

EJERCICIO F2BE2718:

Un haz de luz incide sobre la superficie del agua con un ángulo de 45°. Si el índice de refracción de la luz en el aire es de 1 y en el agua es 1,33. ¿Cuánto miden los ángulos de reflexión y refracción?

SOL.: re= 45°; r=32°1’

DIOPTRIO PLANO:

ECUACIÓN DEL DIOPTRIO PLANO. ÓPTICA GEOMÉTRICA PARA FÍSICA DE BACHILLERATO

EJERCICIO F2BE2027:

Hallar la profundidad que parece tener una moneda que se encuentra sumergida en el fondo de una piscina de 5 m de profundidad.

Datos de índices de refracción:
Índice de refracción del aire: n_aire = 1; Índice de refracción del agua: n_agua = 1.333

IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIOS RESUELTOS DE APLICACIÓN DEL DIOPTRIO PLANO. ÓPTICA GEOMÉTRICA PARA FÍSICA DE BACHILLERATO

EJERCICIO F2BE2028:

Un pescado que se halla sumergido en el mar a una profundidad de 5 m percibe que un pescador que se encuentra en lo alto de un acantilado está a 50 m de él. Determinar la altura sobre el nivel del mar a la que realmente se encuentra el pescador.

Datos de índices de refracción:
Índice de refracción del aire: n_aire = 1; Índice de refracción del agua: n_agua = 1.333

IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EJERCICIOS RESUELTOS DE APLICACIÓN DEL DIOPTRIO PLANO. ÓPTICA GEOMÉTRICA PARA FÍSICA DE BACHILLERATO

ESPEJOS:

TRAZADO DE RAYOS EN ESPEJOS, CONSTRUCCIÓN DE IMÁGENES EN ESPEJOS:

De todos los rayos que emite un punto objeto y que al llegar al espejo se reflejan, hay tres cuya trayectoria se puede predecir, con lo que se puede formar fácilmente la imagen:

1.- Rayo que procedente del objeto llega paralelo al eje óptico, tras reflejarse en el espejo, lleva la dirección del foco imagen.

2.- Rayo que lleva la dirección del foco objeto, tras reflejarse en el espejo sigue una dirección paralela al eje óptico.

3.- Rayo que pasa por el centro óptico del espejo no modifican la dirección en la que se propaga.

EJERCICIO F2BE3004:

Disponemos de un espejo cóncavo de 1,2 metros de radio. Colocamos un objeto de 30 cm de alto a una distancia de 2,6 metros del espejo.

a.- Dibujar el trazado de rayos, para contrastar los cálculos posteriores.

b.- Hallar la distancia imagen.

c.- Hallar la altura de la imagen.

d.- Indicar las características de la imagen.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIOS RESUELTOS DE ESPEJOS ESFÉRICOS. ÓPTICA GEOMÉTRICA PARA FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE3005:

Disponemos de un espejo convexo de 1,2 metros de radio. Colocamos un objeto de 40 cm de alto a una distancia de 1,6 metros del espejo.

a.- Dibujar el trazado de rayos, para contrastar los cálculos posteriores.

b.- Hallar la distancia imagen.

c.- Hallar la altura de la imagen.

d.- Obtener el aumento lateral.

e.- Indicar las características de la imagen.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIOS RESUELTOS DE ESPEJOS ESFÉRICOS. ÓPTICA GEOMÉTRICA PARA FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE3007:

Disponemos de un espejo cóncavo de 60 cm de radio. Colocamos un objeto de 15 cm de alto a una distancia de 1,8 metros del espejo.

a.- Hallar la distancia imagen.

b.- Hallar la altura de la imagen

c.- Hallar el aumento lateral

d.- Indicar las características de la imagen.

e.- Dibujar el trazado de rayos, para contrastar los cálculos realizados

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE ELECTROMAGNETISMO Y ÓPTICA. TERCERA PRUEBA DEL SEGUNDO TRIMESTRE DEL CURSO 2024-25

EJERCICIO F2BE2029:

Disponemos de un espejo esférico de radio de curvatura, R= – 60 cm (según el criterio de signos de las normas DIN). Delante del espejo a 80 cm del espejo se dispone un objeto que tiene 10 cm de altura.

a.- Hallar la distancia a la que se formará la imagen.

b.- Realizar el diagrama de rayos correspondiente.

c.- Indicar las características de la imagen

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIOS RESUELTOS DE ESPEJOS ESFÉRICOS. ÓPTICA GEOMÉTRICA PARA FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE1300:

Un espejo esférico cóncavo ha de formar una imagen invertida de un objeto en forma de lápiz sobre una pantalla situada a una distancia de 420 cm delante del espejo. El objeto mide 5 mm y la imagen ha de tener una altura de 30 cm. Determinar:

a) A qué distancia del espejo debe colocarse el objeto.

b) El radio de curvatura del espejo.

c) Efectuar la construcción geométrica de la citada imagen.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIOS RESUELTOS DE ESPEJOS ESFÉRICOS. ÓPTICA GEOMÉTRICA PARA FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE129:

El radio de curvatura de un espejo cóncavo es de 20 cm. Un cuerpo está situado a 60 cm del espejo.

a.- ¿A qué distancia se formará la imagen?

b.- Indicar el foco y el aumento lateral.

c.- Realizar el trazado de rayos, indicando las características de la imagen.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIOS RESUELTOS DE ESPEJOS ESFÉRICOS. ÓPTICA GEOMÉTRICA PARA FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE131:

El espejo retrovisor de un automóvil es esférico y convexo y tiene un radio de curvatura de 1,5 metros. El conductor mira a través del espejo y observa un coche que se encuentra a 50 m de distancia. Si el coche tiene una altura de 1,4 metros, ¿cuál será el tamaño de la imagen del coche reflejada en el espejo?. Realizar el trazado de rayos, indicando las características de la imagen.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIOS RESUELTOS DE ESPEJOS ESFÉRICOS. ÓPTICA GEOMÉTRICA PARA FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE3012:

Disponemos de un espejo convexo de 50 cm de radio. Colocamos un objeto de 25 cm de altura a una distancia de 110 cm del espejo. Para esta situación se pide:

a.- Hallar la distancia imagen.

b.- Hallar la altura de la imagen.

c.- Hallar el aumento lateral.

d.- Realizar el trazado de rayos, haciendo el dibujo de la situación a escala 1:10, del siguiente modo:

d₁.- Dibujar la trayectoria del rayo que viene del infinito.

d₂.- Dibujar la trayectoria del rayo que lleva la dirección del foco objeto.

d₃.- Formar exclusivamente con los dos rayos anteriores la imagen, como corresponda.

d₄.- Con el rayo del apartado d₁, comprobar que se cumple la ley de Snell de la reflexión, utilizando el transportador de ángulos, indicando los ángulos que intervienen, en el dibujo y claramente.

e.- Indicar las características de la imagen, justificándolas, tanto analíticamente (con los resultados numéricos obtenidos) como geométricamente cuando corresponda.

IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: TRABAJO TRIMESTRAL DE ÓPTICA GEOMÉTRICA, PARA FÍSICA DE 2º BACHILLERATO. SEGUNDO TRIMESTRE DEL CURSO 2024-25

LENTES:

LENTES. ECUACIÓN FUNDAMENTAL DE LAS LENTES DELGADAS
FOCOS Y DISTANCIAS FOCALES EN LAS LENTES. POTENCIA DE UNA LENTE. CONSTRUCCIÓN DE IMÁGENES EN LAS LENTES
TIPOS DE LENTES habituales en ejercicios de óptica geométrica para Física de Bachillerato.

CONSTRUCCIÓN DE IMÁGENES EN LAS LENTES DELGADAS:

De todos los rayos que emite un punto objeto y que al atravesar una lente se refractan, hay tres cuya trayectoria se puede predecir, con lo que se puede formar fácilmente la imagen:

1.- Rayo que procedente del objeto llega paralelo al eje óptico, tras refractarse y atravesar la lente, pasa por el foco imagen.

2.- Rayos que llevan la dirección del foco objeto, al atravesar la lente sigue una dirección paralela al eje óptico.

3.- Rayos que pasan por el centro óptico de la lente no modifican la dirección en la que se propaga.

CONSTRUCCIÓN IMÁGENES LENTES DELGADAS_v1

EJERCICIO F2BE2047:

El robot Fénix-1 utiliza una cámara para fotografiar el suelo del planeta Hermione. La focal de la lente es 20 cm:

a.- Indicar el tipo de lente.

b.- Hallar la potencia de la lente.

c.- Hallar la posición de la imagen de un objeto situado a 35 cm de la cámara.

d.- Hallar la altura de la imagen de un objeto situado a 35 cm de la cámara que tiene una altura de 25 cm.

e.- Indicar las características de la imagen del objeto que se menciona en el apartado anterior.

f.- Para la situación descrita dibujar el trazado de rayos correspondiente.

Enlace al vídeo donde se resuelve este ejercicio: https://youtu.be/bm3wYmTnc0g

EJERCICIO F2BE2431: Ejercicio de lente desconocida

Dentro de un telescopio antiguo nos hemos encontrado con una lente. Haciendo pruebas hemos visto que forma la imagen de un objeto de 10 cm de alto, que se encuentra a 30 cm de la lente, a una distancia de 7,5 cm de la lente. La imagen que se forma está derecha.

a.- Hallar la altura de la imagen.

b.- El tipo de lente y su potencia.

c.- Las distancias focales.

d.- Las características de la imagen

e.- Realizar el trazado de rayos correspondiente.

SOLUCIÓN: 0,025 m; Divergente, -10 D; -0,1 m, 0,1 m; menor, virtual, derecha

VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/pkOJqB4rO1w

EJERCICIO F2BE2432:

Un objeto de 40 cm de altura se encuentra a 1,80 m de una lente de +1 dioptría. Hallar:

a.- La posición donde se forma la imagen.

b.- La altura de la imagen.

c.- Las características de la imagen.

d.- La posición del foco objeto y del foco imagen.

e.- Realizar el trazado de rayos correspondiente para la situación descrita.

f.- Indicar el tipo de lente, la potencia de la misma y su aumento lateral.

IR AL ARTÍCULO QUE CONTIENE LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE FÍSICA PARA 2º BACHILLERATO: NUCLEAR, ONDAS, GRAVITACIÓN, ÓPTICA

EJERCICIO F2BE2433:

Para una lente de distancia focal +10 cm, indicar las características de la imagen cuando el objeto se encuentra a una distancia de 15 cm de la lente. Obtener el aumento lateral y la distancia donde se forma la imagen.

SOLUCIÓN: Mayor, real, invertida; -2; 0,3 m

EJERCICIO F2BE2753:

Disponemos de una lupa de 6,67 D. Para esta realidad:

a.- Hallar la distancia de la lupa a la que debe situarse un objeto de 2,5 mm de altura para que forme la imagen a 30 cm de la lupa.

b.- Hallar el tamaño de la imagen, así como el aumento de la lupa en esta situación.

PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE ARTÍCULO: INTRUMENTOS ÓPTICOS. ÓPTICA GEOMÉTRICA: CÁMARA OSCURA, CÁMARA FOTOGRÁFICA, LUPA, MICROSCOPIO, TELESCOPIO.

SOLUCIÓN: 10 cm; 7,5 mm; 3

EJERCICIO F2BE2434:

Para una lente de distancia focal +10 cm, indicar las características de la imagen cuando el objeto se encuentra a una distancia de 7,5 cm de la lente. Obtener el aumento lateral y la distancia donde se forma la imagen.

SOLUCIÓN: Mayor, virtual, derecha; 4; -0,3 m

EJERCICIO F2BE2435: Ebau Canarias 2021

Un objeto de 2,5 cm de alto está situado a 0,75 cm de una lente. La imagen formada es de 4 cm de alto.

a.- ¿A qué distancia de la lente se forma la imagen del objeto?

b.- ¿Cuánto valen la distancia focal y la potencia de la lente? ¿Se trata de una lente convergente o divergente? Razone su respuesta.

c.- Dibuje el trazado de rayos y determine la posición a la que debe situarse el objeto, respecto de la lente, para que su imagen se forme en el infinito.

NOTA: En el dato que la imagen es de 4 cm de alto, va implícito que esa imagen es derecha, tenerlo en cuenta, ya que es un dato de relevancia y oculto.

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA DE EXAMEN RESUELTA DE FÍSICA DE 2º BACHILLERATO: GRAVITATORIO, ELECTROMAGNETISMO, ÓPTICA Y NUCLEAR. PRIMERA PRUEBA DEL TERCER TRIMESTRE DEL CURSO 2024-25

EJERCICIO F2BE2436: Ebau Canarias 2021

Una lente convergente de distancia focal +16 cm proyecta la imagen nítida de un objeto, de 3 cm de alto, sobre una pantalla que se encuentra a 4 m de la lente.

a.- Dibuje el diagrama de rayos de la situación planteada.

b.- ¿A qué distancia de la lente está colocado el objeto?

c.- ¿Cuál es el aumento lateral de la imagen y la potencia de la lente?

EJERCICIO F2BE2437:

Un proyector de diapositivas, con una distancia focal de +15 cm, proyecta la imagen nítida de una diapositiva de 3,5 cm de alto, sobre una pantalla que se encuentra a 4 metros de la lente.

a.- Indicar la distancia a la que está colocada la diapositiva de la lente.

b.- Hallar el tamaño de la imagen.

c.- Obtener el aumento de la lente en esta situación.

SOLUCIÓN: -0,156 m; -0,9 ;-25,6

EJERCICIO F2BE2446:

Una lente de un microscopio aumenta el tamaño del objeto 5 veces. Se sabe que un objeto de 5 cm de alto colocado a 20 cm de la lente forma la imagen invertida.

a.- La altura de la imagen.

b.- La posición de la imagen.

c.- El tipo de lente y su potencia.

d.- Las distancias focales.

e.- Las características de la imagen.

f.- Realizar el trazado de rayos para la situación descrita.

SOLUCIONES: 0,25 m; 1 m; +6 D; ±0,167 m; Real, mayor tamaño, invertida

EJERCICIO F2BE2447:

Una lente forma la imagen invertida de un objeto de 5 cm de alto, que se encuentra a 20 cm de la lente, a una distancia de 5 cm de la lente. Obtener:

a.- La altura de la imagen.

b.- La posición de la imagen.

c.- El tipo de lente y su potencia.

d.- Las distancias focales.

e.- Las características de la imagen.

f.- Realizar el trazado de rayos para la situación descrita.

SOLUCIONES: 0,0125 m; +0,05 m; +25 D; ±0,04 m; Real, menor tamaño, invertida

IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIO DE ÓPTICA, DE LENTES, PARA FÍSICA DE 2º DE BACHILLERATO

EJERCICIO F2BE2048:

La miopía dificulta la visión de objetos lejanos y se corrige con una lente divergente que hace que el conjunto de lente y cristalino forma la imagen de un objeto lejano sobre la retina.

Disponemos de una lente divergente de una persona miope que tiene una potencia de -5 dioptrías.

a.- Hallar la distancia focal imagen de la lente.

b.- Hallar la posición de la imagen vista a través de la lente de un objeto situado a 1,5 m de la lente.

c.- Indicar las características de la imagen.

d.- Dibujar el trazado de rayos correspondiente.

Enlace al vídeo donde se resuelve este ejercicio: https://youtu.be/qWZ25_7bA34

EJERCICIO F2BE2438:

Hemos visto que una de las lentes de un microscopio aumenta el tamaño del objeto 5 veces. La lente forma la imagen invertida de un objeto de 5 cm de alto, que se encuentra a 20 cm de la lente a una distancia de 5 cm de la lente.

a.- La altura de la imagen.

b.- La posición de la imagen.

c.- El tipo de lente y su potencia.

d.- Las distancias focales.

e.- Las características de la imagen.

f.- Realizar el trazado de rayos para la situación descrita.

EJERCICIO PARA PENSAR, YA QUE EL DATO DEL AUMENTO CONTRADICE EL RESTO DE LOS DATOS. SE VALORARÁ CAER EN LA CUENTA DE ELLO. NO OBSTANTE EN LOS CASOS EN QUE NO SE CAIGA EN LA CUENTA DE LA FALTA DE COHERENCIA DE LOS DATOS, SE VALORARÁ EN FUNCIÓN DEL DATO DE PARTIDA ELEGIDO. INTERESANTE LA CONSULTA DE LAS SOLUCIONES.

SOLUCIÓN DEL EJERCICIO EN: PRUEBA DE EXAMEN DE FÍSICA DE 2º BACHILLERATO (X883)

EJERCICIO F2BE2772:

Para una lente de distancia focal +10 cm, y para un objeto de 3 cm de alto colocado a 2 cm de la lente. Obtener de forma analítica:

a.-Potencia de la lente y aumento lateral.

b.- Posición de la imagen.

c.- Tamaño de la imagen.

Realizar los cálculos aproximando al milímetro.

d.- Realizar el trazado de rayos (de los tres rayos significativos) utilizando un dibujo real, sin escalas, preferiblemente en papel milimetrado, contrastando los resultados obtenidos de posición de la imagen, altura de la imagen, y comentando las características de la imagen a través del dibujo y de los parámetros obtenidos.

e.- Si el mismo objeto se coloca a 4 cm de la lente, ¿el aumento lateral será el mismo?. Obtener el tamaño de la imagen en este caso.

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ÓPTICA Y CONTRASTE: TRABAJO TRIMESTRAL DE FÍSICA DE 2º BACHILLERATO. ELECTROSTÁTICA Y ÓPTICA

EJERCICIO F2BE3026: 31 Relación de óptica

Se dispone de una lente convergente (una lupa) de distancia focal f’=5 cm, que se utiliza para mirar sellos. Indica la distancia a la que hay que situar los sellos si se quiere obtener una imagen virtual:

a.- Diez veces mayor que el original.

b.- Veinte veces mayor que el original.

EJERCICIO F2BE3027: 32 Relación de óptica

Un objeto se encuentra situado a 1 m delante de una lente convergente de 2 dioptrías. Calcula:

a.- La posición de su imagen y el tipo de imagen formada a través de la lente.

b.- Repite el problema, pero suponiendo que los datos se refieren a una lente divergente.

EJERCICIO F2BE3028: 33 Relación de óptica

¿Qué tamaño tiene la imagen de la Luna observada por una lente convergente de distancia focal igual a 40 cm?. El diámetro de la Luna es de 3600 km. La distancia de la Tioerra a la Luna es de 380000 km.

EJERCICIO F2BE2444: X806

El satélite Suspendidus II, cuya principal función es el estudio de la evolución de la calima sobre Tenteniguada, dispone de una cámara que dispone de una lente de +5 D.

TAREA 1:

a.- Hallar la posición de la imagen de un objeto de 9 cm de alto colocado a una distancia de 30 cm de la lente.

b.- Hallar la altura de la imagen que se forma.

c.- Hallar el aumento lateral, indicando el significado del signo que resulta.

c.- Indicar las características de la imagen.

TAREA 2:

a.- Hallar la posición de la imagen de un objeto de 9 cm de alto colocado a una distancia de 40 cm de la lente. (1 punto)

b.- Hallar la altura de la imagen que se forma.

c.- Hallar el aumento lateral en este caso, indicando el significado del signo que resulta para el mismo.

d.- Indicar las características de la imagen.

TAREA 3:

Contrastar, representando a escala 1:10 las situaciónes de las dos tareas anteriores y realizando el trazado de rayos correcto.

TAREA 4:

Si la lente mencionada fuera biconvexa, de vidrio con n=1.33, con los radios de curvatura iguales en valor absoluto, hallar el valor de cada uno de los radios de la lente.

La puntuación se distribuye por igual entre las 4 tareas.

EJERCICIO F2BE1292:

Calcula el índice de refracción de una sustancia respecto del aire sabiendo que su ángulo límite es de 30º.

DATO: n_aire=1

SOLUCIÓN: 2

EJERCICIO F2BE1293:

a) Determinar el valor de ángulo de refracción correspondiente al ángulo de incidencia anterior.

b) Definir ángulo límite y calcular el valor para los dos medios anteriores.

SOL._ 19,46º; 51,12º

EJERCICIO F2BE1294:

Se coloca un objeto de 10 cm de altura a 0,2 m de una lente biconvexa de 2 dioptrias.

a) Obtener gráficamente la posición y tamaño de la imagen que resulta. ¿Es real o virtual?

b) Calcular analíticamente dichas posición y tamaño.

SOL.: -33,3 cm; 16,65 cm

EJERCICIO F2BE1295:

Se tiene una lente bicóncava con radios de curvatura de 20 y 40 cm. Su índice de refracción es de 1,8. Un objeto de 3 mm se coloca a 50 cm de la lente. Calcule:

a) La potencia óptica de la lente.

b) Dónde se forma la imagen.

c) El tamaño de la imagen.

SOLUCIÓN: -6 d; -0,125 m; 0,75 mm

EJERCICIO F2BE1296:

Una lente planoconvexa está hecha de un plástico con un índice de refracción de 1,7 y sus distancias focales son iguales a 40 cm. Calcular:

a) El radio de curvatura de la lente.

b) Distancia a la que focaliza un objeto de 2 mm de tamaño situado a 0,8 m de la lente.

c) Tamaño de la imagen producida por el objeto anterior.

SOLUCIÓN: 0,28 m; 0,8 m; -2 mm

EJERCICIO F2BE1297:

Una lente bicóncava simétrica posee una potencia óptica de -2 dioptrias y está formada por un plástico con un índice de refracción de 1,8. Calcule:

a) La velocidad de la luz en el interior de la lente.

b) Los radios de curvatura de la lente.

c) Donde hemos de colocar un objeto para que el tamaño de su imagen sea la mitad que el del objeto.

SOLUCIÓN: 1,7E8; 0,8 m; 0,5 m

EJERCICIO F2BE1298:

Un objeto luminoso de 2 mm de altura está situado a 4 m de distancia de una pantalla. Entre el objeto y la pantalla se coloca una lente esférica delgada, L, de distancia focal desconocida, que produce sobre la pantalla una imagen tres veces mayor que el objeto.

a) Determine la naturaleza de la lente L, así como su posición respecto del objeto y de la pantalla.

b) Calcule la distancia focal, la potencia de la lente L y efectúa la construcción geométrica de la imagen.

SOLUCIÓN: CONVERGENTE, -1 m; 3 m; 0,75 m

EJERCICIO F2BE1299:

Un objeto luminoso está situado a 6 m de una pantalla. Una lente, cuya distancia focal es deconocida, forma sobre la pantalla una imagen real, invertida y cuatro veces mayor que el objeto. Justificar con una diagrama de rayos qué tipo de lente es.

a) ¿Cuál es la posición de la lente y su distancia focal?

SOLUCIÓN: 1,2 m; 4,8 m; 0,96 m

EJERCICIO F2BE2092:

Por 5G se entiende en telecomunicaciones la quinta generación en tecnología de teléfonos móviles, que se pretende que para 2025 sustituya a la 4G. Las bandas más altas de la tecnología 5G se encuentran entre los 25 y 39 GHz, para alcanzar velocidades de descarga en el rango de los Gbit/s, similar a la que se alcanza con Internet por cable.

Suponiendo que un teléfono móvil funciona con ondas electromagnéticas de frecuencia 30 GHz:

Hallar el periodo, la longitud de onda y el número de onda en el aire.
Si resulta que la onda entra en un medio en el que su velocidad sufre una disminución, reduciéndose al 85% de su velocidad, obtener los valores de la frecuencia y la longitud de onda en ese nuevo medio.
Hallar el índice de refracción del nuevo medio.

DATOS: 1 GHz=10⁹ Hz; c=3·10⁸ m/s; n_aire=1

Enlace al vídeo donde se resuelve el ejercicio: https://youtu.be/H9bZIYmmSW8

EJERCICIO F2BE2093:

Un rayo láser es radiación electromagnética, que con un sistema de amplificación de la luz produce rayos de enorme intensidad. El rayo láser visible tiene longitudes de onda de 400 a 700 nm. No es un juguete y puede producir daños en el ojo irreversibles, así como en la piel.

Se hace incidir un rayo láser cuya longitud de onda en el aire es de 520 nm sobre un trozo de vidrio. Los rayos reflejados y refractados forman ángulos de 40^o y de 30^o respectivamente.

Hallar el índice de refracción del cristal y la longitud de onda de la luz láser en el interior del vidrio.

DATOS: 1 nm=10^-9 m; n_aire=1

Enlace al vídeo donde se resuelve el ejercicio: https://youtu.be/jNE-nPQq13c

DEFECTOS DEL OJO HABITUALES: MIOPÍA E HIPERMETROPÍA:

OJO NORMAL:

El ojo normal es una estructura casi esférica de unos 2,5 cm de diámetro.

EL PUNTO REMOTO ES EL PUNTO MÁS LEJANO QUE SE PUEDE VER CON NITIDEZ. En un ojo normal a partir de 5 o 6 metros todo te aparece enfocado, incluso objetos muy lejanos como las estrellas, con lo que en ojos normales el punto remoto está en el infinito.

EL PUNTO PRÓXIMO ES EL PUNTO MÁS CERCANO AL OJO QUE PUEDE VERSE CON NITIDEZ. EN UN OJO NORMAL ESTÁ ENTRE 15 Y 20 CM. (no ves bien más cerca de esa distancia)

EL OJO DE UNA PERSONA CON VISTA NORMAL (EMÉTROPE) PUEDE VER CON NITIDEZ LOS OBJETOS ENTRE ESOS DOS PUNTOS.

CRISTALINO Y MÚSCULOS CILIARES:

LA LENTE DEL INTERIOR DEL OJO ES EL CRISTALINO, QUE ES UNA LENTE BICONVEXA QUE PUEDE MODIFICAR SU CURVATURA CON LOS MÚSCULOS CILIARES. Cuando el objeto que pretendemos ver se acercan al ojo los músculos ciliares se tensan y contraen el cristalino, lo que aumenta su curvatura y reduce su distancia focal, para que la imagen se forma nítidamente en la retina. Este proceso se llama acomodación.

OJO MIOPE:

EL OJO MIOPE TIENE EL PUNTO REMOTO MUY CERCANO (ESTÁ A UNA DISTANCIA FINITA). NO VÉ BIEN LOS OBJETOS ALEJADOS. FORMA LA IMAGEN DELANTE DE LA RETINA.

PUEDE SER DEBIDO A QUE EL OJO ES DEMASIADO PROFUNDO O PORQUE EL CRISTALINO TIENE DEMASIADA CURVATURA.

PARA CORREGIR LA MIOPÍA LA LENTE DEBE FUNCIONAR DE MODO QUE EL INFINITO TE LO ACERQUE AL PUNTO REMOTO, QUE ES EL PUNTO MÁS ALEJADO QUE VE CON NITIDEZ. SE CORRIGE CON UNA LENTE DIVERGENTE.

ES CONVERTIR EL PUNTO REMOTO EN EL FOCO DE LA LENTE.

POR ELLO f´= – Punto remoto , (lente divergente, foco negativo) y sus dioptrías P=1/f´

OJO HIPERMÉTROPE:

EL OJO CON HIPERMETROPÍA TIENE EL PUNTO PRÓXIMO MÁS ALEJADO DE LO NORMAL. FORMA LA IMAGEN DETRÁS DE LA RETINA.

PUEDE SER PORQUE EL OJO ES POCO PROFUNDO O A QUE LA CÓRNEA O EL CRISTALINO TIENEN UNA POTENCIA ÓPTICA DISMINUIDA.

PARA CORREGIR LA HIPERMETROPÍA LA LENTE DEBE FUNCIONAR DE MODO QUE LA IMAGEN TE LA COLOQUE EN EL PUNTO PRÓXIMO DEL OJO, QUE ES EL PUNTO MÁS CERCANO QUE VÉ CON NITIDEZ. SE CORRIGE CON UNA LENTE CONVERGENTE.

ES CONVERTIR LA IMAGEN DE UN OBJETO CERCANO EN SU PUNTO PRÓXIMO.

OJO PRÉSBITA (PRESBICIA):

ES LA PÉRDIDA DE CAPACIDAD DE ACOMODACIÓN QUE SUFREN LAS PERSONAS CON LA EDAD, POR RIGIDEZ DEL CRISTALINO (PÉRDIDA DE FLEXIBILIDAD), SE CONOCE COMO VISTA CANSADA.

EL PUNTO PRÓXIMO SE ALEJA Y SE DIFICULTA LA VISIÓN A DISTANCIAS CORTAS.

SE CORRIGE CON LENTES CONVERGENTES QUE LLEVAN LA IMAGEN DEL OBJETO AL PUNTO PRÓXIMO DE LA PERSONA.

ASTIGMATISMO:

Las personas que lo presentan tienen habitualmente la córnea deformada, con una curvatura vertical diferente de la horizontal, como un balón de rugby, frente a la situación normal esférica, lo que produce que no se enfoquen correctamente ni los objetos cercanos ni los lejanos. Se corrige con lentes cilíndricas.

EJERCICIO F2BE2526, DEL COMPORTAMIENTO DEL CRISTALINO COMO LENTE Y SU TRATAMIENTO DESDE LA ÓPTICA GEOMÉTRICA:

El ojo humano se puede considerar como un sistema óptico con una lente, el cristalino, en un extremo del globo ocular (para este estudio de 15 mm de diámetro) y en el otro extremo la retina (donde deben formarse las imágenes de objetos lejanos para ser percibidas con nitidez). Hallar:

a.- La potencia del cristalino que estamos considerando y confirmar el tipo de lente que es.

b.- Suponiendo que este cristalino se mantiene sin acomodación, hallar la posición de la imagen de un objeto situado a 60 m del cristalino e indicar si se va a percibir con nitidez.

c.- Hallar el tamaño de la imagen de una farola de 8 m de altura que se encuentra a 80 m del ojo, e indicar si se va a percibir con nitidez.

d.- Hacer comentarios sobre los valores de la distancia imagen de los apartados b y c.

NOTA: La exactitud, en virtud de los datos, debe ser al milímetro.

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO Y OTROS DE INTERÉS PARA FÍSICA DE 2º DE BACHILLERATO: EXAMEN RESUELTO DE FÍSICA DE 2º DE BACHILLERATO: CAMPO ELECTROSTÁTICO, MAGNÉTICO, ONDAS, RELATIVIDAD, CUÁNTICA, ÓPTICA Y DEFECTOS DEL OJO.

EJERCICIOS F2BE2094 Y F2BE2095, LA MIOPÍA Y LA HIPERMETROPÍA ENFRENTADAS:

EJERCICIO F2BE2094:

Un ojo miope se comporta de modo que el punto remoto está a 50 cm. ¿Qué lente se necesita para corregir esto?.

INDICACIÓN: La lente para corregir el defecto debe formar la imagen del infinito (punto remoto normal) en el punto remoto de la persona con miopía.

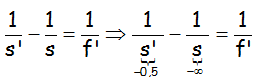
EJERCICIO F2BE2095:

El punto próximo de una persona se encuentra a 1,20 metros de distancia. Indicar la alteración que presenta su ojo, la lente que la puede corregir y las dioptrias de las gafas que le permitirían poder leer a 25 cm de distancia.

INDICACIÓN: La lente debería colocar la imagen del libro en el punto próximo del ojo.

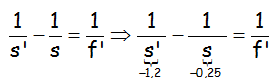
IR AL VÍDEO QUE RESUELVE LOS DOS EJERCICIOS: https://youtu.be/BLtL3ESsc5c

EJERCICIO F2BE2519:

Una persona de 57 años con presbicia ha comprobado que su punto próximo está a 80 cm.

a.- ¿Podrá leer con comodidad a 25 cm?

b.- Indicar el tipo de lentes y la potencia de las gafas que necesita para poder leer a esos 25 cm del apartado anterior.

SOLUCIÓN: P=2,75 D

CUESTIONES CORTAS F2BE2520:

A.- ¿Por qué las personas mayores llevan gafas para leer?.

B.- ¿Por qué vemos a personas mayores que para leer en el supermercado las calorías del yogur se lo alejan estirando la mano?.

C.- ¿Por qué se dice que un miope es «corto de vista»?

D.- ¿Por qué se le dice a la presbicia «vista cansada»?

E.- ¿Qué sufren los alumnos que no ven bien la pizarra en clase?, ¿cómo puede corregir este defecto de la vista?.

F.- ¿Por qué un hipermétrope y un presbita utilizan lentes convergentes y un miope divergentes?

EJERCICIO F2BE2521:

Un individuo con miopía constata que tiene su punto remoto a 16,7 cm. Hallar la potencia e indicar el tipo de las lentes que necesita para poder ver objetos situados en el infinito.

SOLUCIÓN: -6 D

EJERCICIO F2BE2522:

El punto remoto de cierta persona está a 6 m. Hallar:

a.- La lente que necesita para ver el infinito sin acomodación y la potencia de la lente.

b.- ¿Qué defecto óptico puede presentar la persona?

EJERCICIO F2BE2523:

Un alumno no ve claramente los objetos situados más alejados de 2,5 m, su punto remoto. Hallar:

a.- La dolencia de su vista.

b.- La distancia focal de las lentes que debe utilizar para corregir ese defecto óptico.

c.- El tipo de lentes.

d.- La potencia de las lentes.

SOLUCIÓN: -0,4 D

EJERCICIO F2BE2524:

El cristalino del ojo humano se puede considerar una lente. Si el diámetro del globo ocular de un determinado ojo es de 25 mm, hallar la potencia y la distancia focal del cristalino cuando lees las calorías de una lata de atún desde 55 cm de distancia; indicar además el tipo de lente que es el cristalino.

EJERCICIO F2BE2527:

Sabemos que el ojo de una persona se comporta de modo que tiene el punto remoto a 75 cm.

a.- Indicar el tipo de defecto que tiene, el tipo de lentes que debe usar y la potencia de la lente que corregiría el problema (explicando el proceso).

b.- Con la lente que corrige su problema, hallar la posición de la imagen de un objeto de 25 cm de alto que se coloca a 1 m de la lente, realizando el trazado de rayos correspondiente, e indicando las características de la imagen.

INTERESA LA CONSULTA DEL SIGUIENTE ARTÍCULO:

INTRUMENTOS ÓPTICOS. ÓPTICA GEOMÉTRICA

PODRÍA INTERESAR LA VISITA AL SIGUIENTE ARTÍCULO DEL PROYECTO, DONDE SE DESARROLLAN LAS ASIGNATURAS DE FÍSICA Y QUÍMICA DE SECUNDARIA Y BACHILLERATO:

FÍSICA Y QUÍMICA DE SECUNDARIA (E.S.O.) Y BACHILLERATO: DESARROLLO DE LAS ASIGNATURAS

Post Views: 6.141