CINEMÁTICA MOVIMIENTOS MRU PARABÓLICO

FÍSICA Y QUÍMICA 1º BACHILLERATO

CINEMÁTICA, MOVIMIENTOS: DE MRU A PARABÓLICO:CINEMÁTICA MOVIMIENTOS MRU PARABÓLICO

En Física y Química de 1º de Bachillerato, con frecuencia, la dificultad que nos encontramos es la de Homogeneizar contenidos de Física entre los alumnos, para poder trabajar los contenidos propios de este nivel.

A los Institutos Diocesanos, para 1º de Bachillerato, nos llegan alumnos de varios centros diferentes, todos ellos muy bien preparados y los esfuerzos iniciales se basan en uniformar contenidos previos.

Entendemos, después de reflexionar dentro del proyecto Achimagec, que hay que trabajar cuanto antes la composición de movimientos, el MOVIMIENTO PARABÓLICO y a través de él lo que es relevante de las cuestiones VECTORIALES que tanto tiempo nos llevan en este nivel.

El documento que se ofrece contiene lo que el alumno debería conocer, pero que no siempre conoce:

Los MOVIMIENTOS RECTILÍNEOS UNIFORMES (M.R.U.), los MOVIMIENTOS RECTILÍNEOS UNIFORMEMENTE ACELERADOS (M.R.U.A.), la aplicación del anterior al MOVIMIENTO DE CAÍDA LIBRE (MOVIMIENTO VERTICAL) EN LAS PROXIMIDADES DE LA SUPERFICIE TERRESTRE, con el objetivo de que podamos llegar cuanto antes al MOVIMIENTO PARABÓLICO (TIRO OBLICUO o COMPOSICIÓN DE MOVIMIENTOS).

Interesa al respecto, si los conocimientos previos no son los suficientes, los siguientes artículos de este mismo proyecto:

Con respecto a la cuestión de las MAGNITUDES VECTORIALES DEL MOVIMIENTO, para aterrizar en un caso concreto en el que se aplica y ahorrar todo el tiempo que lleva esta cuestión, proponemos el ejercicio 22 de MOVIMIENTO PARABÓLICO, que contiene los aspectos de mayor continuidad en esto del CÁLCULO VECTORIAL.

La propuesta que hacemos desde Achimagec, en la línea de optimizar el tiempo de una asignatura cargada de contenido y con falta de tiempo, es por lo tanto, intentar llegar cuanto antes al MOVIMIENTO PARABÓLICO, que al fin y al cabo contiene los movimientos anteriores, que son repasados mientra lo tratamos específicamente. Se añade en algunos casos un refuerzo a la COMPETENCIA DIGITAL, utilizando aplicaciones al alcance para el contraste gráfico de lo obtenido analíticamente, sobre todo en los casos de la ECUACIÓN DE LA TRAYECTORIA del MOVIMIENTO PARABÓLICO.

Con motivo de facilitar el acceso al aprendizaje, durante los periodos de inasistencia por causa del COVID-19, hemos realizado una serie de videos que resuelven los ejercicios propuestos.

ASPECTOS FORMALES PARA DOCENTES, ACTUALIZADOS A LA LOMLOE, AL FINAL DEL ARTÍCULO, PARA NO INTERFERIR CON LO QUE TIENE INTERÉS PARA EL APRENDIZAJE DE LOS ALUMNOS.

MOVIMIENTO PARABÓLICO:

Comenzamos lanzando una bola de papel a algún alumno, preferiblemente que esté distraído, y generamos largo rato apertura de opiniones al respecto de lo observado y características del movimiento. Quizás en algún momento haya que orientar.

MOVIMIENTO PARABÓLICO, INTRODUCCIÓN TEÓRICA: 

https://youtu.be/9bAEBRBvV8U

MOVIMIENTO PARABÓLICO, CONCRETAMENTE LA DESCOMPOSICIÓN DE LA VELOCIDAD INICIAL, EN CADA UNO DE LOS EJES, PARA OBTENER LA VELOCIDAD INICIAL EN X Y EN Y, UTILIZANDO LA TRIGONOMETRÍA:

https://youtu.be/5kSv46Arq6k

EJERCICIO FQ1BE2063, EJERCICIO DE EJEMPLO:

Lanzamos una piedra hacia el mar, desde lo alto de un acantilado de 100 metros de alto con una velocidad de 15 m/s formando un ángulo de 30º con la horizontal. En esta situación se pide:

a.- Hallar el tiempo que tarda en llegar al agua.

b.- Hallar el alcance máximo.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/F4WNbfmBRgc

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: PRUEBA TRUEQUE (EXAMEN DE MEJORA) DE FÍSICA PARA FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO

EJERCICIO FQ1BE2294:

Un camión de bomberos tiene en su parte superior, a 5 metros del suelo, una lanzadera de agua, con la que consigue lanzar un chorro de agua formando 300 con la horizontal.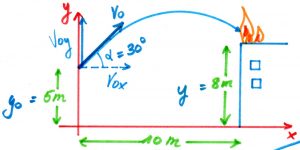MOVIMIENTO PARABÓLICO MANGUERA CAMIÓN BOMBEROS

En un momento dado en un edificio a 10 metros del camión y a una altura de 8 metros en la fachada del edificio, hay un incendio. Qué velocidad debe tener el chorro de agua para poder apagarlo?.

DATO: Utilizar el valor de la aceleración de la gravedad g=9,8 m/s2.

IR AL VÍDEO CON LA RESOLUCIÓN DEL EJERCICIO: https://youtu.be/XzUBBLyAcvw

EJERCICIO FQ1BE2295: «mismas estrategias que el ejercicio anterior»

Alejandra se ofrece voluntaria para que Alberto practique el tiro con arco al estilo de Guillermo Tell. Para ello Alejandra coloca una manzana encima de su cabeza, a 1,70 metros de altura, situándose ella misma a 10 m de Alberto.

Sabiendo que la flecha sale con un ángulo de 30º con la horizontal y desde una altura de 1,80 metros. Hallar la velocidad de la flecha para que impacte en la manzana.

DATO: g=9,8 m/s2.

EJERCICIO FQ1BE2065:

EJERCICIO QUE RESPONDE A PREGUNTAS DE CINEMÁTICA VECTORIAL, A TRAVÉS DEL MOVIMIENTO PARABÓLICO

Con un tirachinas y desde una altura sobre el suelo de 1,8 m, un joven lanza una piedra con una velocidad de 21 m/s formando un ángulo de 30º con la horizontal.

a.- Obtener la expresión del vector de posición de la piedra en función del tiempo.

b.- Obtener el vector velocidad para cualquier instante de tiempo.

c.- Hallar el vector desplazamiento total (entre la posición inicial y la final).

DATO: g = 9,8 m/s2

IR AL VÍDEO QUE RESUELVE ESTE EJERCICIO: https://youtu.be/mMeDeAvZ6i0

EJERCICIO FQ1BE2300, CON ASPECTOS DE CINEMÁTICA VECTORIAL:

Desde una altura de un metro lanzamos un objeto con una velocidad de 5 m/s que forma un ángulo de 30º con la horizontal. Hallar:

a.- El alcance máximo.

b.- La altura máxima.

c.- El vector de posición inicial.

d.- El vector de posición final.

e.- El vector desplazamiento total.

f.- El vector velocidad final.

g.- El vector velocidad en el punto más alto de la trayectoria.

h.- El vector aceleración en tres puntos distintos de la trayectoria.

DATO: Considerar g = 9,8 m/s2

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/yAsX9T2J7N4

EJERCICIO FQ1BE2302:

Un joven irresponsable, temerario e inconsciente, inicia una carrera en el muelle Deportivo de Las Palmas de Gran Canaria, en un momento de marea baja, con el agua a 3 metros del borde del muelle con la intención de lanzarse. Suponiendo que la velocidad con la que abandona el muelle es de 6 m/s y horizontal. Hallar:

a.- El alcance máximo.

b.- El vector de posición inicial, lógicamente respecto al Sistema de Referencia que se elija.

d.- El vector de posición final.

e.- El vector desplazamiento total.

f.- El vector velocidad en el punto más alto de la trayectoria.

g.- El vector aceleración en tres puntos cualquiera y distintos de la trayectoria.

DATO: Considerar g = 9,8 m/s2

NOTA: Deseamos sinceramente que no se golpee con el fondo y queremos hacer constar que EN ESTOS CASOS DE IMPRUDENCIA, POR LO MENOS NO SE TIREN DE CABEZA.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/R8TnFOYsKJQ

EJERCICIO FQ1BE2301:

El Roque Nublo se levanta 80 metros sobre su base. Desde la parte más alta del Nublo lanzamos horizontalmente una piedra, con una velocidad del 15 m/s. Considerando el origen del sistema de referencia habitual (x=0 e y=80 en el lugar del disparo), responder a las siguientes cuestiones:

a.- Hallar el alcance horizontal máximo contado desde la base del Nublo que alcanza la piedra.

b.- Hallar el vector de posición inicial.

c.- Hallar el vector de posición final.

d.- Hallar el vector velocidad inicial.

e.- Hallar el vector velocidad final.

f.- Hallar el vector aceleración inicial.

g.- Hallar el vector aceleración final.

h.- Hallar el vector desplazamiento total.

i.- Hallar el vector de posición en t=1.

j.- Hallar el vector de posición en t=2.

k.- Hallar el vector desplazamiento entre los instantes t=1 y t=2.

DATO: g=9,8 m/s2.

EJERCICIO FQ1BE2315:

El Roque Nublo se levanta 80 metros sobre su base. Desde la parte más alta del Nublo lanzamos horizontalmente una piedra, con una velocidad del 15 m/s. Considerando el origen del sistema de referencia habitual (x=0 e y=0 en la base del Nublo. Para esta situación planteada:

a.- Obtener la ecuación de la trayectoria.

b.- Utilizarla para obtener la distancia horizontal, a la que la piedra pasa de la base del Nublo (alcance máximo si la base del Nublo se extendiera hasta ese punto).

c.- Realizar la representación en geogebra o similar para contrastar los resultados anteriores.

DATO: g=9,8 m/s2.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/vg08j6Vc7PU

EJERCICIO FQ1BE2316:

Desde una altura de un metro respecto del suelo, lanzamos un objeto con una velocidad de 15 m/s que forma un ángulo de 30º con la horizontal. Considerando el valor de g=9,8 m/s2, a lo largo de toda la experiencia, y eligiendo el sistema de referencia habitual (x=0 en el momento del lanzamiento, y=0 en el suelo) obtener:

a.- El vector de posición del objeto en función del tiempo.

b.- El vector de posición del objeto para t=1 s.

c.- El vector de posición del objeto para t=2 s.

d.- Interpretar el signo de la componente «y» del vector de posición en este último caso del apartado c, con todo lujo de detalles.

IR AL VÍDEO CON LA SOLUCIÓN DETALLADA DE ESTE EJERCICIO: https://youtu.be/8PNrwQpYyWc

NOTA: En el video al final se comete un error numérico, perdonable, juega a detectarlo, ya que no pienso subirlo de nuevo… 

EJERCICIO FQ2EE2068:

Lanzamos una piedra desde una altura de 1,8 m con un ángulo de lanzamiento de 30o, intentando que impacte con una sopladera que se encuentra a 3 m de distancia y a una altura de 70 cm.

¿Qué velocidad debemos comunicarle?

DATO: g=9,8 m/s2.

IR AL VÍDEO QUE RESUELVE ESTE EJERCICIO: https://youtu.be/BAwBCGL085w

EJERCICIO FQ1BE2069, nº 23-6 del archivo que se adjunta:

Desde la azotea de una casa que está a 50 m de altura, lanzamos horizontalmente un balón con una velocidad de 25 m/s. Despreciando el rozamiento con el aire, hallar:

a.- El punto donde caerá el balón al suelo.

b.- La velocidad con que llega al suelo.

c.- El tiempo que tarda en llegar al suelo.

d.- Hallar la ECUACIÓN DE LA TRAYECTORIA.

DATO: g=9,8 m/s2

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/tecuaUWS7IU

EJERCICIO F1BE2071, nº 23-5 del archivo que se adjunta en pdf al final de esta entrada:

Desde el suelo y con un ángulo de salida de 30º, se lanza un objeto con una velocidad de 8 m/s.

a.- Hallar la altura máxima que alcanza.

b.- Hallar el tiempo que tarda en alcanzar la altura máxima.

c.- Hallar el alcance máximo

d.- Hallar la ecuación de la trayectoria.

DATO: g=9,8 m/s2

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/ylyj83oJ3e8

EJERCICIO F1BE2248:

Un corredor despistado que está haciendo ejercicio en el Muelle de la luz cae al agua cuando va a una velocidad de 5,5 m/s. Las rocas se encuentran por debajo del nivel del muelle a 3 m, y llegan hasta 1,75 metros del borde del muelle.

a.- Chocará contra las rocas que hay debajo o caerá al agua.

b.- Hallar el vector de posición en t=1 s.

c.- Hallar el vector desplazamiento total.

d.- Hallar la velocidad final, vector y módulo.

EJERCICIO FQ1BE2294:

Desde el acantilado de Faneque, por encima del «dedo de Dios», a una altura de aproximadamente 1050 m, un irresponsable lanza una piedra con una velocidad inicial de 20 metros por segundo que forma un ángulo de 30º con la horizontal. Hallar la distancia a la que cae la piedra medida desde el borde del acantilado. Por cierto: el acantilado de Faneque es el más alto de España y el 7º del mundo.

DATO: utilizar el valor de g=9,8 m/s2.

EJERCICIO FQ1BE2314: «El saltamontes y la cantonera»

Un cigarrón se dispone a saltar desde el borde de una cantonera. El saltamontes conoce que el alcance máximo lo consigue iniciando el salto con un ángulo de salida de 45º. Por su edad y complexión la velocidad de salida que consigue en el salto, no sin esfuerzo, es de 290 cm/s. Si la cantonera mide 120 cm, y suponiendo despreciable el rozamiento con el aire,

a.- ¿llegará al borde de enfrente o caerá al agua?.

b.- En caso afirmativo habrás terminado, en caso negativo hallar la velocidad que necesita para llegar al borde sin mojarse.

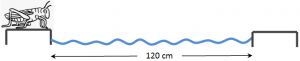
DATO: utilizar el valor de g=9,8 m/s2.

SOLUCIÓN: SI NO QUIERE MOJARSE DEBE LANZARSE CON 3,45 m/s

PREGUNTAS CLÁSICAS AL RESPECTO DEL MOVIMIENTO PARABÓLICO:

MOVIMIENTO PARABÓLICO, CÁLCULO DE LA ALTURA MÁXIMA:

EJERCICIO FQ1BE2307: Desde nuestra posición en clase, lanzamos una goma hacia la papelera, desde una altura de 1,5 m, con una velocidad de 5 m/s que forma un ángulo de 30º con la horizontal. Hallar la altura máxima que alcanza. DATO: g=9,8 m/s2.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/1ibQb5T9xoU

MOVIMIENTO PARABÓLICO, CÁLCULO DEL ALCANCE MÁXIMO:

EJERCICIO FQ1BE2308: Desde el suelo, lanzamos un objeto con una velocidad de 5 m/s que forma un ángulo de 30º con la horizontal. Hallar el alcance máximo. DATO: g=9,8 m/s2.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/NvWpcvHUwv0

MOVIMIENTO PARABÓLICO, OBTENCIÓN DE LA ECUACIÓN DE LA TRAYECTORIA:

EJERCICIO FQ1BE2309: Desde una altura de un metro, lanzamos un objeto con una velocidad de 5 m/s que forma un ángulo de 30º con la horizontal. Hallar la ecuación de la trayectoria. DATO: g=9,8 m/s2.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/9L8jf9HzRUs

MOVIMIENTO PARABÓLICO, CASO PARTICULAR DE LANZAMIENTO (TIRO) HORIZONTAL:

EJERCICIO FQ1BE2310: En el muelle de Agaete, un bañista imprudente, pretende lanzarse al agua sabiendo que tiene que evitar unas rocas que hacen que tenga que alejarse del borde del muelle al menos 3 metros si no quiere quedarse parapléjico por el impacto. El conjunto de rocas se encuentra al nivel del mar, 2 metros por debajo del muelle.

¿Qué velocidad horizontal como mínimo debe comunicarse, si no quiere estar el resto de su vida en silla de ruedas, por la tontería que pretende hacer?

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/XA2Uc-tQ-9c

EJERCICIO FQ1BE2335:

El amarrador es la persona que en el muelle se encarga de asegurar el barco con las cuerdas que se unen fuertemente a los noráis.

La maniobra se inicia lanzando el amarrador desde el muelle una bola unida a una fina cuerda, que a su vez está ligada a la cuerda gruesa con la que se amarra el barco.

El amarrador con pericia lanza a la tripulación del barco esta bola, que una vez la atrapa tira de ella y sube hasta el barco la cuerda definitiva, que se tensa y se procede al amarre seguro del barco.

Como la bola que se lanza está unida a una cuerda, que por su peso y condiciones, no es apropiado considerar que la bola realiza el movimiento como el tiro parabólico habitual (eje horizontal MRU y eje vertical MRUA con la aceleración de la gravedad)

Un amarrador lanza la bola intentando alcanzar al tripulante encima del barco a una altura respecto del amarrador de 4 metros y a una distancia horizontal de 3,5 metros. Se estima que por las características de la cuerda a la que va unida existe una aceleración de frenado adicional de 6 m/s2, tanto en la horizontal como en la vertical.

Si el amarrador lanza la bola con un ángulo de 60º, responder a las siguientes cuestiones: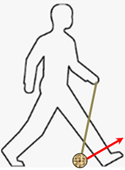

a.- Características del movimiento horizontal y vertical de la bola.

b.- Ecuaciones que describen cada uno de los movimientos.

c.- Obtener la velocidad con la que tiene que lanzar la bola si quiere que llegue al tripulante del barco.

d.- Hallar el vector aceleración en dos puntos intermedios del recorrido de la bola, desde el amarrador hasta el tripulante.

e.- ¿Se puede hablar de movimiento parabólico?

DATO: utilizar el valor de g=9,8 m/s2.

EJERCICIO FQ1BE2336:

Un barquero desea atravesar un río de 45 metros de ancho, utilizando su barca en dirección perpendicular al río. El barquero es capaz de mantener durante toda la travesía una velocidad de 3,5 km/h. La corriente del río es de 2 km/h.

a.- Hallar el tiempo que tarda el barquero en cruzar el río.

b.- Hallar el espacio que ha recorrido la barca, cuando por fin llega a la otra orilla.

c.- Fijando el origen del sistema de referencia la posición inicial del barquero, hallar el vector de posición final (una vez ha llegado a la otra orilla).

d.- Hallar el vector velocidad de la barca cuando t=20s.

e.- Hallar el vector aceleración y su módulo a lo largo de todo el recorrido de la barca.

f.- Hallar la ecuación de la trayectoria del movimiento de la barca.

DATO: g=9,8 m/s2.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/e_UY4JFquEg

EJERCICIO FQ1BE2591:

En el Instituto El Pilar, se ha puesto de moda el juego de la rana, que consiste en lanzar una moneda desde una distancia razonable intentando que entre en la boca de la rana. Por si no ha quedado claro el objetivo se añade el siguiente esquema: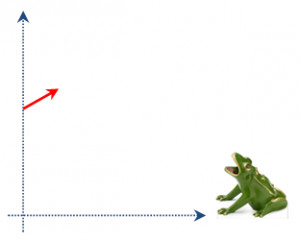

Suponiendo que Pablo va a lanzar desde una distancia de 3,5 metros hasta la boca de la rana, desde una altura de 1,10 metros y con un ángulo de 30º, hallar:

A.- La velocidad que tiene que comunicar Pablo a la moneda para que se la coma la rana, sabiendo que su boca (la de la rana) está a 15 cm del suelo.

B.- Hallar la aceleración del movimiento (vector) en el punto más alto de la trayectoria.

C.- Hallar la velocidad de la moneda (vector) en el punto más alto de la trayectoria

D.- Hallar la ecuación de la trayectoria del movimiento.

E.- Indicar el vector de posición inicial.

F.- Indicar el vector de posición final.

G.- Hallar el vector desplazamiento total.

H. Hallar el vector velocidad final.

DATO: g=9,8 u.S.I.

SOLUCIÓN: vo = 5,22 m/s

EJERCICIO FQ1BE2593:

En el jardín de su casa, Andrea intenta encestar en una medio-canasta de baloncesto que su padre le ha preparado con mucho cariño, amarrando un balde a una altura de 2,5 m, con unas verguillas a la fachada de su casa.

El sustantivo verguilla, que el Diccionario básico de canarismos define como «1. f. Alambre fino. 2. com. Persona muy delgada», procede del también canarismo verga, que a su vez proviene, según explica M. Morera (2001), del portugués verga ‘hilo delgado de metal’ (del latín virga ’vara’). https://www.academiacanarialengua.org/consultas/2020/08/verguilla/

Teniendo en cuenta que Andrea se encuentra a una distancia de 3 metros en horizontal del balde y que el lanzamiento parte de una altura de 1,75 m con un ángulo de lanzamiento de 40o responder a las siguientes preguntas, redondeando a la milésima:

a.- Hacer un dibujo esquema de la situación, indicando claramente el sistema de referencia elegido.

b.- Poner las ecuaciones que van a describir el movimiento de la pelota.

c.- Hallar la velocidad con la que debe lanzar la pelota para encestar en el balde.

d.- Hallar el vector desplazamiento total.

e.- Obtener la ecuación de la trayectoria.

f.- Hallar el vector velocidad final.

DATO: g=9,8 m/s2.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE MOVIMIENTO PARABÓLICO: PRUEBA DE EXAMEN DE FÍSICA Y QUÍMICA 1º BACHILLERATO. MOVIMIENTOS PARABÓLICO Y ARMÓNICO SIMPLE

EJERCICIO FQ1BE2597:

El Roque Nublo se levanta 80 metros sobre su base. Desde la parte más alta del Nublo lanzamos una piedra, con una velocidad del 15 m/s, con un ángulo de 30º. Considerando el origen del sistema de referencia habitual (x=0 e y=80 en el lugar del disparo), responder a las siguientes cuestiones:

a.- Hallar el alcance horizontal máximo contado desde la base del Nublo que alcanza la piedra.

b.- Hallar el vector de posición inicial.

c.- Hallar el vector de posición final.

d.- Hallar el vector velocidad inicial.

e.- Hallar el vector velocidad final.

f.- Hallar el vector aceleración inicial.

g.- Hallar el vector aceleración final.

h.- Hallar el vector desplazamiento total.

i.- Hallar el vector de posición en t=1.

j.- Hallar el vector de posición en t=2.

k.- Hallar el vector desplazamiento entre los instantes t=1 y t=2.

DATO: g=9,8 m/s2.

EJERCICIO FQ1BE2619:

DINÁMICA POLI BUENO-POLI MALO: EL PROFESOR CÓMPLICE

Daniel ha comenzado a entrenar en lanzamiento de jabalina, modalidad olímpica. Se le ha hecho un estudio inicial pormenorizado y se ha llegado a la conclusión de que su velocidad de lanzamiento es de 15 m/s, en su mejor momento.

Se ha constatado igualmente que la jabalina, teniendo en cuenta la altura de Daniel y su particular estilo de lanzamiento, parte de una altura inicial de 1,50 metros sobre el suelo.

En su primer día en el Martín Freire, Daniel realiza un lanzamiento con las características planteadas formando la jabalina un ángulo de 30º con la horizontal.

Para esta situación responder a las siguientes cuestiones, realizando un esquema apropiado de la situación y expresando claramente las ecuaciones del movimiento de la jabalina:

a.- ¿Qué es lo primero que tiene que corregir Daniel con respecto al lanzamiento?

b.- Qué alcance máximo conseguirá Daniel en este primer lanzamiento.

b.1.- Cuánto tiempo está la jabalina en el aire en este caso.

c.- Utilizando el ángulo más apropiado para el lanzamiento, qué alcance hubiera obtenido.

c.1.- ¿Cuánto tiempo estará la jabalina en el aire en este caso.

d.- En algún sitio hemos visto que el record mundial para hombres está en 98,48 m, con lo que suponiendo que ese lanzador utiliza el ángulo apropiado, faltaría más, indicar la velocidad que le comunicó a la jabalina, sabiendo que este lanzador es más alto y la jabalina sale desde una altura de 1,70 m.

e.- Razonar si podemos contar con Daniel en los próximos juegos olímpicos, proponiendo un plan de entrenamiento personalizado, en su caso.

DATO: g=9,8 m/s2.

IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: RESOLUCIÓN PASO A PASO DEL EJERCICIO FQ1BE2619 DE MOVIMIENTO PARABÓLICO

EJERCICIO FQ1BE2620:

DINÁMICA POLI BUENO-POLI MALO: EL PROFESOR CÓMPLICE

Desde el suelo, lanzamos una flecha con una ballesta que sabemos que lleva una velocidad inicial de 40 m/s y que forma un ángulo de 30º con la horizontal. Suponiendo despreciables los rozamientos con el aire durante todo el recorrido:

a.- Realizar un diagrama de la situación, indicando claramente el sistema de referencia elegido.

b.- Expresar las ecuaciones generales y particulares del movimiento objeto de estudio, indicando cada uno de los tipos de movimientos de los que consta.

c.- Obtener el alcance máximo, indicando claramente la condición física que permite obtenerlo.

d.- Obtener la altura máxima, indicando razonadamente y claramente la condición física que permite obtenerla, así como comentarios relativos a la comparación con el apartado anterior.

e.- Obtener el valor de la velocidad con la que impacta la flecha con el suelo, indicando además el ángulo con el que lo hace.

DATO: g=9,8 m/s2.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: RESOLUCIÓN PASO A PASO DEL EJERCICIO FQ1BE2620 DE MOVIMIENTO PARABÓLICO

EJERCICIO FQ1BE2621:

DINÁMICA POLI BUENO-POLI MALO: EL PROFESOR CÓMPLICE

Hallar la ecuación de la trayectoria del ejercicio anterior, FQ1BE2620, representarla en geogebra y contrastar los resultados susceptibles de ello que se obtuvieron en el ejercicio anterior.

EJERCICIO FQ1BE2622:

DINÁMICA POLI BUENO-POLI MALO: EL PROFESOR CÓMPLICE

Un grupo de alumnos pretende cruzar en una barca un río de 25 metros de ancho, remando en dirección perpendicular a la orilla, desde la posición «O», intentando llegar a la orilla opuesta. Se constata que el alumno encargado de remar transmite a la barca en esa dirección perpendicular a la orilla una velocidad de 2 km/h.

La corriente lleva una velocidad de 3 m/s en la dirección indicada en el diagrama. En esta situación y elegiendo el sistema de referencia señalado, se pide: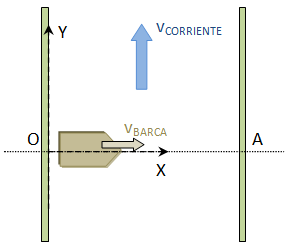

a.- Las ecuaciones del movimiento de la barca en cada uno de los ejes señalados.

b.- El tiempo que tarda la barca en llegar a la orilla opuesta.

c.- ¿Llegará al punto A?. En caso afirmativo argumentar con rigor los motivos y en caso negativo indicar la distancia del punto A a la que llega la barca en la otra orilla.

d.- Utilizando el sistema de referencia indicado, obtener el vector de posición final de la barca así como el módulo de este vector.

e.- Hallar la distancia que ha recorrido la barca.

f.- Obtener la ecuación de la trayectoria de la barca.

g.- Fijándonos en la expresión que determina la ecuación de la trayectoria del apartado anterior, argumentar con rigor si en este caso se puede hablar de movimiento parabólico.

h.- Utilizando geogebra para Ipad, representar la ecuación de la trayectoria de la barca obtenida en el apartado f y la recta x=25. Contrastar con esta representación todo lo que podamos de lo obtenido en el desarrollo del ejercicio.

DATO: g=9,8 m/s2.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: RESOLUCIÓN PASO A PASO DEL EJERCICIO FQ1BE2622 DE MOVIMIENTO PARABÓLICO

EJERCICIO FQ1BE2623: EJERCICIO DE RECOPILACIÓN DE DESTREZAS BÁSICAS AL RESPECTO DEL MOVIMIENTO PARABÓLICO

Con una ballesta último modelo, dotado de los mejores avances al respecto y con una flecha extremadamente aerodinámica, realizamos un lanzamiento desde una altura de dos metros, que forma un ángulo de 30º con la horizontal. El fabricante del equipo nos indica que la flecha sale con una velocidad de 100 m/s. Para esta realidad, responder a las siguientes preguntas:

a.- Realizar el esquema/dibujo/diagrama de la situación, donde se observe claramente el Sistema de Referencia elegido.

b.- Indicar las ecuaciones generales del movimiento señalando los tipos de movimiento que se producen en cada uno de los ejes del S.R.

c.- Indicar las ecuaciones particulares del movimiento de esta flecha.

ALERTA MÁXIMA: todo lo que vendrá a continuación se obtendrá de estas ecuaciones de partida.

d.- Obtener el alcance máximo de la flecha, indicando la condición física que nos permite obtenerlo.

e.- ¿Cuánto tiempo está la flecha en el aire?

f.- Hallar la altura máxima que alcanza la flecha, indicando la condición física que nos permite obtenerla.

g.- Indicar la distancia horizontal medida desde el momento del disparo a la que se alcanza la altura máxima del apartado anterior.

h.- Obtener la ecuación de la trayectoria del movimiento, haciendo comentarios al tipo de movimiento que describe.

i.- Indicar el vector aceleración en el punto más alto de la trayectoria y a los dos segundos de iniciado el movimiento de la flecha.

j.- Indicar el vector de posición inicial y su módulo..

k.- Indicar el vector de posición final y su módulo..

l.- Indicar el vector velocidad inicial y su módulo.

m.- Indicar el vector velocidad final y su módulo..

n.- Hallar el ángulo que forma la flecha con la vertical, cuando al final de su movimiento se clava en el suelo.

ñ.- Indicar el vector velocidad en el punto más alto de la trayectoria y su módulo.

o.- Hallar el vector desplazamiento total y su módulo.

DATO: g=9,8 m/s2.

SOLUCIONES: d) 886,784 m; e) 10,24 s; f) 129,55 m; g) y=2+0,58x-0,000653x2

 

APORTAMOS MATERIAL ADICIONAL A ESTE CONTENIDO, EN EL DOCUMENTO QUE SE AÑADE A CONTINUACIÓN:

Añadimos un acercamiento al bilingüismo, para que nuestros alumnos vean que con esto de las asignaturas de ciencias, incluso con un nivel básico de Inglés, es posible interpretar algunos enunciados, como preparación a lo que está por venir en la Universidad, consultando textos extranjeros.

42 CINEMATICA DE MRU A PARABOLICO V19

ASPECTOS FORMALES DE LA ACTIVIDAD:

SE PRETENDE PARA BACHILLERATO, CON ESTA DINÁMICA, EL DESARROLLO DE LAS COMPETENCIAS CLAVE:

CON RESPECTO A LOS SABERES BÁSICOS DE FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO:

CON RESPECTO A LAS COMPETENCIAS ESPECÍFICAS DE FÍSICA Y QUÍMICA DE 1º DE BACHILLERATO QUE SE CONSIDERAN:

FYQ 1BAC C1 , FYQ 1BAC C2 , FYQ 1BAC C3 , FYQ 1BAC C4 , FYQ 1BAC C5 , FYQ 1BAC C6

VINCULADOS A LOS DESCRIPTORES OPERATIVOS  de las Competencias Clave CORRESPONDIENTES

CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN, VINCULADOS A LAS CORRESPONDIENTES COMPETENCIAS ESPECÍFICAS:

FYQ1BAC1.1 , FYQ1BAC1.2 , FYQ1BAC2.3 , FYQ1BAC3.1 , FYQ1BAC3.3 , FYQ1BAC6.1 

Incluyen los descriptores operativos asociados

SE CONTEMPLAN LOS ASPECTOS RELACIONADOS CON EL PERFIL DE SALIDA DEL ALUMNADO DE LOS INSTITUTOS DIOCESANOS DE CANARIAS

PODRÍA INTERESAR LA VISITA AL SIGUIENTE ARTÍCULO DEL PROYECTO, DONDE SE DESARROLLAN LAS ASIGNATURAS DE FÍSICA Y QUÍMICA DE SECUNDARIA Y BACHILLERATO:

Post Views: 7.036
On:

Comments are closed, but trackbacks and pingbacks are open.