MOVIMIENTO CIRCULAR UNIFORME FÍSICA

MOVIMIENTO CIRCULAR UNIFORME:MOVIMIENTO CIRCULAR UNIFORME FÍSICA

CRITERIO DE EVALUACIÓN 8 DE FYQ DE 4º DE LA E.S.O. Y CRITERIO 7 DE FYQ DE 1º BACHILLERATO

Entre otras cosas, el movimiento circular uniforme es la antesala del movimiento planetario, de las Leyes de Kepler, de ahí su importancia y el motivo de que nos ocupemos de él.

Dentro del proyecto, se incluye en el contenido amplio DE CIRCULAR A KEPLER, que debe ser consultado para un mejor acercamiento a este movimiento, en el apartado correspondiente, aunque aquí sólo nos ocuparemos de los aspectos más prácticos del movimiento circular uniforme.

ASPECTOS FORMALES PARA DOCENTES, AL FINAL DEL ARTÍCULO:

Debemos empezar en clase, preguntando a los alumnos, cuestiones como las siguientes:

  • ¿Qué movimientos circulares conoces?
  • ¿Alguno realmente importante?
  • …

LA SIGUIENTE IMAGEN PODRÍA SER UNA BUENA «CHULETA-RESUMEN» QUE DESCRIBE EL MOVIMIENTO CIRCULAR UNIFORME Y MUESTRA LAS RELACIONES ENTRE LAS MAGNITUDES IMPLICADAS EN EL MISMO:

MOVIMIENTO CIRCULAR UNIFORME FÍSICA

Para introducirnos en este movimiento circular, puede ser de interés el visionado del siguiente material audiovisual de aspectos teóricos: https://youtu.be/Sc4vRp2YQa8

ORIENTACIONES PARA UNA POSIBLE ADAPTACIÓN, CUANDO SEA NECESARIO, POR DIFERENTES MOTIVOS:

DESCRIPCIÓN CUALITATIVA DEL FENÓMENO OBSERVADO:

  • Cuando gira un tiovivo, ¿todos los caballitos van a la misma velocidad?.
  • La típica velocidad, la de m/s o km/h ¿es la única velocidad que existe en el movimiento circular uniforme?
  • Intentar definir lo que es un ángulo
  • En el sistema habitual (sexagesimal) y en el sistema de radianes, indicar el valor de un ángulo recto y de la circunferencia completa.
  • ¿por qué nos fastidian con la nueva medida de ángulos en radianes?
  • Definir claramente velocidad lineal y velocidad angular.
  • ¿En qué casos es necesario utilizar la velocidad angular?
  • Qué significa M.C.U.
  • Describir las características de los M.C.U.
  • ¿Cuál es la unidad del ángulo en el S.I.?
  • ¿Cuál es la unidad de la velocidad angular en el S.I.?
  • La Tierra alrededor del Sol, ¿se mueve con un M.C.U.?
  • La velocidad, la posición ¿de qué variables depende?
  • Definir con rigor términos relacionados: movimiento, rectilíneo, uniformemente, acelerado, velocidad, velocidad angular, aceleración, aceleración tangencial, aceleración normal, posición, Sistema de Referencia, variables, constantes, circular, frecuencia, período, radio.
  • ¿Un M.C.U. tiene aceleración?
  • ¿Cuál es la causa del movimiento de la Tierra alrededor del Sol?
  • Aspectos mencionados en el material audiovisual: https://youtu.be/Sc4vRp2YQa8
  • Descripción del movimiento, ecuaciones características y relaciones entre las magnitudes implicadas que se muestran en la CHULETA RESUMEN.

OTRAS CUESTIONES RELACIONADAS CON LA OBSERVACIÓN CUALITATIVA DEL M.C.U.:

1.- Responder si son ciertas o no las siguientes afirmaciones:

a) Se define la aceleración como la variación del módulo de la velocidad con respecto al tiempo.
b) Se define la aceleración como la variación de la dirección de la velocidad con respecto al tiempo.
c) Ambas son ciertas.

2.- Para calcular el ángulo que describe un cuerpo con M.C.U., cuando se conoce el radio, no hay más que:

a) multiplicar el espacio recorrido por el radio.
b) dividir el espacio recorrido por el radio.
c) igualar el espacio recorrido al radio.

3.- ¿Se puede relacionar la velocidad angular con la velocidad lineal? ¿Qué fórmula las relaciona?

4.- Razona la respuesta: el MCU es acelerado:

a) Porque cambia el tamaño del radio durante la trayectoria.
b) Porque cambia el tamaño del vector velocidad.
c) Porque cambia la dirección del vector velocidad.
d) Sólo cuando no va siempre igual de rápido.

5.- Hay dos puntos sobre un disco que gira, uno ubicado en el borde exterior y el otro ubicado muy cerca al centro. Cuál de los dos puntos recorre mayor distancia en una vuelta completa? ¿Cuál de los dos puntos tiene una mayor velocidad lineal? ¿Cómo es la velocidad angular de un cuerpo respecto a la que lleva el otro?

6.- Define período y frecuencia, ¿qué relación hay entre ambas magnitudes?

7.- ¿Cuál es el período de rotación de La Tierra y cuál el de traslación?

8.- ¿Cómo se representa el vector velocidad cuando la trayectoria es circular?

REPRESENTACIÓN DE LA SITUACIÓN QUE SE EXPONE EN EL EJERCICIO/ACTIVIDAD:

Realizar un dibujo-esquema de la situación que se describe en el enunciado textual, tomando nota de los datos o información que aporta el enunciado en lugar correspondiente, así como dibujo de la trayectoria que se describirá.

USO BÁSICO DE LAS ECUACIONES CARACTERÍSTICAS DEL MOVIMIENTO:

En las ecuaciones características identificar cada uno de los elementos presentes, según se comente en el enunciado de cada ejercicio, asignándoles el valor numérico que corresponda, si se suministra en el enunciado textual. Incluir el signo correcto en función del sistema de referencia utilizado; así como identificar el elemento o magnitud que nos piden que calculemos.

Los cálculos asociados a la ecuación, despejar la magnitud correspondiente, corresponde al siguiente paso, en donde se ponen de manifiesto las estrategias matemáticas del ejercicio.

Las cuestiones más sencillas desde el punto de vista matemático, que se plantean desde este proyecto ACHIMAGEC, las hemos identificado como de NIVEL 1.

EJERCICIO FQ4EE2317, (NIVEL PRO para 4º E.S.O.):

En un futuro no muy lejano, la Federación Internacional de Observación de la Tierra y Marte desde Fuera (F.I.O.T.M.F.) ha puesto en marcha la iniciativa de colocar justo en medio de la Tierra y de Marte una estación que orbite alrededor del Sol, con la que poder observar tanto la Tierra como Marte.

La 3ª Ley de Kepler nos indica una relación entre la órbita de la estación y el tiempo que tarda en realizar una vuelta completa, al igual que con la Tierra y con Marte.

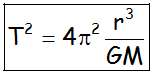
      • Donde T es el tiempo que tarda en dar una vuelta completa a la órbita, en unidades del S.I..
      • M es la masa del Sol en este caso, ya que es la masa del creador del campo gravitatorio causante del movimiento orbital.
      • r es el radio de la órbita.
      • G es la Constante de Gravitación Universal.

a.- ¿A qué distancia del Sol estará la órbita de la estación?

b.- ¿Cuántos días tardará la estación en dar una vuelta completa al Sol?

c.- Utilizando la 3ª Ley de Kepler y los datos suministrados de la Tierra, obtener el número de días que tarda la Tierra en completar una órbita completa. Confirmar o no la coincidencia con el año terrestre.

d.- Obtener la velocidad lineal de la Tierra a lo largo de su órbita.

e.- Utilizando la 3ª Ley de Kepler y los datos suministrados de Marte, obtener el número de días que tarda Marte en completar una órbita completa. Comparar con el año terrestre.

DATOS: Rórbita de la Tierra=150·109 m; Rórbita de Marte=227,9·109 m; MSol=1,989·1030 kg; G=6,67·10-11 N·m2/kg2.

PROPUESTA DE EJERCICIOS:

EJERCICIO F4EE2169:

Omar y Alberto van montados en dos caballitos que giran con el tiovivo que los contiene a 5 vueltas por minuto. El caballo de Omar está a una distancia de 3 metros del eje de giro del tiovivo y el de Alberto a una distancia de 4 metros.

a.- ¿Quién se mueve más rápido? O lo que es lo mismo ¿Cuál de los dos protagonistas se despeina más?.

b.- Hallar la velocidad angular en unidades del S.I.

c.- Hallar el número de vueltas que da cada uno en 10 minutos.

d.- Hallar la frecuencia del movimiento circular.

e.- Hallar el periodo del movimiento circular.

f.- Hallar la aceleración de cada uno de ellos.

g.- Hallar el espacio que recorre cada uno de ellos en 3 minutos.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/gXVpW3V9J2Y

h.- Si posteriormente José Luis se sube al tiovivo, colocándose a una distancia de 4,5 metros del eje de giro, manteniendo Omar y Alberto sus posiciones iniciales. ¿Cuál de ellos se despeina más?.

EJERCICIO FQ4EE2171:

Un biciclo como el que se muestra, antecesor de las bicicletas actuales, se mueve (no sin dificultad) con una velocidad de 54 km/h.

El radio de la rueda delantera es de 75 cm y el radio de la rueda trasera tan solo de 20 cm. En esta situación se pide:

a.- La velocidad lineal de un punto de la periferia de cada una de las ruedas en el Sistema Internacional de unidades.

b.- La velocidad angular de cada una de las ruedas en el Sistema Internacional de unidades.

c.- El periodo de cada una de las ruedas.

d.- La frecuencia de cada una de las ruedas.

e.- El espacio que recorre la bicicleta en media hora.

f.- El ángulo que describe cada una de las ruedas en 1 segundo.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/sx5XxPMCyJU

EJERCICIO F4EE2170:

En el lejano Oeste, un carromato que se utiliza para el transporte de mercancías en Arizona, realiza el trayecto habitual. El carromato dispone de cuatro ruedas: las dos delanteras de 75 cm de radio cada una y las dos traseras, de 85 cm de radio cada una. En el instante que nos ocupa, el carromato va a una velocidad de 36 km/h. En esta situación se nos pide:

a.- Sin realizar ningún cálculo previo, razonar cuál de los dos tipos de ruedas gira a mayor velocidad, es decir, cuál de los dos ejes (el delantero o el trasero) necesitará antes una reparación por parte del herrero del pueblo más cercano.

b.- Obtener el valor de la velocidad angular de cada uno de los dos tipos de ruedas en unidades del S.I. y en r.p.m.

c.- Obtener el periodo del movimiento circular de las ruedas delanteras.

d.- Obtener la frecuencia del movimiento circular de las ruedas traseras.

e.- Kill Bill, el pistolero más rápido de la zona, en un disparo poco acertado, dejó alojada una bala en la rueda delantera izquierda, a 15 cm del eje de giro. Hallar la velocidad lineal de la bala.

f.- Hallar la velocidad lineal de un punto de la periferia de las ruedas delanteras.

g.- Hallar la velocidad lineal de un punto de la periferia de las ruedas traseras.

h.- Hallar el número de vueltas que da cada una de las ruedas en 2 minutos.

EJERCICIO FQ4EE2172 (NIVEL 1):

En un parque de atracciones, una plataforma circular de 10 m de radio se encuentra girando, en un momento determinado, en torno a su eje, a 6 revoluciones por minuto (r.p.m.). Mientras se mantiene este movimiento circular uniforme:

a.- Hallar la velocidad angular de la plataforma en unidades del S.I.

b.- Hallar la velocidad lineal de un punto de la periferia de la plataforma.

c.- Hallar el espacio que recorre un usuario que se encuentra sentado a 3 metros del borde de la plataforma en los 15 segundos que dura el movimiento circular uniforme.

d.- Hallar el Periodo y la frecuencia del movimiento mientras se mantienen constantes las 6 revoluciones por minuto.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/NoZYb6SFqAo

EJERCICIO FQ1BE2174:

Una patineta eléctrica se mueve a una velocidad reglamentaria de 18 km/h por un carril bici. La rueda delantera tiene un diámetro de 30 cm y la trasera 20 cm de radio.

a.- Hallar la velocidad lineal de un punto de la periferia de cada una de las ruedas en unidades del Sistema Internacional.

b.- Hallar la velocidad angular de cada una de las ruedas en unidades del S.I. y en revoluciones por minuto.

c.- Indicar el periodo y la frecuencia de la rueda trasera.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/rIU9eYzytwg

EJERCICIO FQ4EE2333:

Nuestro planeta Tierra, se puede considerar, sin que ello sea una aproximación muy disparatada, que realiza un movimiento circular uniforme alrededor del Sol, la traslación. Sabiendo que la Tierra se encuentra a 150 millones de km del Sol (corresponde a una U.A. unidad astronómica), hallar la velocidad de nuestro planeta en su viaje de traslación alrededor del Sol. Hay que tener en cuenta el tiempo que dura una traslación.

Hacerlo en primer lugar en km/h (para caer en la cuenta de la magnitud de esa velocidad) y pasarlo posteriormente a Unidades del S.I.

Deberíamos sorprendernos del resultado, en el sentido de que llevamos 4,6 miles de millones de años realizando este viaje a enorme velocidad. Realmente para flipar.

Buscando en la red, se dice que la sonda espacial Juno alcanzó cerca de Júpiter la velocidad de 265540 km/h.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/vSmvc85DcMs

EJERCICIO FQ4EE2334:

Nuestro planeta Tierra, gira sobre sí mismo en torno a un eje que pasa por los Polos en su movimiento de rotación. Teniendo en cuenta que el radio de la Tierra es de 6371 km. Hallar la velocidad de alguien que se encuentre en algún punto del Ecuador de la Tierra, como consecuencia de su rotación. Hay que tener en cuenta el tiempo que dura una rotación del planeta.

Hacerlo en primer lugar en km/h (para caer en la cuenta de la magnitud de esa velocidad) y pasarlo posteriormente a Unidades del S.I.

Deberíamos reconocer que tampoco es ninguna broma esta velocidad. Con los resultados obtenidos en este ejercicio y en el anterior, me cuesta trabajo pensar que ni nos mareemos, ni nos despeinemos, teniendo en cuenta que estamos subidos en una especie de vagoneta que viaja a toda pastilla por el Universo, en el efecto combinado de la traslación y la rotación.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/xKhK5XrawH4

EJERCICIO FQ4EE2337:

Un planeta (XP78B) gira alrededor de su estrella a una distancia de 3,7 u.a. y tarda 2,2 años terrestres en dar una traslación completa. Hallar la velocidad angular y lineal del planeta. En km/h y en unidades del S.I.

EJERCICIO FQ4EE2338:

La estación espacial internacional (I.S.S.) está a 354 km sobre la superficie de la Tierra, completando su traslación alrededor de la Tierra en 90 minutos.

Si el radio de la tierra es de 6371 km, hallar:

a.- La velocidad lineal de la estación en km/h y unidades del S.I.

b.- La velocidad angular de la ISS, en unidades del S.I.

c.- El número de vueltas que da la ISS en un día.

EJERCICIO FQ4EE2351:

La bicicleta de Juan tiene ruedines. Las ruedas tienen un radio de 35 cm y los ruedines un diámetro de 25 cm.

Juan va a 15 km/h.

a.- Hallar la velocidad lineal de un punto de la periferia de las ruedas en unidades del S.I.

b.- Hallar la velocidad angular de la rueda.

c.- Hallar la velocidad angular de los ruedines.

d.- Juan, que se preocupa mucho por la seguridad, tiene un captadiótricos de Hello Kitty a una distancia de 15 cm del centro de la rueda. Hallar la velocidad lineal de Hello Kitty.

e.- Hallar la velocidad angular de H-K en r.p.m.

f.- Hallar el periodo de los ruedines.

g.- Hallar el periodo de las ruedas

h.- Hallar la frecuencia de los ruedines.

EJERCICIO FQ4EE2363:

Pablo, entrenando al fútbol, en una entrada desafortunada, se rompe el menisco, con lo que tiene que utilizar una silla de ruedas. La rueda trasera, tiene un diámetro de 80 cm, y la delantera tiene un radio de 10 cm.

En un momento en que Pablo, haciendo el loco, va a una velocidad de 5 km/h, hallar:SILLA DE RUEDAS

a.- la velocidad lineal, en unidades del S.I., de un punto de la periferia, de la rueda delantera.

b.- la velocidad lineal, en unidades del S.I., de un punto de la periferia,  de la rueda trasera.

c.- La velocidad angular, en r.p.m. de la rueda delantera.

d.- La velocidad angular, en rad/s de la rueda trasera.

e.- El periodo de la rueda delantera.

f.- El periodo de la rueda trasera.

g.- El tiempo que tarda Pablo en recorrer un kilómetro.

h.- ¿Cuál de las dos ruedas tiene mayor frecuencia?

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/VweG5Eobq-s

OTROS EJERCICIOS:

1.- La noria de un parque de atracciones tarda 15 s en dar una vuelta. Si su velocidad angular es constante, calcula:

  1. Velocidad angular en rad/s
  2. El período y la frecuencia
  3. El ángulo girado en 5 s.
  4. La velocidad lineal de un viajero situado a 10 m del eje de giro.

Soluciones:  0’41 rad/s; 15 s; 0’06 Hz; 2’04 rad ; 4’1 m/s

2.- La velocidad angular de un tocadiscos de 1970 es de 45 r.p.m. Calcula:

  1. Velocidad angular en rad/s
  2. Número de vueltas que dará en 5 minutos.
  3. Espacio lineal recorrido por una mosca situada sobre el disco a 10 cm del centro en ese tiempo.

Soluciones:  4’71 rad/s; 225 vueltas; 141’37 m

3.- Si un cuerpo gira con una velocidad angular de 15 rad/s en un círculo de 1’5 m de radio, averigua:

  1. Número de vueltas que da en 10 s
  2. Espacio lineal recorrido en ese tiempo.
  3. Período y frecuencia del movimiento.

SOLUCIONES: 23,87 vueltas; 225 m; 2,38 Hz

4.- Uno de los caballos de un tiovivo, situado a 1 m del centro del mismo, gira a razón de 3 vueltas por minuto. Calcula:

  1. Velocidad angular en rad/s
  2. Velocidad lineal del caballo.
  3. Aceleración normal de dicho caballo.

SOLUCIONES: 0,31 rad/s; 0,31 m/s; 0,1 m/s2.

5.- Un punto describe una trayectoria circular de 30 cm de radio tardando 3,52 s en dar cinco vueltas. Calcular:

  1. La velocidad angular en r.p.m y en rad/s
  2. El periodo y la frecuencia del movimiento
  3. El ángulo girado al cabo de 0,85 s de iniciado el movimiento.
  4. Su aceleración centrípeta

SOLUCIONES: 85,23 r.p.m.; 2,84 π rad/s; 0,704 s; 1,42 Hz; 7,58 rad; 23,88 m/s2.

6.- Un punto recorre una trayectoria circular de radio 36 cm con una frecuencia de 0,25 s-1.

  1. Calcular el periodo del movimiento.
  2. Calcular la velocidad angular y la lineal.
  3. Determinar el ángulo girado en 1,54 s.
  4. La aceleración normal o centrípeta.

EJERCICIO QUE INCORPORA LA DINÁMICA DEL MOVIMIENTO CIRCULAR:

EJERCICIO FQ4EE2395:

La velocidad máxima con la que un vehículo de 1300 kg de masa puede coger una curva de 180 m de radio es de 60 km/h. Hallar:

a.- La fuerza de rozamiento existente.

b.- El coeficiente de rozamiento entre las ruedas y el asfalto.

DATO: g=9,8 m/s2

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/OT9tKLaRlH8

ASPECTOS FORMALES PARA DOCENTES:

SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS:

SE TRABAJAN ADEMÁS DE LOS ASPECTOS PROPIOS DEL CONTENIDO, LA NOMENCLATURA CIENTÍFICA Y EL CAMBIO DE UNIDADES UTILIZANDO FACTORES DE CONVERSIÓN.

PODRÍA INTERESAR LA VISITA AL SIGUIENTE ARTÍCULO DEL PROYECTO, DONDE SE DESARROLLAN LAS ASIGNATURAS DE FÍSICA Y QUÍMICA DE SECUNDARIA Y BACHILLERATO:

Post Views: 6.420
On:

Comments are closed, but trackbacks and pingbacks are open.