RESOLUCIÓN PASO A PASO DEL EJERCICIO FQ1BE2549 DE MOVIMIENTO ARMÓNICO SIMPLE

EJERCICIO RESUELTO MOVIMIENTO ARMÓNICO

EJERCICIO FQ1BE2549, TAREA INTERDEPARTAMENTAL MAT/FYQ:

Sabemos que en un oscilador armónico, cuerpo que se mueve con un movimiento armónico simple, en ausencia de rozamientos, se conserva la energía mecánica, que es igual a la suma de la energía cinética y la energía potencial:

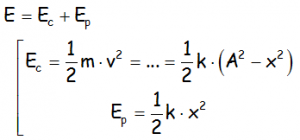
Para un movimiento armónico, cuyas expresiones de la energía cinética y la potencial en función de la posición responde a: E_c(x) = 10 – 2,5 x² ; E_p(x) = 2,5 x² . Para una partícula de 25 g de masa que vibra según se indica, responder a las siguientes cuestiones:

a.- Identificar la amplitud del movimiento.

b.- Localizar analíticamente los puntos de corte con los ejes de cada una de las funciones, indicando el sentido físico de cada uno de estos puntos.

b.1.- Hallar la velocidad máxima que alcanza el oscilador.

c.- Encontrar la ecuación/expresión de la función que nos indicaría la energía mecánica del oscilador armónico, E(x).

c.1.- Indicar el máximo valor de la energía cinética y el máximo valor de la energía potencial, comparándolo con el valor de la energía mecánica obtenido en el apartado anterior.

d.- Localizar el punto o puntos, indicando la posición y la energía correspondiente, en el que la energía cinética es igual que la potencial, obteniéndolos analíticamente.

e.- Obtener para la ecuación que responde a la energía cinética la posición de su punto crítico, confirmando analíticamente y a través de la primera y segunda derivada si es máximo o mínimo, así como la curvatura. Para este punto indicar además el sentido físico del mismo.

f.- Confirmar para la ecuación que responde a la energía potencial la posición de su punto crítico, confirmando analíticamente y a través de la primera y segunda derivada si es máximo o mínimo, así como la curvatura. Para este punto indicar además el sentido físico del mismo.

g.- Representar las tres funciones Ec(x), Ep(x) y E(x), con toda la información obtenida en los apartados anteriores.

h.- A través de geogebra, representar las tres funciones: Ec(x), Ep(x) y E(x), prestando atención al dominio de las funciones.

UTILIZACIÓN DE GEOGEBRA EN MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO.

i.- Indicar el valor de la constante k del oscilador armónico.

j.- Si la partícula que vibra tiene una masa de 25 g, indicar el valor del periodo de oscilación.

j.1.- Hallar el valor de la frecuencia angular (w).

k.- Teniendo en cuenta el valor de la masa del apartado anterior, obtener la ecuación de la posición, de la velocidad y de la aceleración en función del tiempo, sabiendo que en el instante inicial la partícula se encuentra en x=0 m. Representarlas en geogebra, intentando extraer conclusiones de las gráficas cinemáticas combinadas.

k.1.- Con la expresión de la velocidad, confirmar la velocidad máxima obtenida en el apartado b.1.

l.- Realizar el apartado anterior considerando que la partícula en el instante inicial se encuentra en la posición x=2 m.

PUEDE INTERESAR LA CONSULTA DEL ARTÍCULO: TRIGONOMETRÍA: ECUACIONES TRIGONOMÉTRICAS

m.- Realizar el apartado anterior considerando que la partícula en el instante inicial se encuentra en la posición x=-2 m.

SOLUCIÓN PASO A PASO DEL EJERCICIO:

EJERCICIO FQ1BE2549 MOVIMIENTO ARMÓNICO ANÁLISIS FUNCIONES