EXAMEN ANÁLISIS MATEMÁTICAS II
BLOQUE DE ANÁLISIS DE FUNCIONES
PRUEBA DE EXAMEN DE MATEMÁTICAS II, PARA 2º DE BACHILLERATO (X655), DEL BLOQUE DE ANÁLISIS DE FUNCIONES,
REALIZADA EN «EL PILAR»:
PUEDE INTERESAR LA CONSULTA DE:
ESTA PRUEBA SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA:
LOS EJERCICIOS DE LA PRUEBA Y SUS SOLUCIONES PASO A PASO
EJERCICIO M2BE2275 (M2BE2161):
Calcula los parámetros a y b para que la función definida a continuación sea derivable en todo ℜ.
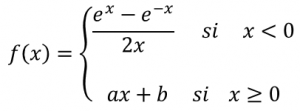
LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO:
EJERCICIO M2BE2276 A:
Calcular el siguiente límite:
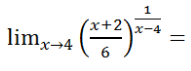
LA SOLUCIÓN, UTILIZANDO LA FÓRMULA:
LA SOLUCIÓN, PASO A PASO, LLEVANDO LA EXPRESIÓN AL LÍMITE QUE SE CORRESPONDE CON EL NÚMERO e, QUE DEBE SER CONSIDERADA UNA CONFIRMACIÓN DE LA RESOLUCIÓN ANTERIOR:
EJERCICIO M2BE2276 B:
Calcular el siguiente límite:
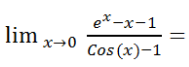
LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE LÍMITES:
EJERCICIO M2BE2277:
Dada la siguiente función f(x):
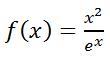
a.- Determinar los intervalos de crecimiento y los de decrecimiento.
b.- Calcular los máximos y mínimos relativos.
LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE MONOTONÍA Y MÁXIMOS Y MÍNIMOS:
EJERCICIO M2BE2278:
Un agricultor llamado OMAR, se compró un terreno rústico en Santa Brígida. El terreno, está limitado por las funciones:
f(x) = x2 – 4x + 4 y g(x) = – x2 + 4
Suponemos que el gráfico está en metros.
a.- Realiza un gráfico del terreno que adquirió Omar.
b.- Calcula el precio del terreno, si cada metro cuadrado en Santa Brígida tiene un valor aproximado de 18500 euros. Alberto dice que costó menos de 48000 euros ¿está en lo cierto?.
LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: