ESTUDIO DERIVABILIDAD FUNCIONES BACHILLERATO

ESTUDIO DE LA DERIVABILIDAD DE UNA FUNCIÓN:

¡Los ingenieros tienen que construir carreteras contínuas y derivables!

Una función es contínua cuando la dibujamos sin levantar el lápiz del papel.

Una función es derivable cuando no presenta cambios bruscos en la dirección, cuando no presenta puntos angulosos.

Está claro por qué las carreteras deben ser contínuas y derivables, señores ingenieros.

ASPECTOS FORMALES PARA DOCENTES, ACTUALIZADOS LOMLOE, AL FINAL DEL ARTÍCULO, PARA NO INTERFERIR CON LO QUE TIENE INTERÉS PARA EL APRENDIZAJE DE LOS ALUMNOS

PARA ESTUDIAR LA CONTINUIDAD DE UNA FUNCIÓN SE APLICA LA DEFINICIÓN DE CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO, que en funciones «artificiales-fabricadas» a trozos, normalmente consiste en tener en cuenta que los límites laterales coinciden.

Una función f(x) es contínua en un punto x=x₀ si:

Lo anterior significa que debe existir el valor de la función en ese punto y coincidir con el límite en él (para lo cual a su vez deben coincidir los límites laterales). Esto es muy necesario estudiarlo cuando tenemos funciones a trozos.

PARA ESTUDIAR LA DERIVABILIDAD DE UNA FUNCIÓN EN UN PUNTO (QUE TIENE QUE SER PREVIAMENTE CONTÍNUA), SE APLICA LA DEFINICIÓN DE CONTINUIDAD DE UNA FUNCIÓN EN UN PUNTO A LA FUNCIÓN DERIVADA, que en funciones a trozos, normalmente consiste en que las derivadas laterales (los límites laterales de la derivada) coincidan.

SE RECOMIENDA EN LOS EJERCICIOS, REPRESENTAR LA FUNCIÓN OBTENIDA Y COMPROBAR QUE LAS RAMAS EN CONFLICTO «ENLAZAN» Y QUE LO HACEN «SIN CAMBIOS BRUSCOS EN LA DIRECCIÓN» DE ENLACE.

EJERCICIO M2BE1992 JL:

Dada f(x), hallar los valores de m para que la función sea derivable en todo ℜ:

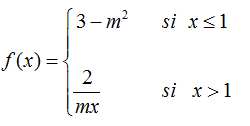
IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/YxFgioPnfdg

EJERCICIO M2BE2017:

Dada la función:

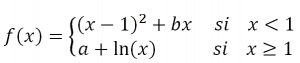
a.- Estudia los valores de los parámetros a y b para que la función f(x) sea continua y derivable en ℜ. Escribe la función resultante f(x).

b.- Tomando los valores a=-2 y b=1, calcula la ecuación de la recta tangente en x=e.

VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/foUIAm2GnC4

EJERCICIO M2BE2316 (M2BE1992 AMPLIADO):

a.- Dada f(x), hallar los valores de m para que la función sea derivable en todo ℜ:

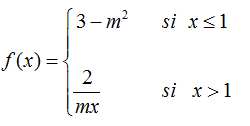
b.- Si m = 2, calcular la recta tangente a f(x) en x=3

IR A LA SOLUCIÓN DEL EJERCICIO

EJERCICIO M2BE2602:

Calcula los parámetros a y b para que la función definida a continuación sea derivable en todo ℜ.

IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTE EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS II DE 2º DE BACHILLERATO. ANÁLISIS DE FUNCIONES PRIMER TRIMESTRE 2024-25

EJERCICIO M2BE1993:

Estudiar la derivabilidad de la función f(x):

Representarla y justificar los resultados analíticos con la representación gráfica, realizando los comentarios pertinentes.

EJERCICIO M2BE1994:

Hallar a y b para que la siguiente función sea derivable en todo el dominio:

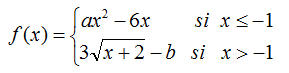
EJERCICIO M2BE2161:

Calcula los parámetros a y b para que la función definida a continuación sea derivable en todo ℜ.

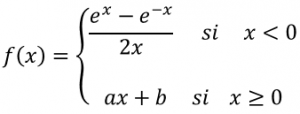
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN GEOMETRÍA, ÁLGEBRA, ANÁLISIS PARA MATEMÁTICAS 2º BACHILLERATO

LA RESOLUCIÓN DE OTRA FORMA: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24

EJERCICIO M2BE1995 (EBAU CANARIAS 2021):

Dada la función:

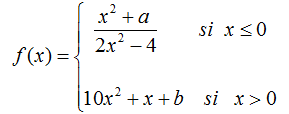
Calcular los valores de los parámetros a y b para que la función sea contínua y derivable en ℜ.

Dar las expresiones de la función f(x) y de su derivada f´(x)

EJERCICIO M2BE1996 (EBAU CANARIAS 2019):

Dada la siguiente expresión, de la función f de la que se desconocen algunos valores:

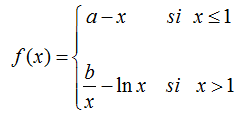
Calcular los valores de a y b para que sea derivable en todo su dominio.

Escribir la función resultante.

EJERCICIO M1BE1997:

Estudiar la continuidad y derivabilidad de la siguiente función, que debe ser expresada como una función a trozos:

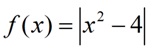
Representar la función y contrastar lo obtenido analíticamente con la representación gráfica, haciendo los comentarios necesarios.

RECOMENDABLE: Realizar la representación en geogebra.

EJERCICIO M1BE1998:

Estudiar la continuidad y derivabilidad de las siguientes funciones.

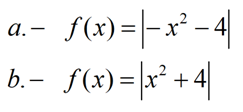
EJERCICIO M1BE2002:

Realizar el estudio completo de la función f(x) siguiente. Se recomienda convertirla previamente en la función a trozos correspondiente:

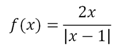
CONCLUSIONES SOBRE EL VALOR ABSOLUTO:

El valor absoluto tiene un comportamiento especial, ya que sólo actúa cuando le interesa… si lo de dentro es positivo, no hace nada, lo deja pasar… si lo de dentro es negativo, no le gusta, y le cambia el signo.

Para reflexionar, con respecto a la inmovilidad del valor absoluto cuando lo de dentro es positivo:

«Cuando los nazis vinieron a llevarse a los comunistas, guardé silencio, ya que no era comunista.
Cuando encarcelaron a los socialdemócratas, guardé silencio, ya que no era socialdemócrata.
Cuando vinieron a buscar a los sindicalistas, no protesté, ya que no era sindicalista.
Cuando vinieron a llevarse a los judíos, no protesté, ya que no era judío. Cuando vinieron a buscarme, no había nadie más que pudiera protestar».

Martin Niemöller (1892-1984).

EJERCICIO M2BE2177:

Para la función f(x) definida del siguiente modo:

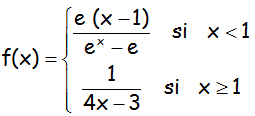
a.- Estudiar su derivabilidad.

IR AL ARTÍCULO CON LA SOLUCIÓN DE ESTE EJERCICIO DE DERIVABILIDAD: EJERCICIO INTERESANTE DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 2º DE BACHILLERATO

EJERCICIO M2BE2207:

Sea la función f: ℜ→ℜ definida por:

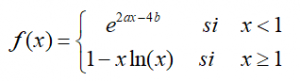
a.- Determinar los valores de a y b para que sea derivable.

b.- Hallar la ecuación de la recta tangente a la gráfica de f en el punto de abscisa x=2

EJERCICIO M2BE2255:

Se considera la función:

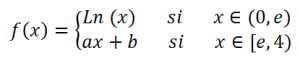
donde a y b son números reales.

Encuentre el valor de a y de b para que la función sea continua y derivable en el intervalo (0,4).

IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA

EJERCICIO M2BE2610:

Calcula el parámetro “a” para que la función definida a continuación sea derivable en todo ℜ.

IR AL ARTÍCULO CON LA RESOLUCIÓN DETALLADA DEL EJERCICIO: PRUEBA RESUELTA DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II, DE 2º BACHILLERATO CIENCIAS. PRIMER TRIMESTRE 2024-25

EJERCICIOM2BECS2948:

La rentabilidad (en %) de un fondo de inversión inmobiliario se obtiene mediante la función:

donde 𝑡 es el tiempo (en años) que el dinero permanece invertido en el fondo.

a) ¿Es continua la función de rentabilidad? Justifica la respuesta.

b) ¿Cuándo crece y cuando decrece esta función? Justifica la respuesta ¿Para qué valor de t se alcanza la rentabilidad máxima? ¿Cuánto vale dicha rentabilidad? Representa gráficamente la función.

c) ¿Es derivable la función R(t)?

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMENES RESUELTOS DE PROBABILIDAD, ESTADÍSTICA Y ANÁLISIS DE FUNCIONES, PARA MATEMÁTICAS II APLICADAS A LAS CIENCIAS SOCIALES DE 2º DE BACHILLERATO. SEGUNDO TRIMESTRE 2024-25

MÁS RECURSOS PARA MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS: MATEMÁTICAS 1º BACHILLERATO CIENCIAS

ASPECTOS FORMALES L.O.M.L.O.E. PARA DOCENTES:

SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS: