CÁLCULO INTEGRALES MATEMÁTICAS BACHILLERATO
CÁLCULO DE INTEGRALES,
PARA MATEMÁTICAS DE BACHILLERATO:

Hay operaciones muy relacionadas, no se puede entender la existencia de unas sin la otras, después de sumar si quieres regresar necesitas restar, en cambio si multiplicas para volver a tu origen debes dividir, y así, podríamos emparejar diversas funciones, las potencias con las raíces, la exponencial con el logaritmo, el seno, el coseno y la tangente con sus respectivos arcos, todo fluye de una manera perfecta de una lado para otro, como también ocurre con la integral y la derivada, la una sin la otra no podrían convivir en el universo matemático.
Cuando resolvemos una integral nos preguntamos… ¿de quién eres tú la derivada?… buscamos por lo tanto primitivas.
Y como no podría ser de otra forma, en este proyecto en el que estamos muy preocupados por la COMUNICACIÓN LINGÜISTICA, no podemos dejar de comentar lo siguiente:
PALABRAS PRIMITIVAS Y DERIVADAS:
Palabra primitiva es aquella palabra original, que no procede de otra.
Por ejemplo: Flor, Árbol, Jardín, Deporte…
Palabra derivada es aquella que no es original, sino que se forma a partir de una palabra primitiva.
Marino (procede de mar); panadería (procede de pan); leñador (procede de leña); verdoso (procede de verde) .
¡Qué casualidad!… ¿o no?
Volvemos a matemáticas…:
EJERCICIO M1BE2018:
En el vídeo del enlace se resuelven las siguientes integrales:
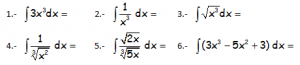
Resolución de integrales de tipo potencial: https://youtu.be/2HNCMQqS2n8
EJERCICIO M2BE2019:
En el video del enlace se resuelven las siguientes integrales:
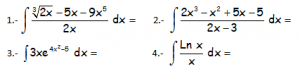
Dos integrales racionales y otras dos casi inmediatas: https://youtu.be/r00LK5Y8uG0
EJERCICIO M2BE2016:
Realiza el cálculo de las siguientes integrales:
![]()
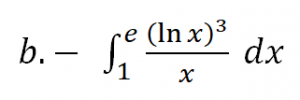
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/Hw08pifnAwo
MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE:
EJERCICIO M2BE2069:
Resolver la siguiente integral:
![]()
VÍDEO CON LA SOLUCIÓN DE LA INTEGRAL: https://youtu.be/TBl-DrEM0Hg
EJERCICIO M2BE2070:
Resolver la integral del ejercicio anterior (M2BE2069), utilizando la sustitución alternativa propuesta en su vídeo y comprobando que se obtiene el mismo resultado. Tomar una decisión personal al respecto del tipo de sustitución que se prefiere en estos casos de raíces cuadradas. Yo ya tomé la mía, ahora te toca a tí.
EJERCICIO M2BE2071:
Resolver la siguiente integral:
![]()
VÍDEO CON LA SOLUCIÓN DE LA INTEGRAL: https://youtu.be/kAPXuu981q4
EJERCICIO M2BE2073:
Resolver la siguiente integral:
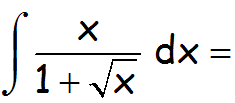
VÍDEO CON LA SOLUCIÓN DE LA INTEGRAL: https://youtu.be/HCB8XlaXafE
MÉTODO DE INTEGRACIÓN POR PARTES:
INTRODUCCIÓN. JUSTIFICACIÓN DE LA FÓRMULA:
VÍDEO CON LA JUSTIFICACIÓN DE LA FÓRMULA DEL MÉTODO DE INTEGRACIÓN POR PARTES: https://youtu.be/ek4Vn0XbtCc
EJERCICIO M2BE2067:
Resolver la siguiente integral indefinida:
![]()
VÍDEO CON LA SOLUCIÓN DE LA INTEGRAL: https://youtu.be/CABeLbOztnU
EJERCICIO M2BE2068:
Resolver la siguiente integral indefinida:
![]()
VÍDEO CON LA SOLUCIÓN DE LA INTEGRAL: https://youtu.be/GzGZzBr8e4k
EJERCICIO M2BE2128:
Calcular la siguiente integral indefinida:
![]()
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/NEj0QkFTQ7g
EJERCICIO M2BE2323:
Calcular la siguiente integral indefinida:
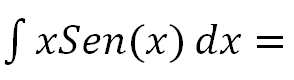
IR A LA SOLUCIÓN DE ESTA INTEGRAL
EJERCICIO M2BE2132:
Calcular la siguiente integral indefinida:
![]()
ARTÍCULO CON LA SOLUCIÓN DE LA INTEGRAL Y OTROS EJERCICIOS DE INTERÉS: PRUEBA DE ANÁLISIS Y ÁLGEBRA DE MATRICES PARA 2º BACHILLERATO
EJERCICIO M2BE2288:
Calcular la siguientes integral indefinida:
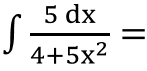
IR A LA RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL
EJERCICIO M2BE2297:
Calcular la siguiente integral indefinida:
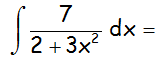
IR A LA RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL
EJERCICIO M2BE2289:
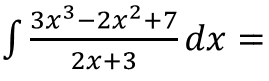
IR A LA RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL
EJERCICIO M2BE2298:
Calcular la siguiente integral indefinida:
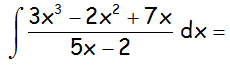
IR A LA RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL
EJERCICIOS M2BE1890:
Resolver las siguientes integrales:
EJERCICIOS M2BE2074:
Resolver las siguientes integrales:
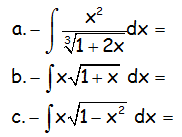
EJERCICIOS M2BE2075:
Resolver las siguientes integrales:
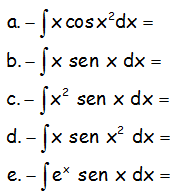
EJERCICIO M2BE2101:
Resolver las siguientes integrales:
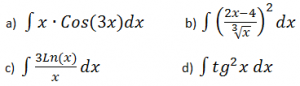
IR A A RESOLUCIÓN DE ESTE EJERCICIO EN: EXAMEN BLOQUE ANÁLISIS MATEMÁTICAS II. 2º BACHILLERATO
NOTA CURIOSA: La integral c, aparte de por sustitución, o incluso a través de la expresión de la función de la que es la derivada (ver tabla al final del artículo), se puede realizar por partes, generando una integral de las denominadas «cíclicas».
EJERCICIO M2BE2222:
Realiza las siguiente integrales indefinidas:

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTAS INTEGRALES INDEFINIDAS: EXAMEN FINAL GLOBAL MATEMÁTICAS 2º BACHILLERATO
EJERCICIO M2BE2299:
Calcular la siguiente integral indefinida:
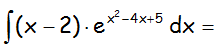
IR A LA RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL
EJERCICIO M2BE2300:
Calcular la siguiente integral indefinida:
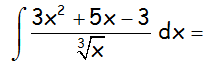
IR A LA RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL
EJERCICIO M2BE2302:
Resolver las siguientes integrales indefinidas:
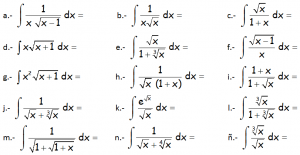
IR A LAS SOLUCIONES DE ESTAS INTEGRALES: EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
EJERCICIO M2BE2318:
Calcular la siguiente integral indefinida:
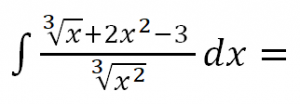
EJERCICIO M2BE2319:
Calcular la siguiente integral indefinida:
![]()
EJERCICIO M2BE2320:
Calcular la siguiente integral indefinida:
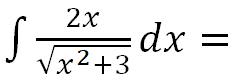
EJERCICIO M2BE2379:
Calcular la siguiente integral indefinida:
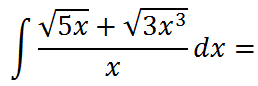
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL INDEFINIDA: EXAMEN ANÁLISIS, ÁLGEBRA Y GEOMETRÍA PARA MATEMÁTICAS DE 2º DE BACHILLERATO
EJERCICIO M2BE2380:
Calcular la siguiente integral indefinida:
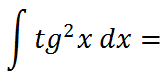
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA INTEGRAL INDEFINIDA: EXAMEN ANÁLISIS, ÁLGEBRA Y GEOMETRÍA PARA MATEMÁTICAS DE 2º DE BACHILLERATO
EJERCICIO M2BE2270 EBAU CANARIAS JUNIO 2023:
Hallar la función polinómico f(x) que verifica que tiene un punto mínimo en M (1,2) y su segunda derivada es:
f»(x) = 2x + 3
Dar la expresión de f(x).
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: MATEMÁTICAS II. E.B.AU. CANARIAS 2023. EJERCICIOS RESUELTOS. CONVOCATORIA ORDINARIA JUNIO
EJERCICIO M2BE2442:
Hallar la función polinómica 𝑓(𝑥) que verifica que tiene un punto mínimo en 𝑀(2,-10) y su segunda derivada es: f’’(x) = x + 4 . Dar la expresión de 𝑓(𝑥).
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN TERCER TRIMESTRE MATEMÁTICAS II DE 2º DE BACHILLERATO: ANÁLISIS, ÁLGEBRA, GEOMETRÍA, PROBABILIDAD
UTILIZACIÓN DE LA INTEGRAL DEFINIDA PARA EL CÁLCULO DE ÁREAS:
TEORÍA Y EJERCICIOS PARA CÁLCULO DE ÁREAS CON INTEGRALES DEFINIDAS
EJERCICIOS PROPUESTOS DE CÁLCULO DE ÁREAS:
EJERCICIO M2BE2072:
La finca de la familia Sarandonga está delimitada por la función f(x)=x3+x2-2x y el eje OX, o el eje X, o el eje de abscisas, o como tú quieras designarlo. La finca está dividida en dos partes, ya que el río Arzúa, que pasa exactamente por el eje Y, hace una división natural de la misma. La parte izquierda del río la va a heredar Alberto y la parte derecha JL, dos hermanos de distinto padre y madre que no se llevan muy bien que digamos. Haz un esbozo de la finca. ¿Qué porcentaje de la finca heredó cada uno de los hermanos?
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/JtbE5rsDeS4
ESTE EJERCICIO FORMA PARTE DE UN EXAMEN DE MATEMÁTICAS DE 2º DE BACHILLERATO QUE INCLUYE TODOS LOS CONTENIDOS. PARA SU CONSULTA SI SE DESEA: https://achimagec.com/examen-matematicas-2o-bachillerato-ciencias/
EJERCICIO M2BE2171:
Realizar una representación gráfica del área encerrada por las funciones f(x) = x2 – 3x y g(x) = – x. Calcular el área de la región.
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTE EJERCICIO: EXAMEN BLOQUES ANÁLISIS, ÁLGEBRA Y GEOMETRÍA. MATEMÁTICAS II. 2º BACHILLERATO
EJERCICIO M2BE2192:
La finca Los Naranjos, está delimitada por las funciones f(x) = x3 – 6x2 + 9x y g(x) = 4x. Los Naranjos tiene dos regiones, la región 1 (a la izquierda) y la región 2 (a la derecha). La región 1 es urbanizable, con un valor de 8000 euros el metro cuadrado, y la región 2 es rústica, por lo tanto, el valor del metro cuadrado es mucho menor, exactamente 187.5 euros el metro cuadrado. Si las regiones se venden independientemente, ¿Qué región aconsejarías que se comprara? ¿Por qué? Dibuja la finca Los Naranjos.
IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: PRUEBA DE EXAMEN DE MATEMÁTICAS II, 2º DE BACHILLERATO. ANÁLISIS, ÁLGEBRA DE MATRICES, GEOMETRÍA Y PROBABILIDAD
EJERCICIO M2BE2291:
Un agricultor llamado Saúl, quiere comprar un terreno rústico en Teror.
El terreno, está limitado por la función f(x) = x3 + 6x2 – x – 30 y el eje OX. Supongamos que el gráfico está en metros.
a) Realiza un gráfico del terreno que quiere comprar Saúl.
b) Calcula el precio del terreno, si cada metro cuadrado en Teror tiene un valor de 6500 euros. Si Saúl dispone de 600000 euros. ¿Puede comprarlo?
IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ÁREAS
EJERCICIO M2BE2225: EBAU CANARIAS 2011
Dadas las funciones: y = – x2 + 4x e y = 2x2 – 2x
a.- Representar la región que determinan sus gráficas.
b.- Calcular el área de dicha región.
IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2301:
Un agricultor llamado Saúl, quiere comprar un terreno rústico en Teror. El terreno, está limitado por la función:
f(x) = x3 – 13x + 12
y el eje OX. Supongamos que el gráfico está en metros.
a.- Realiza un gráfico del terreno que quiere comprar Saúl.
b.- Calcula el precio del terreno, si cada metro cuadrado en Teror tiene un valor de 6500 euros. Si Saúl dispone de 700000 euros, ¿puede comprarlo?.
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE CÁLCULO DE ÁREAS
EJERCICIOS M2BP187:
1. Calcula el área del recinto limitado por la parábola y = x2 , y las rectas: y = 0, x = 2 , x = 6.
2. Calcula el área del recinto limitado por la parábola de ecuación y = 9 – x2 y el eje de abscisas.
3. Calcula el área del recinto limitado por la parábola y = 4x – x2 y el eje de abscisas en el intervalo [0,6].
4. Halla el área comprendida entre las parábolas f(x) = 8 – x2 , g(x) = x2
5. Halla el área del recinto limitado por la parábola de ecuación y = x2 , la recta de ecuación y = x+2 y el eje OX.
6. Calcula el área del recinto limitado por la curva de ecuación:
y la recta y = x.
7. Halla el área del recinto limitado por las gráficas de las funciones: y = ln x , y = 1 y los ejes de coordenadas.
IR A LAS SOLUCIONES DE ESTOS EJERCICIOS
EJERCICIO M2BE2278:
Un agricultor llamado OMAR, se compró un terreno rústico en Santa Brígida. El terreno, está limitado por las funciones:
f(x) = x2 – 4x + 4 y g(x) = – x2 + 4
Suponemos que el gráfico está en metros.
a.- Realiza un gráfico del terreno que adquirió Omar.
b.- Calcula el precio del terreno, si cada metro cuadrado en Santa Brígida tiene un valor aproximado de 18500 euros. Alberto dice que costó menos de 48000 euros ¿está en lo cierto?.
IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24
EJERCICIO M2BE2321:
Un agricultor llamado Hortensio, quiere comprar un terreno rústico en Moya. El terreno, está delimitado por las funciones f(x) = x2 – 4x + 4 y g(x) = x. Suponiendo que el gráfico está en hectómetros:
a) Realiza un gráfico del terreno que quiere comprar Hortensio y sombréalo.
b) Calcula el precio del terreno, si cada hectómetro cuadrado en Moya tiene un valor de 150250 euros. Si Hortensio dispone de 600000 euros. ¿Puede comprarlo?
SOLUCIÓN DE ESTE EJERCICIO DE CÁLCULO DE ÁREAS UTILIZANDO LA INTEGRAL DEFINIDA
EJERCICIO M2BE2356:
Otra vez, otro agricultor, que ahora se llama Gervasio, quiere comprar otro terreno rústico, esta vez en Fontanales. El terreno, está delimitado por las funciones f(x) = x2 – 4x + 4 y g(x) = – 2x + 7. Suponiendo que el gráfico está en hectómetros.
a) Realiza un gráfico del terreno que quiere comprar Gervasio y sobréalo.
b) Calcula el precio del terreno, sabiendo que cada hectómetro cuadrado en Fontanales tiene un valor de cincuenta y seis mil euros. Gervasio dispone de 600000 euros. ¿Puede comprarlo?
IR A LA RESOLUCIÓN DE ESTE EJERCICIO DE CÁLCULO DE ÁREAS, UTILIZANDO LA INTEGRAL DEFINIDA
EJERCICIO M2BE2422:
Dibuja y calcula el área encerrada entre la función f(x) = x2 – 4x y g(x) = 3 – 2x.
IR AL ARTÍCULO QUE CONTIENE LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE CÁLCULO DE ÁREAS CON LA INTEGRAL DEFINIDA: EXAMEN DE ANÁLISIS DE FUNCIONES, ÁLGEBRA, GEOMETRÍA ESPACIAL Y PROBABILIDAD PARA MATEMÁTICAS II DE 2º BACHILLERATO
EJERCICIO M1BE2455:
Hallar el área encerrada por las función y = -x2 + 3 y el eje OX
EJERCICIO M1BE2456:
Hallar el área encerrada por las funciones f(x) = x , x=3 y el eje OX
EJERCICIO M1BE2457:
Hallar el área encerrada por y = x3 – x y el eje OX.
EJERCICIO M1BE2458:
Calcular el área comprendida entre la gráfica de la función y = x3 – 6x2 + 8x y el eje OX, haciendo un dibujo aproximado y explicando.
EJERCICIO M1BE2459:
Dada la parábola de ecuación y = 4 – x2 y la recta de ecuación y = x + 2
a.- Hallar los puntos de intersección entre las funciones anteriores.
b.- Esbozar el gráfico señalando el recinto limitado por ambas funciones.
c.- Calcular el área del recinto limitado por las dos funciones.
EJERCICIO M1BE2460:
Dibuja el recinto limitado por las funciones f(x) = 2x2 – 4x +3 y g(x) = x2 – 2x + 3 y calcula el área de este recinto.
POR SI NOS RESULTA COMPLICADO LA REPRESENTACIÓN DE LAS FUNCIONES IMPLICADAS EN ESTOS TIPOS DE EJERCICIOS, SE RECOMIENDA LA CONSULTA DEL SIGUIENTE ARTÍCULO, CON RECURSOS AUDIOVISUALES:
REPRESENTACIÓN DE FUNCIONES PARA 1º DE BACHILLERATO
PODRÍA INTERESAR ECHARLE UN VISTAZO AL SIGUIENTE ARTÍCULO DE ESTA MISMA WEB: INTEGRALES EN FÍSICA
EJERCICIOS PROPUESTOS DE INTEGRALES INDEFINIDAS:
H. INTEGRAL INDEFINIDAEJERCICIOS PROPUESTOS DE INTEGRALES DEFINIDAS, CÁLCULO DE ÁREAS:
I. ACTIV INTEGRAL DEFINIDATABLA DE INTEGRALES:
TABLA INTEGRALES
Comments are closed, but trackbacks and pingbacks are open.