EXAMEN ANÁLISIS ÁLGEBRA BACHILLERATO
MATEMÁTICAS II 2º BACHILLERATO
EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º BACHILLERATO (X663). SEGUNDO TRIMESTRE,
REALIZADO EN «EL PILAR»:

PUEDE INTERESAR LA CONSULTA DE:
-
- MATRICES Y DETERMINANTES PARA BACHILLERATO.
- DISCUSIÓN Y RESOLUCIÓN DE SISTEMAS LINEALES. ROUCHÉ Y CRAMER
- FUNCIONES: ANÁLISIS PARA 1º BACHILLERATO
- APLICACIONES DE LA DERIVADA. OPTIMIZACIÓN Y CÁLCULO DE PARÁMETROS.
- INTEGRALES Y DERIVADAS. PROBLEMAS CONTEXTUALIZADOS
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
ESTA PRUEBA SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA
EXAMEN ANÁLISIS ÁLGEBRA MATEMÁTICAS 2º BAC 23 24 2 TRIM_V1LOS EJERCICIOS DE LA PRUEBA Y SU RESOLUCIÓN PASO A PASO:
EJERCICIO M2BE2353:
Siendo A y B las matrices siguientes:
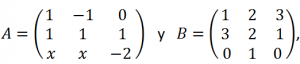
a) ¿Para qué parámetros x la matriz C=AB tiene inversa.
b) Si es posible, calcula la inversa de C cuando x=2.
LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE OPERACIONES CON MATRICES:
EJERCICIO M2BE2353 MATRICES_v1EJERCICIO M2BE2354:
a) Discutir según el parámetro a el siguiente sistema de ecuaciones lineal de tres ecuaciones y tres incógnitas.
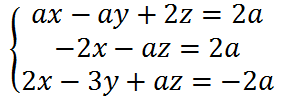
b) Resolver, si es posible, para a =-2.
LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE DISCUSIÓN Y RESOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES:
M2BE2354 DISCUSIÓN RESOLUCIÓN SISTEMAS ECUACIONES ROUCHE_v1EJERCICIO M2BE2355:
Considera la función f(x) = ax3 + bx2 + cx + d.
Calcular los coeficientes a, b, c y d, sabiendo que f tiene un extremo relativo en el punto P(0,1) y su gráfica tiene un punto de inflexión Q(1, -1)
Dar la expresión de la función f(x).
LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE PARÁMETROS Y APLICACIONES DE LA DERIVADA:
M2BE2355 PARÁMETROS APLICACIONES DE LA DERIVADA_v1EJERCICIO M2BE2356:
Otra vez, otro agricultor, que ahora se llama Gervasio, quiere comprar otro terreno rústico, esta vez en Fontanales. El terreno, está delimitado por las funciones f(x) = x2 – 4x + 4 y g(x) = – 2x + 7. Suponiendo que el gráfico está en hectómetros.
a) Realiza un gráfico del terreno que quiere comprar Gervasio y sobréalo.
b) Calcula el precio del terreno, sabiendo que cada hectómetro cuadrado en Fontanales tiene un valor de cincuenta y seis mil euros. Gervasio dispone de 600000 euros. ¿Puede comprarlo?
2356 cálculo áreas integral definida_v1