FINAL GLOBAL MATEMÁTICAS BACHILLERATO
MATEMÁTICAS II 2º BACHILLERATO
EXAMEN FINAL GLOBAL MATEMÁTICAS 2º BACHILLERATO. INCLUYE GEOMETRÍA, ANÁLISIS, ÁLGEBRA, PROBABILIDAD,
REALIZADO EN «EL PILAR»:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES MATERIALES DENTRO DE ESTE PROYECTO DE MEJORA DEL APRENDIZAJE EN CIENCIAS:
ESTA PRUEBA SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA:
EXAMEN FINAL GLOBAL MATEMÁTICAS 2º BACHILLERATOEJERCICIO M2BE2217:
Considere el plano π:
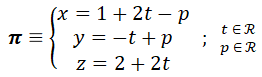
y la recta r que pasa por los puntos P(1, 0, 6) y Q(1, 2, -3).
a) Estudiar la posición relativa del plano y la recta r.
b) Calcular la recta s, que es perpendicular a la recta r y pasa por el punto J(0, -5, -14).
EJERCICIO M2BE2217 GEOMETRÍA EN EL ESPACIOEJERCICIO M2BE2218:
a.- Discute según el parámetro a el siguiente sistema de ecuaciones:
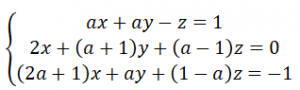
b.- Resolver cuando sea posible.
SOLUCIÓN PASO A PASO DEL EJERCICIO:
DISCUSION SISTEMA DE ECUACIONES 2218 ROUCHEEJERCICIO M2BE2219:
En un banco se sabe que el tiempo de devolución de un préstamo de 25000 € sigue una distribución normal de media 5 años y desviación típica 8 meses. Se elige al azar un préstamo de 25000 € realizado en dicho banco.
a) Calcular la probabilidad de que dicho préstamo se devuelva como mucho en 70 meses.
b) El banco afirma, que más de un 85% de los préstamos se formalizan entre los 4 y los 6 años, ¿Es cierto?
EJERCICIO M2BE2219 DISTRIBUCION NORMAL PROBABILIDADEJERCICIO M2BE2220:
Una empresa ha llevado a cabo un proceso de selección de personal. Se sabe que el 40% del total de aspirantes han sido seleccionados en el proceso.
a) Si entre los aspirantes había un grupo de 8 amigos, calcule la probabilidad de que al menos 2 de ellos hayan sido seleccionados.
b) Si entre los aspirantes había un grupo de 45 amigos, calcule la probabilidad de que como máximo hayan sido seleccionados 20 amigos.
EJERCICIO M2BE2220 BINOMIAL APROXIMACIÓN NORMALEJERCICIO M2BE2221:
Se dispone de un hilo metálico de longitud 140 m. Se quiere dividir dicho hilo en tres trozos de forma que la longitud de uno de los trozos sea el doble de la longitud de otro y tal que, al construir con cada uno de los tres trozos de hilo un cuadrado, la suma de las áreas de los tres cuadrados sea mínima. Encontrar la longitud de cada trozo.
SOLUCIÓN DEL EJERCICIO DE OPTIMIZACIÓN:
EJERCICIO M2BE2221 PROBLEMA DE OPTIMIZACIÓNEJERCICIO M2BE2222:
Realiza las siguiente integrales indefinidas:
SOLUCIÓN DE LAS INTEGRALES:
EJERCICIO M2BE2222 INTEGRALES INDEFINIDAS