EXAMEN BLOQUES ANÁLISIS, ÁLGEBRA Y GEOMETRÍA. MATEMÁTICAS II. 2º BACHILLERATO

EXAMEN ANÁLISIS ÁLGEBRA GEOMETRÍA

MATEMÁTICAS II 2º BACHILLERATO

PRUEBA DE EXAMEN DE LOS BLOQUES DE ANÁLISIS, ÁLGEBRA DE MATRICES Y GEOMETRÍA, PARA MATEMÁTICAS II, DE 2º DE BACHILLERATO, REALIZADA EN «EL PILAR»:

ESTA PRUEBA SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA

Los Enunciados de la prueba (X649), que incluyen aspectos de AUTOEVALUACIÓN e INFORMACIÓN DE RETORNO (FEED-BACK):

X649 GLOBAL EVALUACION 2 22 23

LOS EJERCICIOS DE LA PRUEBA, CON LA RESOLUCIÓN:

EJERCICIO M2BE2167:

Sean los puntos A(3, 1, 5), B(-2, -1, 4) y C(2, 3, 2).

Calcular la ecuación en forma general del plano π que contiene a los tres puntos.

ejercicio m2be2167

EJERCICIO M2BE2159 modificado:

Sean los puntos A (3, 1, 5) y B (-2, -1, 4). Calcular la recta s perpendicular a la recta determinada por A y B, sabiendo que s pasa por P(-2, 3, -1).

EJERCICIO M2BE2159 SOLUCIÓN GEOMETRÍA ok

EJERCICIO M2BE2168:

Sean los puntos B(-2, -1, 4) y C(2, 3, 2). Calcular la posición relativa de la recta m que pasa por B y C, y la recta n:

EJERCICIO M2BE2168 GEOMETRÍA RECTAS

EJERCICIO M2BE2169:

a.- Discutir el siguiente sistema de ecuaciones según el parámetro real m:

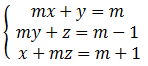
b.- Resolver en los casos posibles.

EJERCICIO M2BE2169 DISCUSIÓN SISTEMAS

ARTÍCULO DEL PROYECTO CON MATERIALES RELACIONADOS CON DISCUSIÓN DE SISTEMAS DE ECUACIONES DE INTERÉS: DISCUSIÓN Y RESOLUCIÓN DE SISTEMAS LINEALES. ROUCHÉ Y CRAMER

EJERCICIO M2BE2170:

Resolver la ecuación matricial siguiente: XA + B^t = C, sabiendo que:

EJERCICIO M2BE2170 ECUACIONES MATRICES

ARTÍCULO DEL PROYECTO CON MATERIALES RELACIONADOS CON ECUACIONES MATRICIALES DE INTERÉS: RESOLUCIÓN DE ECUACIONES Y SISTEMAS DE ECUACIONES MATRICIALES

EJERCICIO M2BE2161:

Calcula los parámetros a y b para que la función definida a continuación sea derivable en todo ℜ.

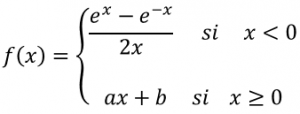
SOLUCIÓN DEL EJERCICIO M2BE2161:

EJERCICIO M2BE2161 DERIVABILIDAD

EJERCICIO M2BE2171:

Realizar una representación gráfica del área encerrada por las funciones  f(x) = x² – 3x   y   g(x) = – x. Calcular el área de la región.

EJERCICIO M2BE2171 INTEGRALES ÁREAS

ARTÍCULO DE ESTE PROYECTO CON MATERIALES RELACIONADOS CON CÁLCULO DE ÁREAS CON INTEGRALES DE INTERÉS: CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO