REPASO ANÁLISIS MATEMÁTICAS BACHILLERATO
ANÁLISIS DE FUNCIONES PARA PRIMERO DE BACHILLERATO:
Ejercicios de repaso final para preparar una prueba global de ANÁLISIS DE FUNCIONES, para MATEMÁTICAS de 1º de Bachillerato.
PUEDE INTERESAR IR A:
https://achimagec.com/representacion-de-funciones-especiales-las-pardelas/
https://achimagec.com/ejercicios-de-analisis-de-funciones/
https://achimagec.com/funciones-limites-derivadas-y-aplicaciones/
https://achimagec.com/propuesta-de-evaluacion-funciones-1o-bachillerato/
EJERCICIO M1BE2004:
Considera la función:
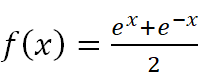
a) Estudia y determina los intervalos de crecimiento y los intervalos de decrecimiento de f. Calcula los extremos relativos de f (abscisas donde se obtienen y valores que se alcanzan).
b) Halla la ecuación de la recta normal a la gráfica de f en el punto de abscisa x = 0.
EJERCICIO M1BE2005:
Considera la región limitada por las curvas:
![]()
a) Esboza la gráfica de la región dada, hallando los puntos de corte de ambas curvas.
b) Expresa el área como una integral.
c) Calcula el área.
EJERCICIO M1BE2006:
Se desea construir un depósito con forma de prisma regular de base cuadrada. Además, el depósito es abierto (sin tapa superior). La capacidad total debe ser de 64 m3. El material de construcción de los laterales tiene un precio de 70 euros por m2, mientras que el de la base, más resistente, es de 140 euros por m2. Halle las dimensiones del depósito para que tenga el menor coste posible.
EJERCICIO M1BE2007:
Halla a>0 y b>0 sabiendo que la gráfica de la función f: ℜ→ℜ, dada por:
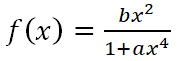
tiene en el punto (1, 2) un punto crítico.
EJERCICIO M1BE2008:
Se sabe que la gráfica de la función f definida por:

(para x≠1) tiene una asíntota oblicua que pasa por el punto (1, 1) y tiene pendiente 2. Calcula a y b.
EJERCICIO M1BE2009:
Calcular los siguientes límites:
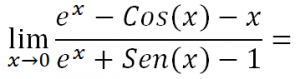
VÍDEO QUE RESUELVE ESTE LÍMITE: https://youtu.be/cM8Yr-Sq1tU
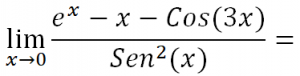
VÍDEO QUE RESUELVE ESTE SEGUNDO LÍMITE: https://youtu.be/r4awczVeiaY
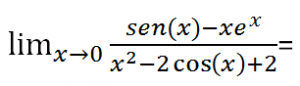
VÍDEO QUE RESUELVE ESTE TERCER LÍMITE: https://youtu.be/YwALjvQsJ7s
EJERCICIO M1BE2010:
Considera la función continua definida por f: ℜ→ℜ
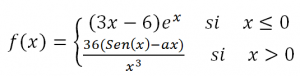
a) Calcula a.
b) Halla la ecuación de la recta tangente a la gráfica f en el punto de abscisa x=-1.
REPRESENTACIÓN DE LA SITUACIÓN CON GEOGEBRA:
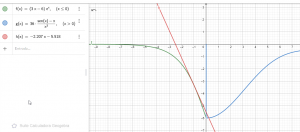
EJERCICIO M1BE2011:
Considera la función f: definida por f: ℜ→ℜ, f(x) = 4x3 – x4.
a) Determina los intervalos de crecimiento y de decrecimiento de f.
b) Esboza la gráfica de f y calcula el área del recinto limitado por dicha gráfica y el eje de abscisas.
EJERCICIO M2BE1753:
Para la función: f(x) = x + x · e-x , calcular la ecuación de la recta tangente a ella, en un punto de abscisa en el cual dicha recta tangente sea paralela a la recta que pasa por (0,0) y (2,2).
IR A LA RESOLUCIÓN DEL EJERCICIO
EJERCICIO M2BE1826:
Hallar el siguiente límite:
EJERCICIO M2BE1827:
Hallar el siguiente límite:
EJERCICIO M2BE1828:
Hallar el siguiente límite:
IR A LA RESOLUCIÓN DE ESTOS TRES ÚLTIMOS LÍMITES
EJERCICIO M2BE2012:
Estudiar el dominio de las siguientes funciones,
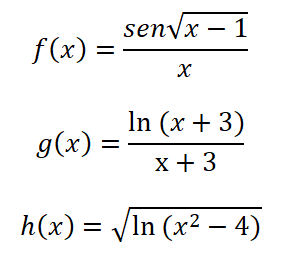
VÍDEO QUE RESUELVE EL ÚLTIMO DOMINIO: https://youtu.be/cC5UsrLQb0g
EJERCICIO M2BE309:
El dueño de un manantial de agua mineral llega a la siguiente conclusión: si el precio a que vende la botella es x euros, sus beneficios serán de –x2+10x-21 miles de euros al mes. Hallar:
a) ¿Qué precio debe poner para obtener un beneficio máximo?
b) ¿Cuál será ese beneficio?
c) ¿Entre que precios obtiene beneficios el agricultor?
d) Representar la función.
IR A LA RESOLUCIÓN DE ESTE EJERCICIO
EJERCICIO M2BE395:
Se desea cerrar con una cuerda dos parcelas rectangulares adyacentes (consecutivas) e iguales que encierran entre las dos un área de 1000 m2.
a) Encontrar la función que da la longitud de cuerda necesaria para cerrarlas.
b) ¿Cómo deben ser las parcelas para que el gasto de cuerda sea mínimo?
IR A LA RESOLUCIÓN DE ESTE EJERCICIO
EJERCICIOS M1BE2013:
IR A RELACIÓN DE PROBLEMAS DE OPTIMIZACIÓN CON SOLUCIÓN
EJERCICIO M1BE2014:
Hallar los coeficientes a, b y c sabiendo que la función definida por f(x)=x3+ax2+bx+c tiene en x=1 un punto de derivada nula que no es extremo relativo y que la gráfica de f pasa por el punto (1,1).
EJERCICIO M1BE2015:
Para la siguiente función:
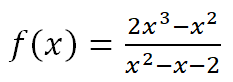
a.- Estudiar el dominio de definición y calcule las asíntotas horizontales, verticales y oblicuas caso de existir.
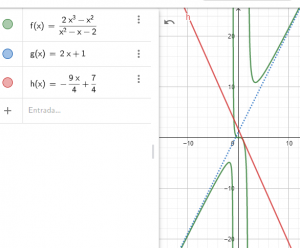
b.. Calcular la recta tangente a la curva en el punto x=1
EJERCICIO M2BE2017:
Dada la función:
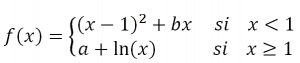
a.- Estudia los valores de los parámetros a y b para que la función f(x) sea continua y derivable en ℜ. Escribe la función resultante f(x).
b.- Tomando los valores a=-2 y b=1, calcula la ecuación de la recta tangente en x=e.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/foUIAm2GnC4
IR A CONTENIDOS DE MATEMÁTICAS DE 1º BACHILLERATO
RECURSOS PARA MATEMÁTICAS II DE 2º DE BACHILLERATO:
ESTE MATERIAL TIENE RELACIÓN CON ASPECTOS DEL PERFIL DE SALIDA DEL ALUMNADO DE LOS INSTITUTOS DIOCESANOS DE CANARIAS

Comments are closed, but trackbacks and pingbacks are open.