EXAMEN FINAL ANÁLISIS FUNCIONES

EXAMEN FINAL DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO, REALIZADO EN «EL PILAR»:

INTERESA LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS, CORRESPONDIENTES A ESTE PROYECTO DE MEJORA DEL APRENDIZAJE EN CIENCIAS:

SIGUE EL PROCESO DETERMINADO SEGÚN: MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA

LOS ENUNCIADOS DE LA PRUEBA DE ANÁLISIS DE FUNCIONES, QUE INCLUYEN ASPECTOS DE AUTOEVALUACIÓN DEL ALUMNADO E INFORMACIÓN DE RETORNO (FEEDBACK ADICIONAL EN PRUEBAS EVALUADORAS):

EXAMEN FINAL ANÁLISIS FUNCIONES MATEMÁTICAS I 1º BACHILLERATO

LOS EJERCICIOS DE LA PRUEBA CON LA RESOLUCIÓN PASO A PASO Y/O MATERIALES AUDIOVISUALES QUE LOS RESUELVEN:

LA VARIEDAD EN LA PRESENTACIÓN DE FORMATOS DEBE CONSIDERARSE ACORDE CON LAS DIRECTRICES DEL «DISEÑO UNIVERSAL PARA EL APRENDIZAJE (D.U.A.)«

EJERCICIO M1BE2266:

Calcular el siguiente límite:

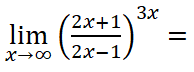
RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE LÍMITES:

EJERCICIO MIBE2266 LÍMITE NÚMERO e

EJERCICIO M1BE2267:

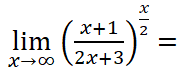
RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE LÍMITES:

EJERCICIO MIBE2267 LÍMITE DIRECTO

EJERCICIO M1BE2268:

Para la siguiente función,

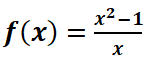
realizar los siguientes apartados:

a.- Dominio y cortes con los ejes

b.- Asíntotas.

c.- Monotonía

RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO:

EJERCICIO MIBE2268 FUNCIÓN RACIONAL

EJERCICIO M1BE2164:

Se quiere construir una ventana rectangular de 1 metro cuadrado de área. El coste del marco es de 12.5 euros por cada metro de altura y de 8 euros por cada metro de anchura. ¿Qué dimensiones debe tener la ventana para que el marco resulte lo más económico posible?

IR AL VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/ZOYcoL5CytU

CAPTURA DEL VÍDEO PARA FACILITAR LA INMEDIATEZ EN LA CONSULTA Y LA PRESENTACIÓN DE LA SOLUCIÓN EN OTRO FORMATO SEGÚN LAS DIRECTRICES DEL «DISEÑO UNIVERSAL PARA EL APRENDIZAJE (D.U.A.)«

EJERCICIO M1BE2164 OPTIMIZACIÓN CAPTURA VÍDEO JL

EJERCICIO M1BE2028:

Determinar una función de la forma f(x) = x³+ax²+bx+c ,que tenga un extremo relativo en el punto de abscisa x=2 y para la cual el punto P(1, 2) sea un punto de inflexión.

VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/z5oCkg4bWTQ

CAPTURA DEL VÍDEO PARA FACILITAR LA INMEDIATEZ EN LA CONSULTA Y LA PRESENTACIÓN DE LA SOLUCIÓN EN OTRO FORMATO SEGÚN LAS DIRECTRICES DEL «DISEÑO UNIVERSAL PARA EL APRENDIZAJE (D.U.A.)«

EJERCICIO M1BE2128 PARÁMETROS CAPTURA VÍDEO JL

EJERCICIO M1BE2269:

Representar con los datos necesarios (dominio, cortes, extremos relativos y punto de inflexión) la función :

f(x) = 3x³+ x²– 12x – 4

RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO:

EJERCICIO MIBE2269 REPRESENTACIÓN FUNCIÓN POLINÓMICA

Post Views: 1.045