EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO

EXAMEN ANÁLISIS MATEMÁTICAS BACHILLERATO

DOMINIOS LÍMITES ASÍNTOTAS DERIVADAS

EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS DE 1º DE BACHILLERATO, REALIZADO EN «EL PILAR»:

Primera prueba de este contenido, que incluye obtención de límites, asíntotas, dominio, corte con los ejes, derivadas, monotonía, curvatura, máximos y mínimos, puntos de inflexión, obtención de derivada utilizando la definición.

Se contemplan aspectos relacionados con AUTOEVALUACIÓN DEL ALUMNADO e INFORMACIÓN DE RETORNO (FEED BACK) adicional en pruebas evaluadoras.

SIGUE EL PROCESO DETERMINADO SEGÚN: MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA

LOS ENUNCIADOS DE LA PRUEBA:

EXAMEN ANÁLISIS FUNCIONES MATEMÁTICAS 1º BACHILLERATO

LOS EJERCICIOS DE LA PRUEBA CON SUS SOLUCIONES:

EJERCICIO M1BE2194:

Hallar el límite de la siguiente función:

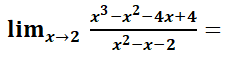
SOLUCIÓN DEL EJERCICIO PASO A PASO:

EJERCICIO M1BE2194 LÍMITES COCIENTE FACTORIZAR POLINOMIOS

EJERCICIO M1BE2195:

EJERCICIO M1BE2195 SOLUCIÓN LIMITE CONJUGADO

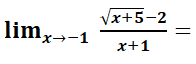
EJERCICIO M1BE2196:

Teniendo en cuenta la siguiente función :

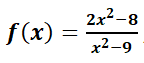
Hallar:

a.- Asíntotas.

b.- Corte con los ejes.

EJERCICIO M1BE2196 ESTUDIO FUNCIONES RACIONALES

EJERCICIO M1BE2197:

Siendo  f(x) = x³ – 3x² – x + 3 , obtener:

a.- Dominio y corte con los ejes.

b.- Monotonía y máximos y mínimos.

c.- Curvatura y puntos de inflexión.

d.- Representación gráfica.

EJERCICIO M1BE2197 REPRESENTACIÓN FUNCIONES POLINÓMICAS

EJERCICIO M1BE2198:

Realizar la derivada de la función  f(x) = x² + 5x – 3 , utilizando la definición de derivada.

EJERCICIO MIBE2198 DERIVADA POLINÓMICA DEFINICIÓN

SI BIEN LAS SOLUCIONES ESTÁN REALIZADAS BAJO EL CRITERIO DE LOS PROFESORES, PARA MEJORAR EL RIGOR, FORMALIDAD Y NOMENCLATURA MATEMÁTICAS, INCLUSO A UN NIVEL SUPERIOR AL DE LOS PROFESORES, ¿QUÉ CUESTIONES FALTAN EN EL DESARROLLO DE LAS SOLUCIONES DE LOS DIFERENTES EJERCICIOS PARA BORDAR EL EXAMEN?

LAS PROPUESTAS LAS COMENTAN EN CLASE Y PODRÍAN SER PREMIADAS.