GEOMETRÍA MATRICES PROBABILIDAD ANÁLISIS
EXAMEN GLOBAL MATEMÁTICAS II
EXAMEN GLOBAL MATEMÁTICAS II 2º BACHILLERATO. GEOMETRÍA, ÁLGEBRA DE MATRICES, PROBABILIDAD, ANÁLISIS (OPTIMIZACIÓN),
REALIZADO EN «EL PILAR»:

INTERESA LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS DENTRO DE ESTE PROYECTO DE MEJORA DEL APRENDIZAJE EN CIENCIAS:
ESTA PRUEBA SIGUE LA DINÁMICA QUE SE REFLEJA EN LA PROGRAMACIÓN PARA ESTE CURSO DE MATEMÁTICAS II DE 2º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA: MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
LOS ENUNCIADOS DE LA PRUEBA:
X652 EXAMEN MATEMÁTICAS II ANÁLISIS GEOMETRÍA MATRICES PROBABILIDAD GLOBAL 3TRIM 22 23LOS EJERCICIOS DE LA PRUEBA Y SUS SOLUCIONES PASO A PASO:
EJERCICIO M2BE2209:
Considere el plano π: x+y+z=1 y la recta r que pasa por los puntos P (0, 0, 6) y Q (1, 2, 3).
a.- Estudie la posición relativa de la recta r y el plano π.
b.- Calcular la recta s, perpendicular al plano , que pasa por el punto simétrico de P respecto de Q.
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M2BE2209 GEOMETRÍA PLANOS Y RECTAS EN EL ESPACIOEJERCICIO M2BE2210:
Sea A la siguiente matriz en la que a es un parámetro real:
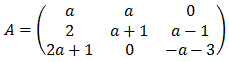
a.- Encuentra los valores de para los que la matriz A es invertible.
b.- Para a=3, resolver la ecuación matricial AX = B – 3I , donde B es la matriz:
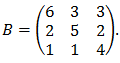
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M2BE2210 MATRIZ INVERSA ECUACIÓN MATRICIALEJERCICIO M2BE2211:
Una urna tiene en su interior 3 monedas: una rupia, una libra y una corona. La rupia tiene su cara y su cruz, la libra tiene cara por los dos lados y la corona está trucada, de forma que la probabilidad de salir cara es 1/5. Se tira una moneda elegida al azar.
a.- Calcular la probabilidad que se obtenga cara.
b.- Si ha salido cruz, ¿cuál es la probabilidad que sea la corona?
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M2BE2212 PROBABILIDAD DIAGRAMA ÁRBOL MONEDASEJERCICIO M2BE2212:
Se lanza un dado perfecto de seis caras en 600 ocasiones. Calcular la probabilidad de que el número de veces que salga el 5:
a.- Sea superior a 95.
b.- Esté comprendido entre 100 y 110.
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M2BE2212 LA BINOMIAL SE APROXIMA A LA NORMALEJERCICIO M2BE2213:
El propietario de una empresa ha estimado que si compra «x» máquinas y contrata «y» empleados, el número de unidades de producto que podría fabricar vendría dado por la función f(x, y) = 9xy2. Sabiendo que tiene un presupuesto de 22500 €, que cada máquina supone una inversión de 2500 € y cada contrato de un nuevo empleado 1 500 €, determine el número de obreros que debe contratar y el número de máquinas que debe comprar para optimizar la producción.
LA SOLUCIÓN PASO A PASO DEL EJERCICIO:
EJERCICIO M2BE2213 PROBLEMA OPTIMIZACIÓN MÁQUINAS EMPLEADOS
Comments are closed, but trackbacks and pingbacks are open.