CAMPO MAGNÉTICO INDUCCIÓN FÍSICA

BREVE INTRODUCCIÓN DE CAMPO MAGNÉTICO:

Todos hemos tocado y jugado con imanes. Se observa como se atraen, hasta que se quedan unidos, si están colocados en determinada posición uno con respecto al otro. Se observa además que se repelen si se colocan en otra determinada posición. Esto es debido a la existencia de dos «polos» en los imanes. Si se enfrentan «polos» opuestos se atraen y se repelen si se enfrentan polos del mismo tipo. A los polos que presentan los imanes se les han denominado polo Norte y polo Sur.

Esta manifestación es debida a que estos elementos, los imanes, presentan una propiedad que se cuantifica mediante la existencia de un campo que se va a denominar campo magnético.

Los imanes pueden ser naturales (magnetita) o artificiales (se suelen preparar mediante la magnetización del hierro o de algunos metales ferromagnéticos: cobalto (Co), manganeso (Mn), gadolinio (Gd) y disprosio (Dy).

Todos además sabemos ya que la Tierra, debida a múltiples factores (existencia de materiales magnéticos, rotación…) presenta propiedades magnéticas (presenta un campo magnético), que se utilizan de forma notable para la orientación en el planeta mediante la brújula. La brújula no es más que una aguja imantada que se orienta siempre con el campo magnético de la tierra, por lo que señala siempre a un mismo punto cualquiera que sea la posición donde se encuentra, ese punto coincide con el Norte geográfico (Polo Norte), que es el Polo Sur magnético.

Otros aspectos relacionados con el campo mágnetico de gran importancia actual, de un mayor nivel de complejidad, son sus relaciones con las corrientes eléctricas y aquí entraríamos dentro de lo que se conoce como ELECTROMAGNETISMO.

Como ejemplos de esta compleja relación entre las CORRIENTES ELÉCTRICAS y los CAMPOS MAGNÉTICOS tenemos:

la desviación que sufre una aguja imantada (brújula) respecto de su posición normal (la que tiene debida a la presencia del campo magnético terrestre) cuando se la coloca en las proximidades de un conductor por el que circula una corriente eléctrica. Este fenómeno fue ampliamente observado y cuantificado por Christian Oersted (en 1819).
las fuerzas recíprocas que aparecen entre dos conductores cuando pasan por ellos corrientes eléctricas, fenómeno descubierto por Antoine Marie Ampère pocos años después.
mediante la variación de campos magnéticos se pueden inducir corrientes eléctricas. Esta es la propiedad que se utiliza en las centrales eléctricas para producir electricidad (fenómeno de inducción magnética).

En cualquier caso, este es un tema de enorme importancia en física aplicada, ya que el electromagnetismo constituye hoy día el fundamento del poderoso desarrollo tecnológico que vivimos.

CAMPO MAGNÉTICO. INDUCCIÓN MAGNÉTICA:

RECURSOS DE CAMPO MAGNÉTICO PARA FÍSICA DE BACHILLERATO:

APUNTES, RECURSOS DE TEORÍA:

- Fuerza Magnética sobre una carga en movimiento: LEY DE LORENTZ
- Campo Magnético creado por un conductor por el que circula una corriente eléctrica: LEY DE LAPLACE Y DE BIOT Y SAVART
- CAMPO MAGNÉTICO CREADO POR CORRIENTES ELÉCTRICAS: ESPIRA CIRCULAR, SOLENOIDE.
- Fuerza Ejercida por el Campo Magnético sobre un Conductor de Corriente Eléctrica: FUERZA SOBRE UN CONDUCTOR ELÉCTRICO
- TEOREMA DE GAUSS PARA EL CAMPO MAGNÉTICO (SEGUNDA ECUACIÓN DE MAXWELL)

MOVIMIENTO DE UNA PARTÍCULA CARGADA DENTRO DE UN CAMPO MAGNÉTICO UNIFORME:

Lo que se pretende en esta pregunta es obtener la trayectoria de una partícula cargada dentro de un campo magnético uniforme. Para simplificar, nos limitaremos al estudio de la situación en la que la partícula penetra perpendicularmente al campo magnético B con una velocidad v = v_o.

Sabemos que la fuerza a la que se ve sometida una carga en movimiento dentro de un campo magnético uniforme está descrita por la LEY DE LORENTZ, de tal modo que:

Como está definida mediante el producto vectorial, sabemos que la fuerza es perpendicular a v y B. Por ser F perpendicular a v, como F=m·a, la aceleración también es perpendicular a v, en cuyo caso la aceleración sólo tiene componente normal o centrípeta, la componente tangencial es cero (no hay variación del módulo de la velocidad, sólo de la dirección de la velocidad, la partícula lleva un movimiento circular uniforme). Por todo ello:

Como la velocidad es constante y el campo se ha partido de que es uniforme; además estamos viendo el caso en el que la partícula entra perpendicularmente al campo (el ángulo es de 90º)

Esta Fórmula del RADIO, se usa muchísimo en Ejercicios de Campo Magnético.

Notar que el Radio, al ser función de magnitudes todas constantes es también constante, lo que significa que nos encontramos en el caso de movimiento circular.

«Una partícula cargada que penetra en un campo magnético uniforme B con velocidad perpendicular al campo, describe un movimiento circular uniforme.»

En este caso además, pensar que la carga da igual que lleve o no el signo. La presencia de un signo negativo para el radio de un movimiento circular no significa nada.

Ejemplos de esto para una carga positiva y otra negativa:

Se puede además, partiendo de la fórmula anterior, calcular la VELOCIDAD ANGULAR y el PERÍODO del movimiento:

Aplicaciones prácticas del movimiento de una partícula cargada dentro de un campo magnético uniforme tenemos el espectrógrafo de masas y el ciclotrón.

En el ESPECTRÓGRAFO DE MASAS como dependiendo de la masa el radio es diferente, esto nos permite identificar substancias.

El CICLOTRÓN básicamente es un acelerador de partículas, ya que si obligamos a la carga a describir trayectorias de radio cada vez mayor la velocidad será mayor también al ser directamente proporcional al radio.

EJERCICIO F2BE2379:

Un electrón se desplaza con una velocidad: v = 6 j m/s en una zona donde existe un campo magnético uniforme de valor B = 5 i T (Los símbolos en negrita y cursiva indican vector, tanto en la velocidad como en el campo magnético, así como en los vectores unitarios que se indican). En esta situación se pide:

a.- Hallar el vector Fuerza que actúa sobre la carga nombrando la ley que describe este comportamiento.

b.- El movimiento que describe el electrón como consecuencia de la presencia del campo magnético, obteniendo los parámetros característicos del mismo, así como indicando en un dibujo explicativo su trayectoria.

c.- Mencionar brevemente, comparando con los apartados anteriores, lo que ocurriría si en vez de un electrón tuviéramos un protón.

DATO: |q_e-|=|q_p+| = 1.6 · 10^-19C ; m_e-= 9.1 · 10^-31 kg; m_p+= 1.67 · 10^-27 kg.

IR AL VÍDEO QUE RESUELVE EL EJERCICIO : https://youtu.be/WL-Z8eT7jug

EJERCICIO F2BE2380:

En una región del espacio, donde existe un campo magnético orientado hacia arriba, penetra perpendicularmente un protón, con una energía cinética de 6·10^-15 J. Como consecuencia de la situación, el protón describe una trayectoria con un radio de 1,5 cm.

a.- Hallar el valor del campo magnético que genera la situación planteada.

b.- Obtener el valor de la Fuerza a la que se encuentra sometido el protón, al entrar en esta región donde el campo magnético está presente.

c.- Representar la situación, ayudándote de un plano horizontal en el que el protón avanza de izquierda a derecha, dejando clara la trayectoria y dibujando el vector campo magnético, el vector fuerza, el vector velocidad y el vector aceleración, en tres puntos diferentes de la trayectoria.

DATOS: q_p+ = 1.6·10^-19C ; m_p+= 1.67·10^-27 kg.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO : https://youtu.be/R6RXDeNy0io

EJERCICIO F2BE2381:

Mediante una diferencia de potencial de 3000 V, se aceleran iones H⁺ en línea recta. Estos iones penetran en un campo magnético de 0,3 T, perpendicular a la velocidad de los iones. Hallar:

a.- La velocidad con la que los iones penetran en el campo.

b.- El radio de la órbita circular que describen los iones.

c.- El período del movimiento circular que resulta.

DATOS: q_p+ = 1.6·10^-19C ; m_p+= 1.67·10^-27 kg.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/L2KMyJzTlVo

EJERCICIO F2BE2382:

Un electrón entra perpendicularmente en un campo magnético uniforme de 0,25 T. La velocidad con la que entra la obtuvo aplicándole una diferencia de potencial de 2000 V. Hallar:

a.- La velocidad que adquiere el electrón, como consecuencia de la diferencia de potencial aplicada.

b.- La fuerza a la que se verá sometido el electrón una vez entra en el campo magnético, explicando en un diagrama la dirección y sentido de la misma.

c.- Explicar, argumentando con rigor, la trayectoria que sigue, obteniendo el radio de la misma.

d.- Hallar el periodo del movimiento que resulta cuando el electrón está afectado por el campo magnético.

e.- Realizar un dibujo explicativo, con el rigor esperado en este nivel en el que se observe el electrón entrando horizontalmente de izquierda a derecha y encontrándose con el campo magnético perpendicular y hacia arriba, que incluya en él:

El dibujo de la trayectoria que sigue el electrón.

El vector fuerza al que se encuentra sometido, el vector velocidad y el vector aceleración (los tres vectores en dos puntos de la trayectoria)

f.- Hallar la masa relativista del electrón, comparando con la masa en reposo del electrón, añadiendo comentarios a las diferencias observadas, tomando como base argumentativa la Teoría de la Relatividad.

DATOS: c=3·10⁸ m/s; m_e-= 9,1·10^-31 kg; |q_e-|=1,6·10^-19 C.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/hhGiCWoFHgA

EJERCICIO F2BE2692:

Suponiendo que un electrón se mueve de izquierda a derecha a lo largo de una línea horizontal en el plano del papel y que se encuentra con un campo magnético perpendicular al plano del papel de valor 10 ^{– 2} T según el esquema adjunto.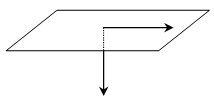

a.- Hallar el radio de la trayectoria si la velocidad la ha alcanzado acelerando el electrón desde el reposo con una diferencia de potencial de 1000 V.

b.- Dibujar la trayectoria del electrón. Indicar la fuerza magnética, la aceleración del movimiento y la velocidad en dos puntos de la trayectoria.

c.- Indicar como varía la energía cinética del electrón a lo largo de su movimiento con todo lujo de detalles y argumentación.

DATOS: q_e= – 1.6 × 10⁻¹⁹ C ; m_e= 9.11 × 10⁻³¹ kg

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ELECTROMAGNETISMO

EJERCICIO F2BE2455:

Un electrón entra con una velocidad v=5·10⁴ i * (m/s) en una región del espacio donde hay un campo magnético uniforme B=-2,5 j * (T). Para el instante de entrada, determine:

*Con negrita queremos indicar vector.

a) La fuerza que ejerce el campo magnético sobre el electrón y el vector aceleración

b) El radio de la trayectoria que describe el electrón al moverse en interior del campo. Dibuje la trayectoria, el vector campo magnético, así como su velocidad y aceleración en un punto arbitrario de la trayectoria

c) La energía cinética y el tiempo que tarda en dar una vuelta completa.

Datos: q_e= -1,6 ×10⁻¹⁹ C ; m_e= 9,11×10⁻³¹ kg

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO Y OTROS DE INTERÉS PARA FÍSICA DE 2º DE BACHILLERATO: PRUEBA DE EXAMEN FÍSICA 2º BACHILLERATO. GRAVITATORIO, ELÉCTRICO, MAGNÉTICO, ONDAS

CUESTIÓN F2BE2460:

¿Cuál es la expresión de la fuerza que actúa sobre un electrón de velocidad v, que penetra en una región del espacio donde se aplica un campo magnético uniforme B? ¿En qué situación el campo magnético presente no influirá en el movimiento del electrón?

EJERCICIO F2BE2925:

Hallar el vector fuerza magnética que sufrirá la partícula correspondiente en presencia del campo magnético indicado y moviéndose a la velocidad que se muestra, en los siguientes casos, donde los vectores se consideran según el sistema cartesiano habitual (XYZ), y las magnitudes se suponen en unidades del S.I.:

DATOS: |q_e-|=|q_p+| = 1.6 · 10^-19C

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO PARA FÍSICA DE 2º DE BACHILLERATO. MOVIMIENTO ARMÓNICO SIMPLE, GRAVITACIÓN Y ELECTROMAGNETISMO. SEGUNDO TRIMESTRE CURSO 2024-25

EJERCICIO F2BE2978:

DATOS: |q_e-|=|q_p+| = 1.6 · 10^-19C

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE FÍSICA 2º BACHILLERATO: ONDAS, EFECTO DOPPLER, ELECTROMAGNETISMO Y GRAVITACIÓN. CURSO 2024-25.

EJERCICIO F2BE2857:

Mediante una diferencia de potencial de 2575 V, se aceleran electrones, de tal manera que llevan la dirección del eje OX negativo. Si sabemos que en la zona existe un campo magnético de 0,4 T en la dirección del eje OZ, sentido positivo.

a.- Hallar la velocidad, vector y módulo con la que el electrón entra en el campo magnético.

b.- Hallar la fuerza magnética a la que se verá sometido el electrón, vector y módulo. Realizar este apartado de dos maneras diferentes.

c.- Hallar el radio del movimiento que resulta y la velocidad angular, en unidades del S.I. y en r.p.m.

d.- Hallar el periodo del movimiento que resulta.

e.- Hallar la energía cinética del electrón una vez han pasado 3 ms desde que se introduce en el campo magnético.

f.- Hallar la aceleración que sufre el electrón.

g.- Realizar un esquema claro y con rigor de la situación planteada, donde se observe la velocidad, la fuerza, la aceleración en dos puntos distintos de la trayectoria.

h.- Indicar el plano en el que se encuentra la trayectoria, el plano del movimiento.

i.- Realizar el ejercicio nuevamente si fuera un protón y si fuera un neutrón.

j.- Obtener las unidades de la constante magnética en el vacío, utilizando alguna fórmula apropiada.

DATOS: q_p+ = 1.6·10^-19C ; m_p+= 1.67·10^-27 kg; m_n=1,67·10^-27; m_e=9,11·10^-31 kg; µ₀= 4π·10-7 u.S.I.

EJERCICIO F2BE2863 ≈ F2BE2857:

Mediante una diferencia de potencial de 2600 V, se aceleran electrones, de tal manera que llevan la dirección del eje OY negativo. Si sabemos que en la zona existe un campo magnético de 0,3 T en la dirección del eje OX, sentido positivo.

a.- Hallar la velocidad, vector y módulo con la que el electrón entra en el campo magnético.

b.- Hallar la fuerza magnética a la que se verá sometido el electrón en el instante inicial, vector y módulo. Realizar este apartado de dos maneras diferentes y nombrar la Ley que se utiliza.

c.- Hallar el radio del movimiento que resulta y la velocidad angular, en unidades del S.I. y en r.p.m.

d.- Hallar el periodo del movimiento que resulta.

e.- Hallar la energía cinética del electrón una vez han pasado 3 s desde que se introduce en el campo magnético.

f.- Hallar la energía potencial del electrón sometido al campo magnético, indicando el modo en que varía.

g.- Hallar el módulo de la aceleración que sufre el electrón.

h.- Realizar un esquema claro y con rigor de la situación planteada, donde se observe la velocidad, la fuerza, la aceleración en dos puntos distintos de la trayectoria, así como el giro del electrón en la misma.

i.- Indicar el plano en el que se encuentra la trayectoria, esto es el plano donde se desarrolla el movimiento.

j.- Hallar la fuerza magnética (vector y módulo) que se obtendría si fuera un protón.

k.- Hallar la fuerza magnética (vector y módulo) que se obtendría si fuera un neutrón.

l.- Obtener las unidades de la constante magnética µ₀, utilizando alguna expresión / fórmula apropiada, que debe nombrarse e indicar su utilidad.

m.- Con la misma velocidad obtenida en el apartado a, hallar la fuerza magnética que sufriría el electrón si el vector campo magnético fuera el vector B = 0,3 j (con negrita queremos indicar vector).

DATOS: q_p+ = 1.6·10^-19C ; q_e- = – 1.6·10^-19C ; m_p+= 1.67·10^-27 kg; m_n=1,67·10^-27; m_e=9,11·10^-31 kg; µ₀= 4π·10^-7 u.S.I.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EJERCICIO RESUELTO DE CAMPO MAGNÉTICO, ELECTROMAGNETISMO, CORRESPONDIENTE A TRABAJO TRIMESTRAL PARA FÍSICA DE 2º DE BACHILLERATO.

CUESTIÓN F2BE2897, (B5 JULIO 2020 CANARIAS):

Un protón que se mueve con velocidad constante en el sentido positivo del eje X penetra en una región del espacio donde hay un campo eléctrico E = – 3,5·10⁵ i (N/C)* y un campo magnético B = 2j (T)*. Determine el módulo de la velocidad que debe llevar el protón al penetrar en la región para que la atraviese a velocidad constante, sin ser desviado.

*con negrita queremos indicar vector

IR A LA RESOLUCIÓN PASO A PASO DE ESTA CUESTIÓN, ALGO CONFUSA: CUESTIÓN RESUELTA ELECTROMAGNETISMO. EBAU CANARIAS JULIO 2020. FÍSICA 2º BACHILLERATO

CUESTIÓN F2BE2899,:

Un protón que se mueve con velocidad indeterminada penetra en una región del espacio donde hay un campo eléctrico E = – 3,5·10⁵ i (N/C)* y un campo magnético B = 2j (T)*. Determine el módulo, dirección y sentido de la velocidad que debe llevar el protón al penetrar en la región para que la atraviese a velocidad constante, sin ser desviado.

*con negrita queremos indicar vector

EJERCICIO F2BE2874:

Mediante una diferencia de potencial de 1500 V, se aceleran protones, de tal manera que llevan la dirección del eje OY positivo. Si sabemos que en la zona existe un campo magnético de 0,25 T en la dirección del eje OX, sentido negativo, responder a las siguientes cuestiones:

a.- Hallar la fuerza magnética a la que se verá sometido el protón en el instante inicial, vector y módulo. Realizar este apartado de dos maneras diferentes y nombrar la Ley que se utiliza.

b.- Hallar la velocidad angular del protón, en unidades del S.I. y en r.p.m., justificando que el movimiento del protón como consecuencia de la situación planteada es circular y uniforme.

DATOS: q_p+ = 1.6·10^-19C ; m_p+= 1.67·10^-27 kg; µ₀= 4π·10^-7 u.S.I.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE CAMPO MAGNÉTICO: EXAMEN RESUELTO CON EJERCICIOS DE CAMPOS GRAVITATORIO, ELECTROSTÁTICO Y MAGNÉTICO, CORRESPONDIENTE A PRUEBA FINAL PRIMER TRIMESTRE 2024-25, PARA FÍSICA DE 2º DE BACHILLERATO

ACCIONES ENTRE CORRIENTES PARALELAS E INDEFINIDAS; DEFINICIÓN DE AMPERIO. FUERZAS ENTRE CORRIENTES:

Una carga en movimiento, se verá afectada por la presencia de un campo magnético, de tal manera que sobre ella aparece una fuerza magnética que define la Ley de Lorentz. Con más motivo entonces, una corriente eléctrica, que no es sino un chorro de electrones, cargas todos ellos en movimiento, se verá afectada por un campo magnético. Para complicar las cosas, una corriente eléctrica perturba el medio que le rodea, creando un campo magnético, que define, si el conductor es rectilíneo la Ley de Biot-Savart. Es por ello que se producen acciones entre dos corrientes; en nuestro caso vamos a ver ejemplos de corrientes paralelas y rectilíneas.

Distinguiremos dos casos, en A) por los conductores rectilíneos y paralelos circulan corrientes en el mismo sentido, en B) en sentidos contrarios.

CASO A): CORRIENTES EN EL MISMO SENTIDO:

El conductor 1, crea en el punto O₂ (del conductor 2) un campo magnético, B₁ cuyo valor es por la Ley de Biot y Savart:

La dirección y sentido de B₁ es la que aparece en el dibujo A.

Como este campo magnético (B₁), afecta al conductor de corriente(2), sobre este conductor, aparece una fuerza F_1-2 de valor en módulo:

La dirección y sentido de F_1-2 es la que aparece en el dibujo, según la regla de la mano derecha, para este producto vectorial.

Del mismo modo, el conductor 2, crea en el punto O₁ (del conductor 1) un campo magnético, B₂ cuyo valor es por La Ley de Biot y Savart:

La dirección y sentido de B₂ es la que aparece en el dibujo A.

Como este campo magnético (B₂), afecta al conductor de corriente(1), sobre este conductor, aparece una fuerza F_2-1 de valor en módulo:

La dirección y sentido de F_2-1 es la que aparece en el dibujo, según la regla de la mano derecha, para este producto vectorial.

Notar que en módulos: F_2-1 = F_1-2 , que sólo varían en el sentido.

CASO B) CORRIENTES EN SENTIDO CONTRARIO:

Los módulos de las fuerzas implicadas son también los mismos lo único que varían es el sentido, ya que al invertirse el sentido de la corriente en el conductor 2, se invierte también el sentido de la fuerza como se observa en el dibujo del caso B).

En conclusión, dos corrientes rectilíneas y paralelas del mismo sentido se atraen y de sentido contrario se repelen tal como hemos visto obteniendo las fuerzas.

Lo más importante de lo que estamos comentando es caer en la cuenta de cómo se combinan los dos efectos electromagnéticos más importantes que hemos visto. Por un lado, las corrientes eléctricas perturban las propiedades del medio en el sentido que crean a su alrededor un campo magnético; y por otro lado cuando tenemos un conductor en una zona en la que existe un campo magnético, si por él circula una corriente eléctrica, aparece una fuerza.

Estos dos efectos combinados son lo que produce que dos corrientes del mismo sentido se atraen y de sentido contrario se repelen.

DEFINICIÓN DE AMPERIO:

Partiendo de:

Que es la fuerza por unidad de longitud con la que se atraen o repelen dos conductores por los que circulan corrientes, la 11 Conferencia General de Pesas y Medidas decidió en 1960, adoptar el amperio (A) como unidad fundamental del SI de unidades, que se define como:

«Amperio es la intensidad de corriente que: circulando por dos conductores rectilíneos y paralelos de longitud indefinida y sección despreciable, puesto en el vacío a la distancia de un metro, produce en cada conductor una fuerza de 2·10^-7 N por metro de longitud».

CUESTIÓN F2BE2667 (EBAU CANARIAS JULIO 23):

Se tienen dos hilos conductores rectilíneos, indefinidos, paralelos entre sí, separados 50 cm, por los que circulan dos corrientes en sentidos opuestos de I₁= 2 A e I₂ = 5 A.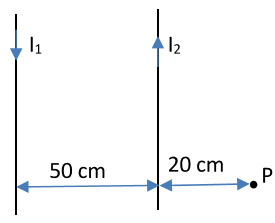

Calcular la intensidad del campo magnético en el punto P.

DATO: μ₀=4π·10^-7 N·A^-2

AMPLIACIÓN: PROPONER UN SISTEMA DE REFERENCIA EN TRES DIMENSIONES COHERENTE CON LA SITUACIÓN Y UTILIZARLO PARA INDICAR CORRECTAMENTE EL VECTOR CAMPO MAGNÉTICO EN P

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA CUESTIÓN DE CAMPO MAGNÉTICO: EXAMEN RESUELTO FÍSICA EBAU CANARIAS 2023. CONVOCATORIA EXTRAORDINARIA JULIO

EJERCICIO F2BE2383:

Disponemos de 3 conductores rectilíneos, paralelos y largos separados 10 cm entre sí, por los que circulan corrientes de 5 A, según los sentidos que se indican en el esquema siguiente:

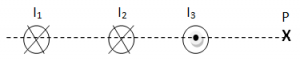
a.- Obtener el campo magnético que se crea en el punto P (a 15 cm del conductor I₃) como consecuencia de la presencia de las tres corrientes indicadas, dibujando el campo magnético resultante, así como cada uno de los campos magnéticos parciales.

RESOLUCIÓN DE ESTE PRIMER APARTADO DEL EJERCICIO A TRAVÉS DEL VÍDEO: https://youtu.be/fneTQGlqq_Y

b.- Hallar la fuerza por unidad de longitud que se produce en el segundo conductor como consecuencia de la presencia de los otros dos, dibujándola, así como todo lo necesario en el proceso.

DATOS: µ₀=4π·10^-7 N·A²

RESOLUCIÓN DE ESTE SEGUNDO APARTADO DEL EJERCICIO : https://youtu.be/WWViDmt9iQk

EJERCICIO F2BE2388:

Disponemos de 3 conductores rectilíneos y largos colocados según se indica en el diagrama, con los sentidos de la corriente igualmente señalados. Las intensidades (I₁=3 A, I₂=5 A, I₃=7 A).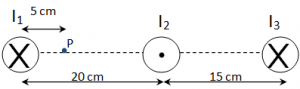

Hallar el valor del campo magnético resultante en el punto P ( a 5 cm del conductor 1) indicando la dirección y el sentido de este campo resultante, así como de los campos parciales.

DATO: μ₀=4π·10^-7 T·m/A

SOLUCIÓN: 1,4·10^-5 T (perpendicular a la línea que une los conductores y hacia abajo)

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ELECTROMAGNETISMO Y ÓPTICA. SEGUNDA PRUEBA DEL SEGUNDO TRIMESTRE DEL CURSO 2024-25

EJERCICIO F2BE2456:

Dos conductores rectos y paralelos están separados por una distancia de 20 cm y están recorridos en el mismo sentido por sendas intensidades de la corriente eléctrica de 5 A y 20 A. ¿A qué distancia de los conductores se anula el campo magnético? ¿Cuánto vale el campo magnético en un punto situado 5 cm a la izquierda del primer conductor?

Dato: µ₀ = 4π ⋅ 10^-7 Tm/A

EJERCICIO F2BE2389:

En un sistema de referencia cartesiano en 3 dimensiones, un electrón se mueve con una velocidad de 2 m/s en la dirección negativa del eje OY, existiendo en la zona un campo magnético uniforme de 3 T en la dirección positiva del eje OX. En esta situación se pide:

a.- Obtener el vector fuerza magnética al que se verá sometido el electrón, dibujando claramente en el sistema de referencia los vectores implicados, así como el vector fuerza magnética.

b.- Hallar el radio* de la trayectoria del movimiento del electrón, indicando en el sistema de referencia la trayectoria.

*obtener la expresión del radio con rigor, partiendo de las leyes correspondientes y haciendo e indicando las suposiciones y argumentaciones necesarias.

c.- Hallar el periodo del movimiento que resulta.

DATOS: m_e-= 9,1·10^-31 kg; |q_e-|=1,6·10^-19 C.

SOLUCIONES: -9,6·10-19 k (N); 3,79·10^-11 m; 1,19·10^-11 s

EJERCICIO F2BE2532:

Un electrón entra perpendicularmente en un campo magnético uniforme de 0,3 T. La velocidad con la que entra en el sentido positivo del eje OX del sistema de referencia cartesiano habitual, la obtuvo aplicándole una diferencia de potencial de 5000 V. El campo magnético está dirigido en el sentido negativo del eje OZ. Hallar:

a.- La fuerza a la que se verá sometido el electrón una vez entra en el campo magnético, explicando en un diagrama la dirección y sentido de la misma.

b.- Explicar, argumentando con rigor, la trayectoria que sigue, obteniendo el radio de la misma y el periodo si fuera posible.

c.- Realizar un dibujo explicativo, con el rigor esperado en este nivel en el que se observe el electrón entrando horizontalmente y encontrándose con el campo magnético, que incluya en él: el dibujo de la trayectoria que sigue el electrón; el vector fuerza al que se encuentra sometido, el vector velocidad y el vector aceleración (los tres vectores en dos puntos diferentes de la trayectoria)

d.- Hallar la masa relativista del electrón, comparando con la masa en reposo del electrón, añadiendo comentarios a las diferencias observadas, tomando como base argumentativa la Teoría de la Relatividad.

DATOS: c=3·10⁸ m/s; m_e-= 9,1·10^-31 kg; |q_e-|=1,6·10^-19 C.

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO Y OTROS DE INTERÉS PARA FÍSICA DE 2º DE BACHILLERATO: EXAMEN RESUELTO DE FÍSICA DE 2º DE BACHILLERATO: CAMPO ELECTROSTÁTICO, MAGNÉTICO, ONDAS, RELATIVIDAD, CUÁNTICA, ÓPTICA Y DEFECTOS DEL OJO.

EJERCICIO F2BE2396 (X871):

Por el cable 1 circula una corriente de I₁=3 A, en el sentido indicado (perpendicular al plano del papel y hacia dentro, según la simbología habitual); por el cable 2 una corriente de I₂=4,5 A, en el sentido indicado (perpendicular al plano del papel y hacia afuera). Las distancias de cada cable de corriente al punto P están indicadas en el dibujo.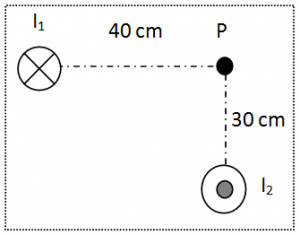

Suponiendo que los cables son rectilíneos e indefinidos, hallar:

a.- El vector campo magnético (B) que se genera en el punto P, como consecuencia de la presencia de los dos cables, situando el sistema de referencia cartesiano XY habitual en el punto P, que debe indicarse en el dibujo, así como los campos magnéticos parciales.

b.- El módulo del campo magnético en P.

c.- Dibujar el campo magnético que el conductor 1 crea en el conductor 2, obteniendo su módulo.

d.- Hallar la fuerza que el conductor 1, produce sobre el conductor 2 por unidad de longitud, calculando su módulo e indicando en el dibujo la dirección y el sentido de la fuerza.

DATOS: µ₀=4π·10^-7 T·m/A

SOLUCIONES: B_P=-3·10^-6 i – 1,5·10^-6 j (T); B=5,58·10^-6 T; B₁=1,2·10^-6 T; F/L=5,4·10^-6 N/m

EJERCICIO F2BE2617 (X803):

Se acelera un electrón como consecuencia de aplicarle una diferencia de potencial de 250 V, de tal manera que se introduce en un campo magnético uniforme a lo largo del eje OX (sistema de referencia cartesiano en 3D habitual), notándose que en esta situación, no actúa ninguna fuerza sobre la carga. Cuando la carga se mueve a la misma velocidad, pero en la direccción positiva del eje OY, la fuerza ejercida sobre la carga es de 3,2·10^-8 dinas, estando dirigida dicha fuerza en el sentido positivo del eje OZ. Determinar el vector inducción B, indicando módulo, dirección y sentido, así como sus componentes vectoriales con rigor.

DATOS: |q_electrón| = 1.6·10^-19 C; m_electrón= 9.11·10^-31 kg; 1 dina = 10^-5 N.

SOLUCIÓN: B=0,21 i (T)

EJERCICIO F2BE2666:

Un electrón entra con una velocidad v = 2,3·10⁴ j * (m/s) en una región del espacio donde hay un campo magnético uniforme B = – 2,5 k * (T). Para el instante de entrada, determine:

*Con negrita queremos indicar vector.

a) Dibujar en un diagrama cartesiano los vectores velocidad, campo magnético así como el vector fuerza que aparece como consecuencia de la situación planteada.

b) La fuerza que ejerce el campo magnético sobre el electrón (vector y módulo).

c) La aceleración a la que se verá sometido el electrón (vector y módulo).

d) El radio de la trayectoria que describe el electrón al moverse en interior del campo.

e) La energía cinética que lleva el electrón antes de encontrarse con el campo magnético.

f) La energía cinética que adquiere el electrón una vez se ha encontrado sometido al campo magnético.

g) Indicar razonadamente y con rigor el modo en que varía la energía cinética del electrón mientras se encuentra sometido a la situación planteada.

h) Hallar el período del movimiento del electrón.

i) Hallar el tiempo que tarda en realizar un millón de vueltas completas.

j) Dibuje la trayectoria, el vector campo magnético, así como su velocidad y aceleración en dos puntos arbitrarios de la trayectoria

k) Hallar el vector fuerza, el vector aceleración, el radio de la trayectoria y el período del movimiento, en el caso que la partícula que entra en el campo magnético sea un protón.

l) Hallar el vector fuerza, el vector aceleración, el radio de la trayectoria y el período del movimiento, en el caso que la partícula que entra en el campo magnético sea un neutrón.

Datos: q_e= -1,6 ×10⁻¹⁹ C ; m_e= 9,11×10⁻³¹ kg ; q_p= +1,6 ×10⁻¹⁹ C ; m_p= 1,6726×10⁻²⁷ kg ; m_n= 1,6749×10⁻²⁷ kg

EJERCICIO F2BE2675: (ACTIVIDAD INTERDEPARTAMENTAL INTEGRALES).

Se ha diseñado un nuevo dispositivo que produce campos magnéticos variables en función del tiempo. El problema del dispositivo es que de la función B(t) que define el comportamiento del campo variable, sólo se conoce su derivada, es decir, se sabe que B'(t)=3 t, donde B se mide en Teslas y t en segundos.

Después de un estudio exhaustivo del dispositivo se ha conseguido saber que el campo magnético a los dos segundos de iniciar la experiencia es de 6 Tesla y que hay que introducir una medida de seguridad, ya que si no alcanzaría un valor de 5401 T cuando ha pasado un minuto, valores que son dañinos para la salud y el entorno.

Por ello se ha manipulado el aparato para que a partir de 10 segundos el campo magnético se mantenga constante.

Se ha conectado el dispositivo y se ha introducido un electrón en el área de influencia del que se ha acelerado mediante una diferencia de potencial de 1000 V, justo en el instante t=4 s, moviéndose el electrón en la dirección negativa del eje OZ perpendicular al campo magnético que se dirige en la dirección positiva del eje OY.

Para la situación descrita, responder a las siguientes cuestiones:

a.- Hallar la expresión del campo magnético en función del tiempo B(t), incluyendo la medida de seguridad introducida, con todo el rigor matemático posible, utilizando una expresión analítica para la función, extremadamente correcta. (1,5 p)

b.- Hallar la velocidad con la que se introduce el electrón en el campo magnético descrito. (1,5 p)

c.- Hallar el valor de la fuerza magnética a la que se verá sometido el electrón (vector y módulo) según el S.R. mencionado, utilizando dos maneras: la del determinante que calcula el producto vectorial y utilizando la geometría con la regla de la mano derecha o similar. (3 p)

d.- Explicar razonadamente la trayectoria que describirá el electrón y la razón por la que la describe. (1 p)

e.- Hallar el radio y el período del movimiento del electrón, obteniendo en la medida de lo posible las expresiones que se utilicen para el cálculo de lo que se solicita. (2 p)

f.- Realizar un dibujo-esquema de la situación donde se observen los vectores velocidad y campo magnético. Indicar además la trayectoria y sobre ella y en dos puntos de la misma indicar la velocidad, la aceleración y la fuerza magnética. (1 p)

DATOS: |q_e-|=|q_p+| = 1.6 · 10^-19C ; m_e-= 9.1 · 10^-31 kg; m_p+= 1.67 · 10^-27 kg.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE CAMPO MAGNÉTICO, RELACIONADO CON LA UTILIZACIÓN DE LAS INTEGRALES.

EJERCICIO F2BE2677:

Un electrón que se mueve en la dirección negativa del eje OZ con una velocidad de 1,88·10⁷ m/s se encuentra con un campo magnético de 150 T en la dirección positiva del eje OY. Para la situación descrita:

d.- Explicar razonadamente la trayectoria que describirá el electrón y la razón por la que la describe. (1 p)

e.- Hallar el radio y el período del movimiento del electrón, obteniendo en la medida de lo posible las expresiones que se utilicen para el cálculo de lo que se solicita. (2 p)

DATOS: |q_e-|=|q_p+| = 1.6 · 10^-19C ; m_e-= 9.1 · 10^-31 kg; m_p+= 1.67 · 10^-27 kg.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE CAMPO MAGNÉTICO, RELACIONADO CON LA UTILIZACIÓN DE LAS INTEGRALES.

CUESTIÓN F2BE2705, EBAU CANARIAS JUNIO 2022:

En una región del espacio se aplica un campo magnético de 1,5 T. Si se lanza un protón perpendicularmente a las líneas de campo a la velocidad de 1,8·106 m/s, calcule la fuerza magnética que actúa sobre el protón y el radio de la circunferencia que describe.

Datos: m_p=1.67·10^-27 kg; q_p=1.6·10^-19 C

IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE FÍSICA DE 2º DE BACHILLERATO: GRAVITACIÓN, ELECTROMAGNETISMO Y ECUACIÓN DE ONDAS

CUESTIÓN F2BE2468:

Selector de velocidades. Diagrama y en qué consiste.

RELACIONES DEL CAMPO MAGNÉTICO CON EL CAMPO ELÉCTRICO:

ANALOGÍAS Y DIFERENCIAS ENTRE CAMPOS ELÉCTRICO Y MAGNÉTICO

EJERCICIOS DE CAMPO MAGNÉTICO: CON SOLUCIÓN Y CON LA RESOLUCIÓN PASO A PASO:

Ejercicios de interacción electromagnética, con la solución (136, 135): EJERCICIOS CAMPO MAGNÉTICO
Ejercicios de Campo Magnético RESUELTOS: EJERCICIOS CAMPO MAGNÉTICO RESUELTOS PASO A PASO
Ejercicios de Campo Magnético con la Solución: EJERCICIOS CON SOLUCIÓN DE CAMPO MAGNÉTICO
Cuestiones de Campo Magnético: CUESTIONES CAMPO MAGNÉTICO

INDUCCIÓN MAGNÉTICA:

EJERCICIO F2BE3008:

Indicar partiendo de la ley correspondiente (que debe nombrarse y formularse) lo que tiene que ocurrir para que se produzca una fuerza electromotriz inducida.

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE ELECTROMAGNETISMO Y ÓPTICA. TERCERA PRUEBA DEL SEGUNDO TRIMESTRE DEL CURSO 2024-25

EJERCICIO F2BE3009-F2BE2425:

Una bobina de 50 espiras circulares de 10 cm de diámetro se sitúa perpendicularmente a un campo magnético variable cuyo módulo en función del tiempo es B(t)=0,5·sen(t²/2π), en unidades del S.I.. Obtener la expresión en función del tiempo del flujo de campo magnético y de la fuerza electromotriz inducida en la bobina.

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE ELECTROMAGNETISMO Y ÓPTICA. TERCERA PRUEBA DEL SEGUNDO TRIMESTRE DEL CURSO 2024-25

EJERCICIO F2BE3104:

Disponemos de 2 conductores rectilíneos, según el siguiente esquema, paralelos y largos separados 15 cm entre sí, por los que circulan corrientes de I₁=6 A e I₂=14 A, según los sentidos que se indican en el esquema siguiente:

a.- Obtener el campo magnético que se crea en el punto P (a 5 cm del conductor I₂) como consecuencia de la presencia de las dos corrientes indicadas, dibujando el campo magnético resultante, así como cada uno de los campos magnéticos parciales.

b.- Hallar el punto exacto en la línea que une a los dos conductores en el que el campo magnético se anula, razonando con rigor el proceso.

DATOS: µ₀=4π·10^-7 N·A²

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE FÍSICA DE 2º BACHILLERATO. TERCER TRIMESTRE DEL CURSO 2024-25

JERCICIO F2BE3105:

a.- Enunciar y formular la Ley de Faraday-Henry-Lenz de inducción magnética, haciendo comentarios a lo que debe ocurrir para que se produzca una corriente inducida.

SOLUCIÓN DE ESTE APARTADO:

Para que se produzca una fuerza electromotriz inducida, tiene que producirse una variación del flujo de campo magnético que atraviesa una determinada superficie. Tal realidad se contempla en la Ley de Faraday-Henry-Lenz.

Para que varíe el flujo de campo magnético, tiene que variar el campo magnético, la superficie de la espira o el ángulo que forman.

Más información al respecto en: LEY DE FARADAY DE INDUCCIÓN MAGNÉTICA: LEY DE FARADAY-HENRY-LENZ.

b.- De una corriente inducida se conoce en un determinado intervalo de tiempo que la fuerza electromotriz inducida responde, en función del tiempo a la siguiente expresión, en unidades del S.I.: e(t) = 4t². Obtener el flujo de campo magnético en función del tiempo, cuya variación la produce, sabiendo que en el instante t=1 s, el flujo es de 1,5 wb.

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE FÍSICA DE 2º BACHILLERATO. TERCER TRIMESTRE DEL CURSO 2024-25

Post Views: 3.141