REGLA DE TRES INVERSA
PODRÍA INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
SIGUE EL PROCESO DETERMINADO POR:
Es el método más sencillo y usado para calcular una cantidad que forma proporción con otras tres cantidades conocidas de magnitudes que son inversamente proporcionales. La manera de resolver la regla de tres en este caso es EN LÍNEA, a diferencia de la REGLA DE TRES DIRECTA, que es en cruz.
Dos magnitudes son inversamente proporcionales si al multiplicar o dividir uno de los valores de una magnitud por un número, el valor correspondiente de la otra magnitud queda dividida o multiplicada por ese número.
De manera más sencilla: si al aumentar una de ellas, la otra también disminuye o a la inversa, caso contrario a las magnitudes directamente proporcionales.
EJERCICIO M1EE3297:
Cuatro pintores tardan 12 días en pintar un muro. Si queremos terminar de pintarlo en 8 días, ¿cuántos pintores necesitaremos?
RESPUESTA:
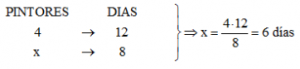
Se ve claramente que se trata de dos magnitudes inversamente proporcionales (al aumentar el número de pintores disminuye el número de días que tardamos en pintar el muro).
Como se puede observar hemos multiplicado «EN LÍNEA» para obtener la x, a diferencia de la regla de tres directa que es «en cruz».
EJERCICIOS CON SOLUCIÓN DE APLICACIÓN DE LA REGLA DE TRES INVERSA:
EJERCICIO M2EE1757:
Cinco carpinteros necesitan 21 días para entarimar un suelo. ¿Cuántos carpinteros serán necesarios si se desea hacer el trabajo en 15 días?
SOLUCIÓN: 7 carpinteros
EJERCICIO M2EE1759:
Un campamento de refugiados que alberga a 4 600 personas tiene víveres para 24 semanas. ¿En cuánto se reducirá ese tiempo con la llegada de 200 nuevos refugiados?
SOLUCIÓN: 1 semana
EJERCICIO M2EE1760:
Una finca tiene una valla antigua sostenida por 650 postes que están colocados a intervalos de 1,20 m. ¿Cuántos postes se necesitarán para la nueva valla en la que los postes se colocarán a intervalos de 1,30 m?
SOLUCIÓN: 600 postes
EJERCICIO M2EE1763:
Una locomotora, a 85 km/h, tarda tres horas y dieciocho minutos en realizar el viaje de ida entre dos ciudades. ¿Cuánto tardará en el viaje de vuelta si aumenta su velocidad a 110 km/h?
SOLUCIÓN: 2 horas, 33 minutos


