CHOQUES ELÁSTICOS COEFICIENTE RESTITUCIÓN
CHOQUES ELÁSTICOS E INELÁSTICOS. COEFICIENTE DE RESTITUCIÓN:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
-
- CANTIDAD DE MOVIMIENTO O MOMENTO LINEAL, IMPULSO. TEOREMA DE CONSERVACIÓN. EJERCICIOS RESUELTOS
- LEYES DE NEWTON
- DINÁMICA Y CINEMÁTICA PARA FÍSICA DE SECUNDARIA. LEYES DE NEWTON
- UTILIZACIÓN DE LAS LEYES DE NEWTON EN EJERCICIOS DE DINÁMICA. FÍSICA DE SECUNDARIA Y BACHILLERATO
- PROFUNDIZANDO EN LAS LEYES DE NEWTON
Sabemos que en los choques elásticos se conserva la energía cinética. Esto nos proporciona otra ecuación que junto con la de la conservación de la cantidad de movimiento nos permite resolver el problema.
En los choques completamente inelásticos o plásticos, en el que las partículas quedan unidas tras la colisión, basta con la conservación de la cantidad de movimiento, pues en este caso:
![]()
Ecuación que nos permite conocer la velocidad tras el choque.
En todos los demás casos debemos conocer qué pérdida de energía se produce durante el choque. Para ello se introduce el COEFICIENTE DE RESTITUCIÓN, definido como:
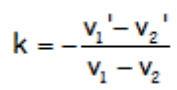
Su valor está comprendido entre 0 y 1, correspondiendo el valor 1 al choque elástico y el valor 0 al choque totalmente inelástico o plástico.
EJERCICIO FQ1BE1418:
Una pelota de 300 g de masa se deja caer desde una altura de 4 m. Después de chocar contra el suelo, se eleva hasta una altura de 2 m. Calcular el coeficiente de restitución del choque.
RESOLUCIÓN DEL EJERCICIO:
El coeficiente de restitución, teniendo en cuenta que para el suelo, tanto la velocidad antes como después del choque es cero: (los subíndices 2 para el suelo, y 1 para la pelota)
v1 , la velocidad de la pelota antes del choque, la obtendremos por conservación de la energía mecánica, considerando la posición inicial en la que la soltamos desde una altura de 4 m y la final en la que toca con el suelo:
v1 ‘, la velocidad de la pelota después del choque, la obtendremos igual, considerando la posición inicial en la que la sale despedida del suelo y la final en la que se para a una altura de 2m:
Teniendo en cuenta que tienen sentidos diferentes:


