DISTANCIAS PUNTOS RECTAS PLANOS
DISTANCIAS ENTRE PUNTOS, RECTAS Y PLANOS. GEOMETRÍA MÉTRICA EN EL ESPACIO. EJERCICIOS RESUELTOS:

PODRÍA INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
-
- GEOMETRÍA PLANA PARA SECUNDARIA Y 1º DE BACHILLERATO
- GEOMETRÍA ESPACIAL PARA BACHILLERATO
- GEOMETRÍA ESPACIAL. ECUACIONES DE LA RECTA EN 3 DIMENSIONES
- POSICIONES RELATIVAS DE DOS RECTAS EN EL ESPACIO, PARA MATEMÁTICAS II DE 2º BACHILLERATO
- GEOMETRÍA ESPACIAL. ECUACIONES DEL PLANO EN TRES DIMENSIONES
- CONDICIÓN DE PUNTOS ALINEADOS. GEOMETRÍA ESPACIAL PARA BACHILLERATO. EJERCICIOS RESUELTOS
- CONDICIÓN DE PUNTOS COPLANARIOS. GEOMETRÍA ESPACIAL PARA BACHILLERATO. EJERCICIOS RESUELTOS
FORMA PARTE DE LOS MATERIALES DE LA PROGRAMACIÓN DIDÁCTICA:
DISTANCIA ENTRE DOS PUNTOS:
La distancia entre dos puntos A y B es el módulo del vector que los une. Se trataría de hallar el vector que une los dos puntos y hacer su módulo:
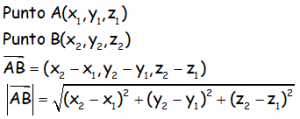
EJEMPLO M2BE3465:
Hallar la distancia del punto A(3,2,1) al punto B (5,3,0).
RESOLUCIÓN:
Obtenemos el vector AB (o el BA) y hallamos el módulo
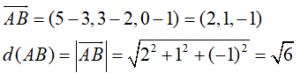
DISTANCIA DE UN PUNTO A UNA RECTA:
Se entiende que la distancia de un punto a una recta es la menor de las infinitas distancias de todos los puntos de la recta al punto dado. De hecho es la longitud del segmento perpendicular a la recta que va desde ella al punto dado.
Es el módulo del vector que une el punto dado P, con el punto P’ (proyección de P sobre la recta-“punto de enfrente”-). Existen tres formas iniciales de calcular esta distancia, que nombraremos:
- Por punto de enfrente.
- Por mínimos.
- Por producto escalar.
POR PUNTO DE ENFRENTE:
Se trata de encontrar el punto P’ de la recta, ya que el módulo del vector (PP’)* es la distancia buscada.
La forma de encontrarlo es pensar que el punto de enfrente está en un plano que pasa por P y es perpendicular a la recta r. De hecho, la intersección de ese plano y la recta nos da P’ ( el punto de enfrente).
La ecuación del plano es sencilla, ya que tenemos un punto, el P y un vector perpendicular al plano, el director de r. Con la ecuación normal del plano, ya lo tenemos. La intersección del plano y de r, nos da P’. El módulo de PP’ es la distancia pedida.
EJEMPLO M2BE3466:
Calcular la distancia del punto P(0,11,0) a la recta determinada por las ecuaciones:
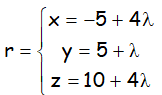
RESOLUCIÓN POR PUNTO DE ENFRENTE:
El plano que pasa por P(0,11,0) y es perpendicular a r, se obtiene con la ecuación normal del plano, con el director de la recta como el vector normal al plano y el punto P como un punto del plano.

POR MINIMOS:
Se trata en este caso, de buscar una expresión general de los vectores que unen P con cualquier punto de la recta y encontrar cuál de todos ellos tiene el módulo mínimo.
EJEMPLO M2BE3467:
Hallar la distancia del P(5 ,6 ,6) a la recta r: (5λ , 2-λ , λ)
SOLUCIÓN POR MÍNIMOS:
La distancia de un punto genérico de la recta (5λ , 2-λ , λ) al punto P es el módulo de este vector que vamos a llamar RP (las componentes de P menos las de R):
![]()
Esta es la expresión general de “todas las distancias” desde P hasta la recta. a nosotros nos interesa la que es mínima.
Podemos utilizar la teoría de máximos y mínimos para esto de forma rigurosa, pero es más breve pensar que la raíz es mínima si lo es el radicando, que es más fácil de trabajar:
Derivada igual a cero y sustituir en segunda:
54λ – 54 = 0; λ = 1 que es un mínimo ya que la 2º derivada es siempre positiva.
Para λ = 1 la distancia es mínima e igual a:
![]()
POR PRODUCTO ESCALAR:
En este otro caso, la idea que se utiliza para calcular el punto de enfrente, el punto P’ de la recta más cercano al punto P dado, es pensar que de todos los vectores posibles que unen P con cualquier punto de la recta (vector RP ) el que nos interesa es perpendicular a la recta (al director de la recta) y por lo tanto, por las propiedades del producto escalar para vectores perpendiculares, el producto d · RP = 0 (de este vector genérico con el director de la recta es cero).
Haremos el mismo ejemplo anterior con este método.
EJEMPLO M2BE3467:
Hallar la distancia del P(5,6,6) a la recta r: (5λ , 2-λ , λ).
SOLUCIÓN POR PRODUCTO ESCALAR:
El vector RP genérico (las componentes de P menos las de R), lo vimos antes es: (5-5λ , 4+λ , 6-λ), el RP particular que buscamos es perpendicular a la recta. Por ello su producto escalar con el director de la recta d = (5,-1,1) será igual a cero.
![]()
O sea que el vector RP que nos interesa es el (0,5,5), (introduciendo en el genérico el valor de λ) que tiene de módulo la distancia pedida y es igual a:
![]()
DISTANCIA DE UN PUNTO A UN PLANO:
Igual que en el caso de la distancia de un punto a una recta, se trata de calcular la mínima distancia. El problema consiste también en localizar el “punto de enfrente”. La fórmula final:
La distancia de un punto P(xo,yo,zo), a un plano p: ax + by+ cz + d = 0 se puede obtener:
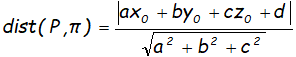
DISTANCIA ENTRE DOS RECTAS:
Si las rectas se cortan, la distancia es cero.
Si son paralelas, tomamos un punto de una de ellas y calculamos la distancia de ese punto a la otra recta. Lo sabemos hacer por el apartado anterior.
Si se cruzan: Se trata de entender en primer lugar, a la vista del dibujo, que la mínima distancia entre ellas es la del segmento que es perpendicular a las dos rectas. Buscamos la expresión del vector genérico que une un punto genérico de una recta, con un punto genérico de la otra recta. Una vez tengamos la expresión de este vector genérico que une r con s, le hacemos cumplir la condición de que sea perpendicular a los directores de cada una de las rectas, teniendo que cumplirse que el producto escalar con los dos directores es cero.
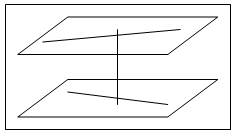
EJEMPLO M2BE3468:
Calcular la distancia entre las rectas: r: (13+12λ , 2 , 8+5λ) y s: (6 , 6+μ , -9).
La forma paramétrica en la que están expresadas las dos rectas es ideal (pensar que es necesario que cada una de ellas esté expresada en función de un parámetro diferente, como es nuestro caso), ya que un punto genérico de r es precisamente R (13+12l , 2, 8+5l) y el punto genérico de s es S (6, 6+μ , -9), por ello el vector RS será las componentes de S menos las de R, con lo que:
RS = (-7-12λ , 4+μ , -17-5λ).
Este vector RS tiene que ser perpendicular a la recta r y a la recta s, por lo que su producto escalar con cada uno de los directores d (12, 0, 5) de r y d’ (0, 1, 0) de s tiene que ser cero:
RS · d = 0 ; (-7-12λ , 4+μ , -17-5λ) · (12, 0, 5) = 0
RS · d’ = 0 ; (-7-12λ , 4+μ , -17-5λ) · (0,1,0) = 0
De aquí sale un sistema de dos ecuaciones con dos incógnitas que son λ y μ.
λ sustituida en la ecuación de r nos da el punto de r inicio del segmento buscado y μ sustituido en s nos da el punto fin del segmento que buscamos.
La distancia pedida será el módulo del vector que va de este punto inicio al punto fin. La solución del ejercicio es 13.
DISTANCIA DE UNA RECTA A UN PLANO:
Sólo tiene sentido si la recta y el plano son paralelos, en cuyo caso se calcula la distancia de un punto de la recta (se obtiene fácilmente de la ecuación en cualquiera de sus formas) al plano.
Lo primero que hay que mirar es si realmente son paralelos, fijándose en los vectores director de la recta y normal al plano, que tienen que ser perpendiculares. Si no son paralelos directamente, la distancia es cero.
DISTANCIA ENTRE DOS PLANOS:
Igual que antes sólo tiene sentido si los dos planos son paralelos, en cualquier otro caso, la distancia sería cero.
Si los dos planos son paralelos, se calcula la distancia de un punto de cualquiera de ellos al otro plano. Lo único necesario aclarar es que un punto de cualquiera de los dos planos lo podemos obtener dando valores a x y a y y obteniendo por ejemplo la z; éste sería uno de los infinitos puntos del plano.
Lo primero que hay que comprobar es que los planos son paralelos fijándose en las componentes del vector normal. Si no son paralelos se responde directamente que la distancia es cero.
