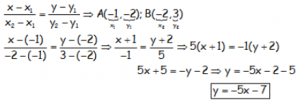EJERCICIO RESUELTO FUNCIONES RECTAS
EJERCICIO RESUELTO DE FUNCIONES LINEALES. RECTAS: CARACTERÍSTICAS Y REPRESENTACIÓN:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
FORMA PARTE DE LOS MATERIALES DE LAS PROGRAMACIONES DIDÁCTICAS:
EJERCICIO M4EP310:
Calcular las ecuaciones de las rectas siguientes, sabiendo que:
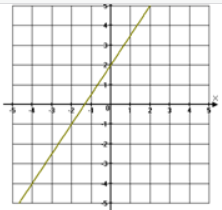
a) Esta es su representación gráfica:
b) Tiene una ordenada en el origen -2 y pendiente 1.
c) m= -1 y n= 3
d) La pendiente es 3 y pasa por el punto A(-2,0)
e) La ordenada en el origen es 1 y pasa por el punto A(-2,2)
f) Pasa por los puntos: A(1,2) y B(-1,3)
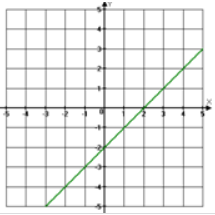
g) Esta es su gráfica:
h) Ordenada en el origen 1 y pendiente 3.
i) m= 1/2 y n= -4
j) La pendiente es 1 y pasa por el punto A(2,3)
k) La ordenada en el origen es 2 y pasa por el punto A(-1,2)
l) Pasa por los puntos: A(-1,-2) y B(-2,3).
RESOLUCIÓN DEL EJERCICIO:
Calcular las ecuaciones de las rectas siguientes, sabiendo que:
a) Esta es su representación gráfica:
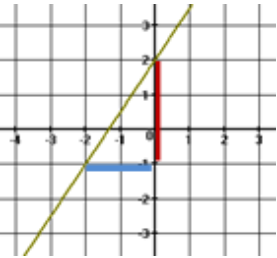
Notar como de la representación gráfica, la ordenada en el origen es 2 y la pendiente que es igual a la distancia vertical/distancia horizontal es igual a 3/2.
Por ello, la ecuación de la recta es y = mx + n
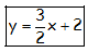
b) Tiene una ordenada en el origen -2 y pendiente 1.
Clarísimo: y = mx + n, por lo tanto y = x – 2
c) m= -1 y n= 3
Lo mismo: y = – x + 3
d) La pendiente es 3 y pasa por el punto A (-2,0):
Como la pendiente es 3, su ecuación en principio será: y = 3x + n , donde lo único que nos falta es n (ordenada en el origen)
Como pasa por el punto A(-2,0), la ecuación de la recta tiene que cumplirse para ese punto, puesto que pertenece a la recta. Por ello:
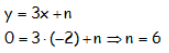
La ecuación de la recta es por lo tanto: y = 3x + 6
e) La ordenada en el origen es 1 y pasa por el punto A (-2,2):
Como la ordenada es n=1, la ecuación de la recta es y = mx + 1, donde nos falta obtener el valor de la pendiente m.
Por pasar por el punto A(2,2):
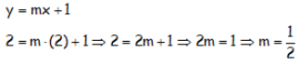
La recta entonces es: y = 1/2 x + 1
f) Pasa por los puntos: A (1,2) y B (-1,3)
De la ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS A(x1,y1) y B(x2,y2):
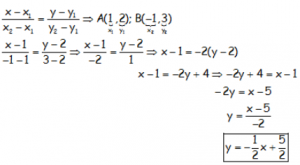
g) Esta es su gráfica:

De la gráfica obtenemos la pendiente = m = 1; la ordenada = n = -2. Por lo tanto:
La ecuación es: y = x – 2
h) Ordenada en el origen 1 y pendiente 3.
Su ecuación es y = 3x – 1
i) m = 1/2 y n = – 4
y = 1/2 x – 4
j) La pendiente es 1 y pasa por el punto A (2,3):
Como la pendiente es 1, su ecuación en principio será: y = x + n , donde lo único que nos falta es n (ordenada en el origen)
Como pasa por el punto A(2,3), la ecuación de la recta tiene que cumplirse para ese punto, puesto que pertenece a la recta. Por ello:
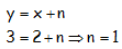
La ecuación de la recta es por lo tanto: y = x + 1
k) La ordenada en el origen es 2 y pasa por el punto A (-1,2):
Como la ordenada es n=2, la ecuación de la recta es y=mx+2, donde nos falta obtener el valor de la pendiente m.
Por pasar por el punto A (-1,2):
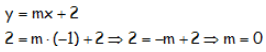
La recta es entonces y = 2.
l) Pasa por los puntos: A (-1,-2) y B (-2,3):
De la ECUACIÓN DE LA RECTA QUE PASA POR DOS PUNTOS A (x1,y1) y B (x2,y2):