EJERCICIOS RESUELTOS INTEGRALES PARTES
RESOLUCIÓN DE LOS EJERCICIOS M2BE1890 DE INTEGRALES POR PARTES:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
- CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
- MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE. EJEMPLOS RESUELTOS
- EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
SIGUE EL PROCESO DETERMINADO POR:
EJERCICIOS M2BE1890:
Resolver las siguientes integrales:
RESOLUCIÓN DE LOS EJERCICIOS:
En el primer ejemplo hay que aplicar el método «POR PARTES» dos veces, ya que se baja el grado de la expresión polinómica una unidad cada vez.
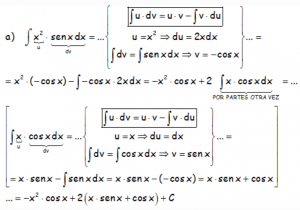
Notar que hemos tenido que aplicar el método dos veces, porque con cada vez se baja un grado la función polinómica.
Lo más complicado es saber qué tenemos que llamar “u” y que “dv”. Habremos elegido bien si la integral que nos queda después de aplicar el método es más sencilla que la original, habría que cambiar el criterio en caso contrario.
La palabra “ALPES”, ayuda a realizar la elección correcta. “A” son funciones arco, “L” logarítmicas, “P” polinómicas, “E” exponenciales, “S” senos y cosenos. Hay que elegir según esto «u» aquella función cuya letra aparezca primero en “ALPES”.
Igualmente estos otros ejemplos:
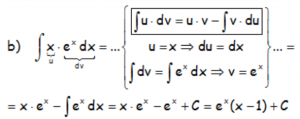
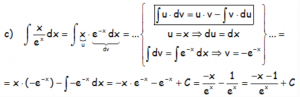
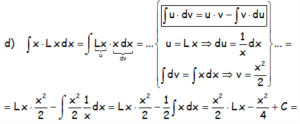
En los casos siguientes, se resuelven por partes, pero “u” está claro, ya que hay una única expresión y “dv=dx”.
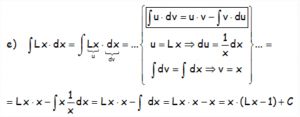
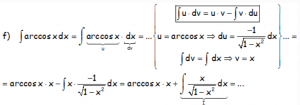
Notar que esta última integral, que hemos llamado «I» que nos queda puede resolverse por sustitución:
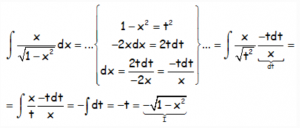
Con lo que la integral, añadiendo este último resultado:
![]()