GEOMETRÍA ESPACIAL ECUACIONES PLANO
GEOMETRÍA ESPACIAL. ECUACIONES DEL PLANO EN TRES DIMENSIONES:

PODRÍA INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
-
- GEOMETRÍA PLANA PARA SECUNDARIA Y 1º DE BACHILLERATO
- GEOMETRÍA ESPACIAL PARA BACHILLERATO
- GEOMETRÍA ESPACIAL. ECUACIONES DE LA RECTA EN 3 DIMENSIONES
- POSICIONES RELATIVAS DE DOS RECTAS EN EL ESPACIO, PARA MATEMÁTICAS II DE 2º BACHILLERATO
- CONDICIÓN DE PUNTOS ALINEADOS. GEOMETRÍA ESPACIAL PARA BACHILLERATO. EJERCICIOS RESUELTOS
- CONDICIÓN DE PUNTOS COPLANARIOS. GEOMETRÍA ESPACIAL PARA BACHILLERATO. EJERCICIOS RESUELTOS
FORMA PARTE DE LOS MATERIALES DE LA PROGRAMACIÓN DIDÁCTICA:
ECUACIONES DEL PLANO. GEOMETRÍA EN 3D PARA SEGUNDO DE BACHILLERATO:
Para determinar un PLANO de forma inequívoca necesitamos un punto QUE PERTENEZCA AL PLANO y dos vectores, contenidos en el plano (paralelos al plano) pero NO PARALELOS ENTRE SÍ, o bien un único vector perpendicular al plano (ecuación normal del plano).
Las diferentes formas de expresar un PLANO:
ECUACIÓN DEL PLANO EN FORMA VECTORIAL:
![]()
Donde:
![]()
es un punto del plano
![]()
son dos vectores del plano, no paralelos entre sí
ECUACIONES DEL PLANO EN FORMA PARAMÉTRICA:
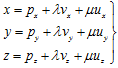
Que se obtienen de la ECUACIÓN VECTORIAL DEL PLANO igualando componente a componente.
ECUACIÓN DEL PLANO EN FORMA IMPLÍCITA:
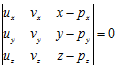
Que parte de la idea de que la matriz correspondiente al determinante que se muestra tiene que tener rango dos, con lo que su determinante de orden tres tiene que ser igual a cero.
ECUACIÓN GENERAL DEL PLANO:
Haciendo operaciones en el determinante anterior, ordenando, e igualando a cero nos queda:
ax + by +cz + d = 0
que es la ecuación general del plano. Donde a, b y c son los coeficientes que resultan al hacer operaciones de cada una de las componentes x, y, z.
Veremos como el vector formado por (a, b, c) corresponde a un vector normal (perpendicular al plano).
ECUACIÓN NORMAL DEL PLANO:
Por las propiedades del producto escalar, cuando multiplicamos escalarmente un vector perpendicular al plano y un vector contenido en el plano nos tiene que dar cero. De esta idea obtenemos:
![]()
Que es la ecuación normal del plano, donde:
![]()
es un punto del plano. y
v = (a,b,c) es un vector perpendicular al plano.
Debemos notar que esta ecuación del plano es muy interesante, ya que con un vector perpendicular, sólo uno, y un punto, determinamos un plano. En todas las otras formas de expresar un plano, necesitamos dos vectores, al ser paralelos al plano. En física tienen esto muy claro: las superficies en física, se representan mediante vectores perpendiculares a las superficies.
RESUMEN DE FÓRMULAS DE GEOMETRÍA ESPACIAL PARA 2º DE BACHILLERATO:
