PARÁBOLAS FUNCIONES CUADRÁTICAS REPRESENTACIÓN
PARÁBOLAS: FUNCIONES CUADRÁTICAS, POLINÓMICAS DE SEGUNDO GRADO. REPRESENTACIÓN Y CARACTERÍSTICAS:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
FORMA PARTE DE LOS MATERIALES DE LAS PROGRAMACIONES DIDÁCTICAS:
REPRESENTACIÓN DE FUNCIONES CUADRÁTICAS (PARÁBOLAS):
Las funciones polinómicas de segundo grado del tipo:
f(x) = a x2 + b x + c
al representarlas nos queda una parábola: curva sencilla abierta hacia arriba o hacia abajo dependiendo del signo de a (coeficiente que acompaña a la x2).
- Tienen un vértice que puede ser máximo o mínimo.
Si a es positivo (a > 0) la parábola está abierta hacia arriba y el vértice es un mínimo.
Si a es negativo (a < 0) la parábola está abierta hacia abajo y el vértice es negativo.
- Las parábolas son curvas simétricas respecto a rectas verticales que pasan por su vértice.
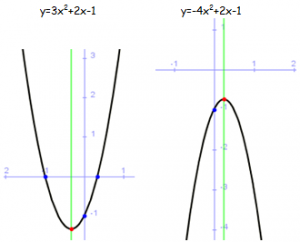
Ejemplos de Parábolas:
Cuando nos piden que representemos una parábola, lo primero sería encontrar el VÉRTICE de la parábola, que se encuentra en el punto en el que la x vale -b / 2a ; la y del vértice la podemos obtener sustituyendo la x en la ecuación de la parábola.
Después los PUNTOS DE CORTE con cada uno de los ejes:
Con el eje horizontal (eje x) cuando la y = 0; esto nos obligará en el caso de las parábolas a resolver la ecuación de segundo grado.
Con el eje vertical (eje y) cuando la x = 0, nos dará el término independiente (la c de la función).
Si con estos puntos obtenidos: vértice y cortes con los ejes no podemos representar con más o menos exactitud la parábola, debemos dar valores a la x a puntos a ambos lados del vértice donde sea conveniente para ver mejor la “silueta” de la parábola.
EJEMPLO:
Representar la función y = x2 + 2x + 1
RESOLUCIÓN:
Lo primero caer en la cuenta que está abierta hacia arriba, ya que el coeficiente que acompaña a la x2 es positivo, de hecho a=1.
Para el cálculo del Vértice:
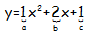
El vértice estará en:
![]()
Por ello, la y del vértice, sustituyendo la x en la expresión de la función:
![]()
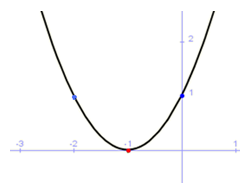
Con lo que el vértice será el punto V (-1,0)
PUNTOS DE CORTE CON LOS EJES:
Corte con el eje OX, cuando la y vale cero:
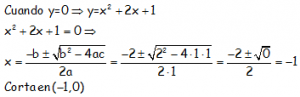
Notar como el corte con el eje X coincide con el vértice.
Para los cortes con el eje OY, cuando la x vale cero:
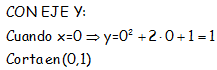
REPRESENTACIÓN:
Teniendo en cuenta que sólo tenemos dos puntos (el vértice y un punto a la derecha de él) estaría bien obtener otro punto a la izquierda del vértice, por ejemplo en x=-1; haciendo la tabla de valores:
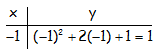
Con lo que la parábola sería:
EJEMPLO M4EE1904:
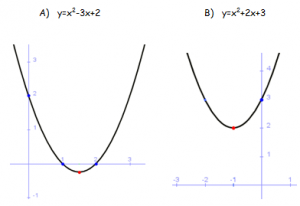
Comprobar que las siguientes funciones cuadráticas, haciendo los cálculos necesarios, se corresponden con la representación que se aporta:
a) y = x2 – 3x + 2
b) y = x2 + 2x + 3
SOLUCIÓN: