PUNTOS ALINEADOS GEOMETRÍA ESPACIAL
CONDICIÓN DE PUNTOS ALINEADOS. GEOMETRÍA ESPACIAL PARA BACHILLERATO. EJERCICIOS RESUELTOS:

PODRÍA INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
-
- GEOMETRÍA PLANA PARA SECUNDARIA Y 1º DE BACHILLERATO
- GEOMETRÍA ESPACIAL PARA BACHILLERATO
- GEOMETRÍA ESPACIAL. ECUACIONES DE LA RECTA EN 3 DIMENSIONES
- POSICIONES RELATIVAS DE DOS RECTAS EN EL ESPACIO, PARA MATEMÁTICAS II DE 2º BACHILLERATO
- GEOMETRÍA ESPACIAL. ECUACIONES DEL PLANO EN TRES DIMENSIONES
- CONDICIÓN DE PUNTOS COPLANARIOS. GEOMETRÍA ESPACIAL PARA BACHILLERATO. EJERCICIOS RESUELTOS
FORMA PARTE DE LOS MATERIALES DE LA PROGRAMACIÓN DIDÁCTICA:
CONDICIÓN DE PUNTOS ALINEADOS, PARA GEOMETRÍA DE BACHILLERATO:
Dos puntos siempre están alineados ya que dos puntos determinan una recta.
Sin embargo, tres o más puntos:
![]()
están alineados si de los vectores
![]()
sólo hay uno linealmente independientes, es decir el rango de la matriz formada por ellos es 1.
En este caso, ese vector independiente será el director de la recta en la que se encuentran los tres puntos.
EJERCICIOS RESUELTOS CON ESTA ESTRATEGIA DEL RANGO DE LOS VECTORES:
EJERCICIO M2BE1838:
Estudiar si los puntos A(2,0,3); B(3,2,1); C(2,1,0) están alineados.
RESOLUCIÓN:
Con los puntos obtenemos los vectores:

Que como se ve, sin necesidad de estudiar rangos, se ve que los dos son linealmente independientes, no están alineados.
EJERCICIO M2BE1695:
Hallar a y b para que A(1,1,-1), B(2,-3,4) y C(0, a, b+1) estén alineados.
RESOLUCIÓN:
Tenemos que obtener los vectores:
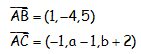
Para que estén alineados, los dos vectores tienen que ser dependientes, entonces:
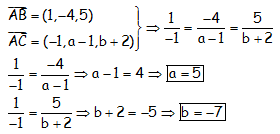
UTILIZANDO LA ESTRATEGIA DE CONSTRUIR UNA RECTA CON DOS DE LOS PUNTOS:
No obstante lo anterior, la estrategia más intuitiva es, cuando te dan tres puntos ( con más sería un proceso muy largo), obtener alguna ecuación de la recta que pasa por dos de ellos y ver si el tercero cumple la ecuación, en cuyo caso estarían alineados.
EJERCICIO M2BE2244: EBAU CANARIAS JUNIO 2014
Dados los puntos A (-1,0,3), B (2,4,1) y C (-4,3,1):
a.- Estudiar si los puntos A,B y C están alineados.
b.- Hallar la ecuación de la recta paralela al segmento AB y que pasa por C. Expresarla como intersección de dos planos.
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA
EJERCICIO M2BE2159:
Sean los puntos A (3, 1, 5), B (-2, -1, 4) y C (8, 3, 6).
a) Demostrar si los tres puntos están alineados o no.
b) Calcular la recta s perpendicular a la recta determinada por A y B, sabiendo que s pasa por P(-2, 3, -1).
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN GEOMETRÍA, ÁLGEBRA, ANÁLISIS PARA MATEMÁTICAS 2º BACHILLERATO
EJERCICIO M2BE2359:
a.- ¿Están alineados los puntos A(3,-2,1), B(5,-6,9) y C(4,4,5)?.
b.- Calcular el plano perpendicular a la recta AB que pasa por C.
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/HaZzkoXgjmg
RESUMEN DE FÓRMULAS DE GEOMETRÍA ESPACIAL PARA 2º DE BACHILLERATO:
