PUNTOS COPLANARIOS EJERCICIOS RESUELTOS
CONDICIÓN DE PUNTOS COPLANARIOS. GEOMETRÍA ESPACIAL PARA BACHILLERATO. EJERCICIOS RESUELTOS:

PODRÍA INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
-
- GEOMETRÍA PLANA PARA SECUNDARIA Y 1º DE BACHILLERATO
- GEOMETRÍA ESPACIAL PARA BACHILLERATO
- GEOMETRÍA ESPACIAL. ECUACIONES DE LA RECTA EN 3 DIMENSIONES
- POSICIONES RELATIVAS DE DOS RECTAS EN EL ESPACIO, PARA MATEMÁTICAS II DE 2º BACHILLERATO
- GEOMETRÍA ESPACIAL. ECUACIONES DEL PLANO EN TRES DIMENSIONES
- CONDICIÓN DE PUNTOS ALINEADOS. GEOMETRÍA ESPACIAL PARA BACHILLERATO. EJERCICIOS RESUELTOS
FORMA PARTE DE LOS MATERIALES DE LA PROGRAMACIÓN DIDÁCTICA:
CONDICIÓN DE PUNTOS COPLANARIOS:
Tres puntos siempre son coplanarios, ya que tres puntos determinan un plano.
Cuatro o más puntos:
![]()
serán coplanarios si de los vectores
![]()
sólo hay dos linealmente independientes, es decir el rango de la matriz formada por ellos es 2.
Esos dos vectores independientes son los dos vectores que determinan la dirección del plano y que se usan en las ecuaciones del plano.
EJERCICIOS RESUELTOS UTILIZANDO ESTA ESTRATEGIA DE LOS RANGOS:
EJERCICIO M2BE1839:
Estudiar si los puntos A(2,0,3); B(3,2,1); C(2,1,0); D(3,2,1) son coplanarios.
RESOLUCIÓN:
Con los puntos obtenemos los vectores:
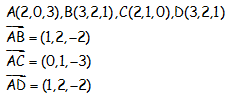
Que como se ve, sin necesidad de estudiar rangos, se ve que hay dos linealmente independientes, son coplanarios.
EJERCICIO M2BE1694:
Hallar a para que los puntos A(1,-1,2); B(-2,1,3), C(0,1,0) y D(a-1, a+1, 2) sean coplanarios.
RESOLUCIÓN:
Tenemos que obtener los vectores:
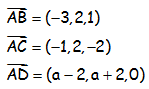
Para que sean coplanarios, de los tres vectores sólo pueden haber 2 linealmente independientes, es decir, el rango de la matriz formada por ellos tiene que ser 2; o lo que es lo mismo, el determinante de esa matriz tiene que ser igual a cero (y confirmar que quedan dos independientes, no uno sólo):
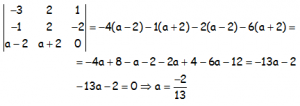
Observar que los dos primeros vectores son independientes, ya que no son proporcionales, que se ve bien a ojo (cuando tenemos dos vectores, la única posibilidad de ser dependientes es que sean proporcionales; si tenemos tres o más uno de ellos podría ser combinación lineal de los otros y no ser sencillo de ver a ojo).
EJERCICIOS RESUELTOS UTILIZANDO LA ESTRATEGIA DE CONSTRUIR UN PLANO CON TRES DE LOS PUNTOS:
Con frecuencia se trabaja de este otro modo: construimos un plano, en cualquiera de sus ecuaciones, con tres de los puntos que nos dan y comprobamos que el cuarto punto, o los otros dados, cumplen la ecuación del plano anterior. En ese caso serían coplanarios.
EJERCICIO M2BE1989JL (EBAU CANARIAS 2021):
Dados los siguientes puntos en el espacio tridimensional: A(0,-2,3), B(1,-1,4), C(2,3,3) y D(4,5,5)
a.- Comprobar que los cuatro puntos son coplanarios. A continuación, calcular la ecuación del plano que los contiene.
b.- Calcular la ecuación de la recta r, perpendicular al plano π, que pasa por el punto A.
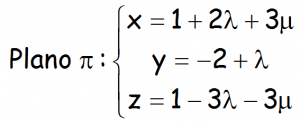
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/SYfqOEhBSw4
EJERCICIO M2BE2385, EBAU CANARIAS 2021:
Dados los siguientes puntos en el espacio tridimensional:
A(0, -2, 3), B(1, -1, 4), C(2, 3, 3) y D(4, 5, 5)
a.- Comprobar que los cuatro puntos son coplanarios. A continuación, calcular la ecuación del plano que los contiene.
b.- Calcular la ecuación de la recta r, perpendicular al plano π, que pasa por el punto A, siendo π el plano siguiente :
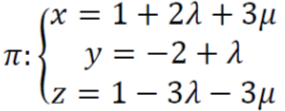
RESUMEN DE FÓRMULAS DE GEOMETRÍA ESPACIAL PARA 2º DE BACHILLERATO:
