EJERCICIOS RESUELTOS DE INTEGRALES TRIGONOMÉTRICAS

EJERCICIOS RESUELTOS INTEGRALES TRIGONOMÉTRICAS

EJERCICIOS RESUELTOS DE INTEGRALES TRIGONOMÉTRICAS:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

• • TABLA DE DERIVADAS
  • TABLA DE INTEGRALES INMEDIATAS
• MÉTODOS DE INTEGRACIÓN PARA INTEGRALES TRIGONOMÉTRICAS
• DEMOSTRACIÓN DE LAS EXPRESIONES DE LA «SUSTITUCIÓN UNIVERSAL» EN INTEGRALES TRIGONOMÉTRICAS
• CÁLCULO DE INTEGRALES PARA MATEMÁTICAS DE BACHILLERATO
• MÉTODO DE INTEGRACIÓN POR SUSTITUCIÓN O CAMBIO DE VARIABLE. EJEMPLOS RESUELTOS
• EJERCICIOS RESUELTOS DE INTEGRALES POR SUSTITUCIÓN O CAMBIO DE VARIABLE PARA MATEMÁTICAS DE 2º DE BACHILLERATO
• MÉTODO DE INTEGRACIÓN POR PARTES DE RESOLUCIÓN DE INTEGRALES PARA BACHILLERATO
• INTEGRACIÓN DE FUNCIONES RACIONALES
• MÉTODO DE INTEGRACIÓN PARA INTEGRALES IRRACIONALES. CÁLCULO INTEGRAL

SIGUE EL PROCESO DETERMINADO POR:

• MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA

EJERCICIO M2BE3245:

RESOLUCIÓN DE LA INTEGRAL:

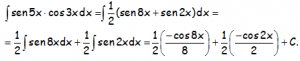
EJERCICIO M2BE3246:

RESOLUCIÓN DE LA INTEGRAL:

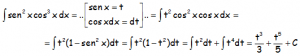
EJERCICIO M2BE3247:

RESOLUCIÓN DE LA INTEGRAL:

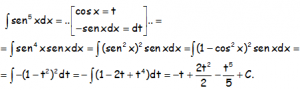
EJERCICIO M2BE3248:

RESOLUCIÓN DE LA INTEGRAL:

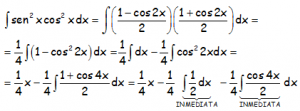
EJERCICIO M2BE3249:

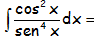
RESOLUCIÓN DE LA INTEGRAL:

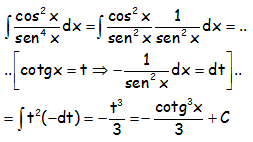
EJERCICIO M2BE3250:

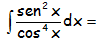
RESOLUCIÓN DE LA INTEGRAL:

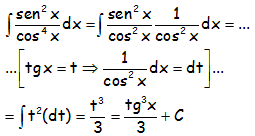
EJERCICIO M2BE3251:

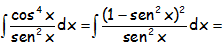
RESOLUCIÓN DE LA INTEGRAL:

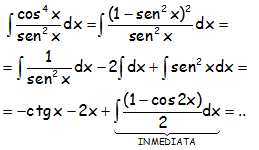
EJERCICIOS M2BE3252:

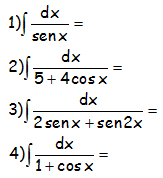
INDICACIONES PARA LA RESOLUCIÓN DE ESTAS INTEGRALES:

• • Sustituyendo las expresiones de sen x, cos x, dx de la sustitución universal se transforman en racionales sencillas.

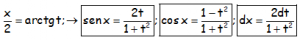
• • Tener en cuenta en el ejemplo 3) hay que inicialmente utilizar la transformación: sen 2x=2 senx cosx
  • El ejemplo 4) también se resuelve fácilmente multiplicando numerador y denominador por el conjugado del denominador.