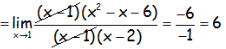INDETERMINACIÓN COCIENTE DE CEROS
INDETERMINACIÓN CERO DIVIDIDO ENTRE CERO. COCIENTE DE CEROS (0/0):

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- LÍMITES PARA MATEMÁTICAS DE BACHILLERATO
- REGLA DE L’HÔPITAL PARA EL CÁLCULO DE LÍMITES. MATEMÁTICAS BACHILLERATO
- INFINITÉSIMOS EQUIVALENTES PARA EL CÁLCULO DE LÍMITES (ampliación de contenidos)
- FUNCIONES: ANÁLISIS PARA 1º BACHILLERATO
- EJERCICIOS DE ANÁLISIS DE FUNCIONES
ESTÁ EN CONSONANCIA CON LAS ESTRATEGIAS DETERMINADAS POR LAS PROPUESTAS DE PROGRAMACIONES:
- MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS II DE 2º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
- MATEMÁTICAS II APLICADAS A LAS CIENCIAS SOCIALES PARA 2º DE BACHILLERATO. DESARROLLO DE LA ASIGNATURA
INDETERMINACIÓN (0/0):
Este tipo de indeterminación, se suele presentar en cocientes de polinomios; cuando calculamos límites en un punto en el que se nos anula tanto el numerador como el denominador. Para resolver la indeterminación hay que descomponer en factores los polinomios, tanto del Numerador como del Denominador (utilizando Ruffini, ecuación de segundo grado, productos notables….) y se genera el factor nulo en numerador y denominador, que al simplificarlo conduce a la resolución de la indeterminación.
En ocasiones, si esta indeterminación aparece asociada a raíces, binomios de raíces, se hace necesario multiplicar y dividir por el conjugado del binomio de raíces, para que «asome» el factor nulo.
Ya con más nivel, se pueden utilizar:
- REGLA DE L’HÔPITAL PARA EL CÁLCULO DE LÍMITES. MATEMÁTICAS BACHILLERATO
- INFINITÉSIMOS EQUIVALENTES PARA EL CÁLCULO DE LÍMITES (ampliación de contenidos)
EJERCICIO M1BE1836:
Hallar el siguiente límite:
RESOLUCIÓN DEL EJERCICIO:
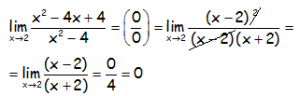
EJERCICIO M1BE119b:
Hallar el siguiente límite:
RESOLUCIÓN DEL EJERCICIO:
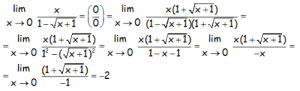
EJERCICIO M1BE1837:
Hallar el siguiente límite:
RESOLUCIÓN DEL EJERCICIO:

Por Ruffini, buscando descomponer en factores tanto el numerador como el denominador:
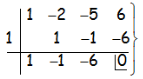
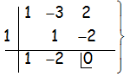
Nos queda: