PROBLEMA OPTIMIZACIÓN RESUELTO ROMBO
EJERCICIO RESUELTO M2BE2239, PROBLEMA DE OPTIMIZACIÓN EBAU CANARIAS JUNIO 2013:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
-
- TABLA DE DERIVADAS
- CURSO DE CÁLCULO DE DERIVADAS PARA BACHILLERATO
- CÁLCULO DE DERIVADAS PARA MATEMÁTICAS DE BACHILLERATO
- RECETA PARA ESTUDIAR CRECIMIENTO Y CURVATURA (CONCAVIDAD Y CONVEXIDAD) DE UNA FUNCIÓN, MÁXIMOS, MÍNIMOS Y PUNTOS DE INFLEXIÓN
- APLICACIONES DE LA DERIVADA: MONOTONÍA Y CURVATURA PARA MATEMÁTICAS DE BACHILLERATO. EJERCICIOS RESUELTOS
- TABLA DE DERIVADAS
INDICACIONES PARA RESOLVER PROBLEMAS DE OPTIMIZACIÓN:
-
- LEER TANTAS VECES EL EJERCICIO QUE CASI LO SEPAS DE MEMORIA!!!, ya que son en ocasiones difíciles de interpretar. Cuando el ejercicio de optimización consista en una situación relacionada con la geometría, dibujar la situación, poniendo nombre a cada uno de los elementos que intervienen en el ejercicio.
- Identificar la función objeto de máximo o mínimo (qué queremos que sea máximo o mínimo: superficie, volumen, distancia, tiempo….)
- Ponerla en función de una sola variable, utilizando los datos del problema. (ojo que a veces es mejor una variable que la otra a la hora de derivar)
- Una vez la función objeto de máximo o mínimo está en función de una sola variable, derivarla e igualarla a cero. Al resolver esta ecuación tenemos los posibles Máximos o mínimos.
- Confirmar el máximo o mínimo:
- LEER TANTAS VECES EL EJERCICIO QUE CASI LO SEPAS DE MEMORIA!!!, ya que son en ocasiones difíciles de interpretar. Cuando el ejercicio de optimización consista en una situación relacionada con la geometría, dibujar la situación, poniendo nombre a cada uno de los elementos que intervienen en el ejercicio.
Si la segunda derivada es fácil de calcular, sustituir los posibles máximos o mínimos en la segunda derivada (Recordar que si al sustituir es negativa tenemos un Máximo y si positiva mínimo)
Si es complicado el cálculo de la segunda, utilizar la primera derivada, sustituyendo un punto por encima y otro por debajo del posible máximo o mínimo y recordar que antes de un máximo la función es creciente (1ª derivada positiva) y después decreciente (1ª derivada negativa). En un mínimo antes es exactamente lo contrario: decreciente primero y después creciente.
EJERCICIO M2BE2239: EBAU CANARIAS JUNIO 2013
La figura siguiente muestra un rombo inscrito dentro de un rectángulo, de forma que los vértices del rombo se sitúan en los puntos medios de los lados del rectángulo. El perímetro del rectángulo es de 100 metros. Calcular las longitudes de sus lados para que el área del rombo inscrito sea máxima.
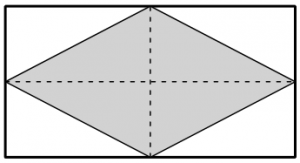
RESOLUCIÓN DEL EJERCICIO: