SOLUCIONES SISTEMAS ECUACIONES 3X3
SISTEMAS LINEALES REGLA CRAMER
SOLUCIONES DE LOS EJERCICIOS DE SISTEMAS DE ECUACIONES LINEALES (3X3) CONTEXTUALIZADOS PARA MATEMÁTICAS DE BACHILLERATO. REGLA DE CRAMER:

INTERESA LA CONSULTA DEL SIGUIENTE ARTÍCULO, CON TEORÍA Y EJERCICIOS RESUELTOS Y PROPUESTOS:
FORMA PARTE DEL PROCESO DETERMINADO POR LAS PROGRAMACIONES DIDÁCTICAS DE MATEMÁTICAS DE BACHILLERATO:
EJERCICIO M1BE2077:
Durante una hora, una agencia de viajes vende un total de 30 billetes de avión con destino a las islas de La Palma, Gran Canaria y Lanzarote. Sabiendo que los billetes para Gran Canaria representan el doble de los emitidos para las otras dos islas, y que los correspondientes a Lanzarote son la mitad de los emitidos para La Palma más cuatro:
a) Plantear el correspondiente sistema de ecuaciones.
b) Determinar el número de billetes para cada una de las tres islas.
SOLUCIÓN:
-
- x = «destino La Palma»
- y = «destino Gran Canaria»
- z = » destino Lanzarote»
-
-
- x + y + z = 30
- y = 2 ( x + z )
- z = 1/2 x +4
-
Solución: x = 4; y = 20; z = 6
EJERCICIO M1BE2078:
En un crucero hay paquetes de tres tipos: individual (1 pasajero), pareja (2 pasajeros) y grupo familiar (4 pasajeros). La tarifa individual es de 800 €, la tarifa de pareja es de 1200 € y la tarifa familiar es de 1600 €. Para el próximo viaje hay 2400 pasajeros que han pagado un total de 1264000 €. Si los pasajeros de individual son el 20% de la suma de los de pareja y de grupo familiar*,
a) Plantear el sistema de ecuaciones para determinar cuántos paquetes de cada tipo integran el crucero.
*NOTA: Prestar especial atención, hay detalles que tenemos que tener en cuenta.
b) Determinar la distribución de los pasajeros en los tres tipos de tarifa.
SOLUCIÓN:
-
- x = «número de paquetes individuales (1 pasajero)»
- y = «número de paquetes de pareja (2 pasajeros)»
- z = » número de paquetes familiares (4 pasajeros)»
-
-
- x + 2y + 4z = 2400 (tener en cuenta el nº de personas por paquete)
- 800 · x + 1200 · y + 1600 · z = 1264000
- x = 20/100 · ( 2y + 4z )
-
Solución: x = 400; y = 360; z = 320; 400 personas en individual, 720 en parejas, 1280 en familia.
EJERCICIO M1BE2083 (EBAU CANARIAS 2021):
Un granjero compra un determinado mes 274 € de pienso para su ganado. Con ese dinero obtiene un total de 66 sacos de pienso de tres marcas diferentes: A, B y C. Se sabe que el precio de cada marca de pienso que ha comprado es de 5 €, 4 € y 4 €, respectivamente. También se sabe que el número de sacos adquiridos de la marca C es el doble que el total de sacos comprados de las marcas A y B juntos. Averiguar la cantidad de sacos que el granjero ha comprado de cada una de las tres marcas.
SOLUCIÓN:
-
- x = «cantidad de sacos de la marca A»
- y = «cantidad de sacos de la marca B»
- z = » cantidad de sacos de la marca C»
-
-
- x + y + z = 66
- 5x + 4y + 4z = 274
- z = 2 · ( x + y )
-
Solución: x = 10; y = 12; z = 44
EJERCICIO M1BE2084 (EBAU CANARIAS 2020):
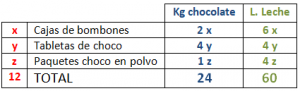
Una pequeña bombonería tiene en su almacén 24 kg de chocolate y 60 litros de leche, con los que elabora tres productos distintos: cajas de bombones, tabletas de chocolate y paquetes de chocolate en polvo. Del resto de los ingredientes se tienen reservas suficientes. Se sabe que las cajas de bombones requieren 2kg de chocolate y 6 litros de leche, las tabletas de chocolate requieren4 kg de chocolate y 4 litros de leche, y cada paquete de chocolate en polvo requiere 1 kg de chocolate y 4 litros de leche. Se quiere fabricar un total de 12 unidades y con ello se consume todo el chocolate y toda la leche almacenados. ¿Cuántas unidades deben fabricarse de cada tipo de producto?
SOLUCIÓN:
-
- x = «cajas de bombones»
- y = «tabletas de chocolate»
- z = «paquetes de chocolate en polvo»

-
-
- x + y + z = 12
- 2x + 4y + z = 24
- 6x + 4y + 4z = 60
-
Solución: x = 6; y = 2; z = 4
EJERCICIO M2BE2260:
La suma de las edades de Carmela, Esperanza y Aurora es 68 años. La edad de Carmela es 5 años más que la mitad de la suma de las edades de Esperanza y Aurora. Además, dentro de 4 años la edad de Aurora será la edad que actualmente tiene Esperanza. Calcular las edades de cada una de ellas.
SOLUCIÓN:
-
- x = «edad de Carmela»
- y = «edad de Esperanza»
- z = » edad de Aurora»
-
-
- x + y + z = 68
- x – 5 = 1/2 ( y + z )
- z + 4 = y
-
Solución: x = 26; y = 23; z = 19
EJERCICIO M1BE2285:
En un grupo de 225 personas, el número de personas sin estudios es igual a la quinta parte de los que tienen estudios primarios. Si por cada 5 personas con estudios primarios hay 3 con estudios secundarios:
a) ¿Cuál es el sistema de ecuaciones que permite calcular el número de personas del grupo por nivel de estudios?.
b) ¿Cuántas personas hay de cada nivel?.
SOLUCIÓN:
-
- x = «sin estudios»
- y = «con estudios primarios»
- z = «con estudios secundarios»
-
-
- x + y + z = 225
- x = 1/5 y
- 3 y = 5 z
-
Solución: x = 25; y =125; z = 75
EJERCICIO M1BE2291:
Se tienen que empaquetar 1500 unidades de un artículo en cajas de 5, 10 y 25 unidades, de manera que haya el triple de cajas de 5 unidades que de 10 unidades y que el número total de cajas sea igual a 90. ¿Cuántas cajas tiene que haber de cada tipo?
SOLUCIÓN:
-
- x = «cajas de 5 unidades»
- y = «cajas de 10 unidades»
- z = » cajas de 25 unidades»
-
-
- 5x + 10y + 25z = 1500
- x = 3 y
- x + y + z = 90
-
Solución: x = 30; y = 10; z = 50
EJERCICIO M1BE2292:
Juan, Pedro y Luis corren a la vez en un circuito. Por cada kilómetro que recorre Juan, Pedro recorre 2 kilómetros y Luis recorre tres cuartas partes de lo que recorre Pedro. Al finalizar, la suma de las distancias recorridas por los tres, fue de 45 kilómetros, ¿cuántos kilómetros recorrió cada uno?
SOLUCIÓN:
-
- x = «km que recorre Juan»
- y = «km que recorre Pedro»
- z = «km que recorre Luis»
-
-
- y = 2 x
- z = 3/4 y
- x + y + z = 45
-
Solución: x = 10; y = 20; z = 15