REGLA CRAMER MATEMÁTICAS SISTEMAS

DETERMINANTES DE ORDEN TRES

SISTEMAS DE ECUACIONES CONTEXTUALIZADOS

ÁLGEBRA. REGLA DE CRAMER PARA LA RESOLUCIÓN DE SISTEMAS DE ECUACIONES LINEALES:

ASPECTOS FORMALES LOMLOE PARA DOCENTES AL FINAL DEL ARTÍCULO

REGLA DE CRAMER DE RESOLUCIÓN DE SISTEMAS DE ECUACIONES:

Si tenemos un sistema de ecuaciones como el que se muestra, con tres ecuaciones y tres incógnitas

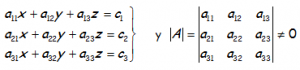
Los valores de x, y, z, se puede obtener realizando las siguientes operaciones con los determinantes asociados:

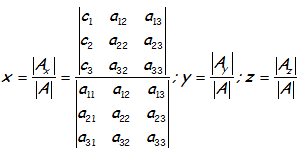
Notar como |A| es el determinante formado con los coeficientes de las incógnitas ordenadas.

|A_x| es el determinante que resulta de cambiar en el determinante de A la columna de las «x», por la columna de los términos independientes.

|A_y| es el determinante que resulta de cambiar en el determinante de A la columna de las «y», por la columna de los términos independientes, lo mismo para el determinante |A_z|.

Al igual que lo hemos tratado con tres ecuaciones y tres incógnitas, sería lo mismo con cuatro ecuaciones y cuatro incógnitas, o incluso con dos.

CÁLCULO DE DETERMINANTES DE ORDEN TRES:

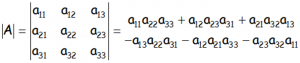
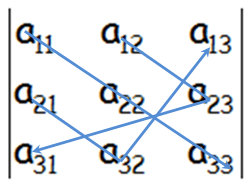
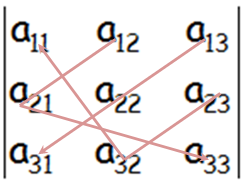
Donde debemos notar que hay seis términos, tres positivos y tres negativos, que se indican en azul o en rojo, respectivamente. Lo anterior para el cálculo del determinante de orden tres es la Regla de Sarrus.

- - En azul, los términos positivos, correspondientes a la diagonal principal y paralelas.
  - En rojo, los términos negativos, correspondientes a la diagonal secundaria y paralelas.

EJERCICIO M1BE2076:

Resolver el siguiente determinante:

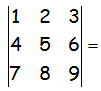
VÍDEO CON EL CÁLCULO DEL DETERMINANTE: https://youtu.be/QMiqgsi9Jr4

EJERCICIO M2BE1958:

Resolver el siguiente sistema de ecuaciones, utilizando la regla de Cramer:

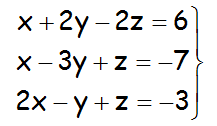
VÍDEO CON LA SOLUCIÓN DEL SISTEMA: https://youtu.be/9FYjSgcr-XM

EJERCICIO M1BE2141:

Un kiosco vende periódicos, libros y revistas. Los periódicos se venden a 1€, las revistas a 5€ y los libros a 12€. El importe total de las ventas realizadas la semana pasada ascendió a 1500 €. Por cada 3 revistas se vendieron 10 periódicos, y el importe de la venta de libros fue igual a la cuarta parte del importe total de las ventas de periódicos y revistas.

a) Plantear el correspondiente sistema de ecuaciones.

b) Resolver el sistema anterior: ¿cuántos libros, periódicos y revistas vendió el kiosco la semana pasada?

IR AL ARTÍCULO CON LA SOLUCIÓN DE ESTE SISTEMA DE ECUACIONES 3X3: PRUEBA DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS 1º BACHILLERATO

EJERCICIO M1BE2306:

Andrea, Regina y Carlota van a hacer un regalo a una amiga común. El regalo les cuesta 240 €. Como no todas disponen del mismo dinero, deciden pagar de la siguiente manera:

Andrea paga el triple de lo que pagan Regina y Carlota juntas, y por cada 0,12 € que paga Regina, Carlota paga 0,18 €.

Plantea un sistema que permita determinar cuánto paga cada persona y resuelve el problema.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE SISTEMA DE TRES ECUACIONES CON TRES INCÓGNICAS POR LA REGLA DE CRAMER

EJERCICIO M1BE2341:

En las Olimpiadas de Matemáticas, los seres humanos con mayor puntuación son: Mito, Lito y Tito, todos estudiantes del CPES Nuestra Señora del Pilar. Los tres acumulan 17500 puntos. Además, lo que ha anotado Tito más 2500 puntos es equivalente a la mitad de lo anotado por Mito. Finalmente, Lito anotó el doble que Tito. ¿Cuál es el ranking de puntuaciones de Mito, Lito y Tito?

IR A LA RESOLUCIÓN DE ESTE SISTEMA DE ECUACIONES LINEALES

EJERCICIO M2CCSSBE3073:

Una casa rural adquirió un total de 200 toallas de tres tipos: toallas de baño, toallas para manos y toallas para pies, gastando para ello un total de 7.600 euros. El precio de una toalla de baño es de 50 euros, el de una toalla para manos es de 40 euros y el de una toalla para pies es de 25 euros. Además, por cada tres toallas para manos se compraron dos toallas para pies. ¿Cuántas toallas de cada tipo ha comprado la casa rural?

IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN RESUELTO MATEMÁTICAS II CCSS. 2º DE BACHILLERATO. TERCER TRIMESTRE PRUEBA 1 DEL CURSO 2024-25.

EJERCICIO M1BE2077:

Durante una hora, una agencia de viajes vende un total de 30 billetes de avión con destino a las islas de La Palma, Gran Canaria y Lanzarote. Sabiendo que los billetes para Gran Canaria representan el doble de los emitidos para las otras dos islas, y que los correspondientes a Lanzarote son la mitad de los emitidos para La Palma más cuatro:

a) Plantear el correspondiente sistema de ecuaciones.

b) Determinar el número de billetes para cada una de las tres islas.

EJERCICIO M1BE2078:

En un crucero hay paquetes de tres tipos: individual (1 pasajero), pareja (2 pasajeros) y grupo familiar (4 pasajeros).

La tarifa individual es de 800 €, la tarifa de pareja es de 1200 € y la tarifa familiar es de 1600 €.

Para el próximo viaje hay 2400 pasajeros que han pagado un total de 1264000 €.

Si los pasajeros de individual son el 20% de la suma de los de pareja y de grupo familiar*,

a) Plantear el sistema de ecuaciones para determinar cuántos paquetes de cada tipo integran el crucero.

*NOTA: Prestar especial atención, hay detalles que tenemos que tener en cuenta.

b) Determinar la distribución de los pasajeros en los tres tipos de tarifa.

EJERCICIO M1BE2082 (EBAU CANARIAS 2021):

En la liga Mate-Basket, las mujeres matemáticas con mayor puntuación son: Lovelace, Noerther y Germain. Las tres acumulan 17500 puntos. Además, lo que ha anotado Germain más 2500 puntos es equivalente ala mitad de lo anotado por Lovelace. Finalmente, Noerther anotó el doble que Germain. ¿Cuál es el ranking de puntuaciones de la liga Mate-Basket de las jugadoras Lovelace, Noerther y Germain?

EJERCICIO M1BE2083 (EBAU CANARIAS 2021):

Un granjero compra un determinado mes 274€ de pienso para su ganado. Con ese dinero obtiene un total de 66 sacos de pienso de tres marcas diferentes: A, B y C. Se sabe que el precio de cada marca de pienso que ha comprado esde5€, 4€ y 4€, respectivamente. También se sabe que el número de sacos adquiridos de la marca C es el doble que el total de sacos comprados de las marcas A y B juntos. Averiguar la cantidad de sacos que el granjero ha comprado de cada una de las tres marcas.

EJERCICIO M1BE2084 (EBAU CANARIAS 2020):

Una pequeña bombonería tiene en su almacén 24 kg de chocolate y 60 litros de leche, con los que elabora tres productos distintos: cajas de bombones, tabletas de chocolate y paquetes de chocolate en polvo. Del resto de los ingredientes se tienen reservas suficientes. Se sabe que las cajas de bombones requieren 2kg de chocolate y 6 litros de leche, las tabletas de chocolate requieren4 kg de chocolate y 4 litros de leche, y cada paquete de chocolate en polvo requiere 1 kg de chocolate y 4 litros de leche. Se quiere fabricar un total de 12 unidades y con ello se consume todo el chocolate y toda la leche almacenados. ¿Cuántas unidades deben fabricarse de cada tipo de producto?

EJERCICIO M2BE2126:

Los precios de las entradas para un musical son 8 euros para los asistentes menores de 18 años, 25 euros para los adultos de menos de 60 años, y 10 euros para aquellos de al menos 60 años. Tras el concierto, se sabe que se han vendido tantas entradas de 25 euros como de las otras dos categorías juntas; y también que ha habido 9 asistentes menores de edad por cada uno de aquellos de al menos 60 años. Si la recaudación final fue de 8300 euros, calcular el número de asistentes de cada rango de edad.

EJERCICIO M2BE2256:

Un conocido defraudador fiscal tiene distribuido su dinero negro en tres paraísos fiscales, las Islas Caimán, Panamá y Fiji.

La suma total de este dinero es de 150 millones de euros. Si perdiera la cuarta parte del dinero que tiene en las Islas Caimán, seguiría teniendo allí el triple del dinero que tiene en Panamá. Además, el dinero que tiene en Panamá sumado a las dos quintas partes del dinero que tiene en Fiji es exactamente la mitad del dinero que tiene en las Islas Caimán.

Calcule cuánto dinero tiene en cada uno de los paraísos fiscales.

IR AL ENLACE CON LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN MATEMÁTICAS II 2º BACHILLERATO. CONVOCATORIA EXTRAORDINARIA

EJERCICIO M2BE2257:

En una estantería de una biblioteca hay ensayos, novelas y biografías. Tres de cada dieciséis libros de la estantería son ensayos. Las biografías junto con la tercera parte de los ensayos exceden en dos a las novelas. Si se retiraran la mitad de los ensayos y la quinta parte de las novelas quedarían ciento cinco libros.

Calcule el número de libros de cada clase que hay en la estantería.

EJERCICIO M2BE2260:

La suma de las edades de Carmela, Esperanza y Aurora es 68 años. La edad de Carmela es 5 años más que la mitad de la suma de las edades de Esperanza y Aurora. Además, dentro de 4 años la edad de Aurora será la edad que actualmente tiene Esperanza. Calcular las edades de cada una de ellas.

EJERCICIO M1BE2285:

En un grupo de 225 personas, el número de personas sin estudios es igual a la quinta parte de los que tienen estudios primarios. Si por cada 5 personas con estudios primarios hay 3 con estudios secundarios:

a) ¿Cuál es el sistema de ecuaciones que permite calcular el número de personas del grupo por nivel de estudios?

b) ¿Cuántas personas hay de cada nivel?

EJERCICIO M1BE2286:

Entre los tres trabajadores activos de una familia, madre, padre y hermano mayor, han ganado un total de 66000 euros. Si la madre gana el 125% de lo que gana el padre y las ganancias conjuntas de padre y hermano mayor igualan la suma de lo que gana la madre más la mitad de lo que gana el padre.

a) Plantear el sistema correspondiente.

b) ¿Cuánto gana cada uno?

EJERCICIO M1BE2287:

Se gastan 3031,25 euros en comprar 1000 cajas de papel de tres colores diferentes: amarillo, blanco y celeste.

La caja de papel amarillo cuesta 5,50 euros, la caja de papel blanco cuesta 3,75 euros y, como es reutilizado, la caja de papel celeste cuesta 2,25 euros. Sabiendo que el número de cajas celestes es el número de cajas amarillas más el doble del número de cajas blancas. Se pide:

a) Plantear el sistema que permita hallar la cantidad de cajas de cada tipo que se han comprado.

b) Resolver dicho sistema.

EJERCICIO M1BE2288:

Una agencia de viajes ha vendido un total de 128 cruceros de los tipos Alegría, Belleza y Concordia, cuyos precios por persona son 1500, 600 y 900 euros, respectivamente, recaudando 112800 euros.

Si por cada persona que va al crucero Alegría hay dos que van al crucero Concordia.

a) Plantear el correspondiente sistema de ecuaciones.

b) ¿Cuántas personas van a cada tipo de crucero?

EJERCICIO M1BE2289:

En un cine de Suiza se proyectan las películas en tres lenguas: alemán, italiano y francés. El número total de proyecciones es 2000 y, debido a la composición de la población suiza, se hacen siguiendo las siguientes normas:

– El 60% de las películas en italiano más el 50% de las películas en francés hacen las dos terceras partes de las proyecciones en alemán.

– Por cada dos proyecciones en francés se hacen 3 proyecciones en alemán.

a) Plantear el correspondiente sistema de ecuaciones.

b) Calcular cuántas proyecciones se hacen en cada una de las lenguas.

EJERCICIO M1BE2290:

En un grupo hay 288 personas de entre 18 y 25 años clasificados como estudiantes, empleados y sin ocupación. Por cada cinco estudiantes hay tres empleados y los sin ocupación representan el 80% del resto.

a) Plantear el correspondiente sistema de ecuaciones.

b) ¿Cuántos estudiantes, empleados y sin ocupación hay?

EJERCICIO M1BE2291:

Se tienen que empaquetar 1500 unidades de un artículo en cajas de 5, 10 y 25 unidades, de manera que haya el triple de cajas de 5 unidades que de 10 unidades y que el número total de cajas sea igual a 90. ¿Cuántas cajas tiene que haber de cada tipo?

EJERCICIO M1BE2292:

Juan, Pedro y Luis corren a la vez en un circuito. Por cada kilómetro que recorre Juan, Pedro recorre 2 kilómetros y Luis recorre tres cuartas partes de lo que recorre Pedro. Al finalizar, la suma de las distancias recorridas por los tres, fue de 45 kilómetros, ¿cuántos kilómetros recorrió cada uno?

EJERCICIO M1BE2293:

Una empresa de juguetes fabrica bicicletas, triciclos y coches en los que utiliza un mismo modelo de ruedas. Se sabe que, en los 280 juguetes que va a fabricar, se necesitan 945 ruedas. Si se van a producir 10 bicicletas menos que triciclos.

a) ¿Cuántos coches, bicicletas y triciclos se fabricarán?

b) Si las bicicletas se venden a 65€, los triciclos a 75€ y los coches a 90€, ¿cuál es el valor total de los juguetes producidos?

EJERCICIO M1BE2294:

La edad, en años, de Juan es el doble que la suma de las edades de sus dos hijos: Pedro y Luis. A su vez, Pedro es 3 años mayor que Luis. Si, dentro de 10 años, la edad del padre sobrepasa en 11 años a la suma de las edades de los hijos:

a) Plantear el correspondiente sistema de ecuaciones.

b) Determinar la edad de cada uno de ellos.

EJERCICIO M1BE2295:

En una competición escolar participan 1500 niños de tres categorías: alevines, infantiles y juveniles. Se sabe que los juveniles son el doble de los alevines y que, sumados los alevines e infantiles, hay 100 menos que juveniles. ¿Cuántos hay de cada categoría?

EJERCICIO M1BE2296:

Un agricultor compra semillas de garbanzos 1,30 € el kilo, de alubias a 1,20 € el kilo y de lentejas a 0,80 € el kilo. En total compra 45 kilos de semillas y paga por ellas 43 €. Sabiendo que el peso de las lentejas es el doble que lo que pesan, conjuntamente, los garbanzos y las alubias, calcular qué cantidad de semillas ha comprado de cada legumbre.

IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS I, 1º BACHILLERATO CIENCIAS Y TECNOLOGÍA, DE ARITMÉTICA Y ÁLGEBRA

EJERCICIO M1BE2938:

Una tienda de informática vende pendrives de 32 Gb, 64 Gb y 128 Gb, siendo sus precios 5 €, 15 € y 20 €, respectivamente. Un cliente ha comprado un total de 15 pendrives que le han costado 160 €. Sabiendo que el número de pendrives de 128 Gb que compró era la cuarta parte del resto.

a) Plantear el correspondiente sistema de ecuaciones.

b) Calcular cuántos pendrives de cada clase compró el cliente.

IR AL ARTÍCULO CON LA SOLUCIÓN DE ESTE SISTEMA DE ECUACIONES CONTEXTUALZADO 3X3: EXAMEN RESUELTO DE ECUACIONES, SISTEMAS Y NÚMEROS COMPLEJOS PARA MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA

EJERCICIO M1BE2895:

Un avión ofrece asientos de tres clases: primera, preferente y turista. El número de asientos de la clase preferente son el doble que los de primera clase, y por cada 15 asientos de clase turista hay dos de clase preferente. El precio por asiento fue de 350€ para primera clase, 280€ para clase preferente y 200€ para la clase turista. Si el importe total cobrado por los asientos fue de 31280€, ¿cuántos asientos de cada clase había en el avión?

IR AL ARTÍCULO CON LA SOLUCIÓN DE ESTE SISTEMA DE ECUACIONES: PRUEBA DE EXAMEN RESUELTA DE MATEMÁTICAS I, DE 1º BACHILLERATO. ARITMÉTICA Y ÁLGEBRA. NÚMEROS COMPLEJOS

ASPECTOS FORMALES:

SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS: