EXAMEN ÁLGEBRA ARITMÉTICA BACHILLERATO
MATEMÁTICAS I 1º BACHILLERATO CIENCIAS
EXAMEN RESUELTO PASO A PASO DE ÁLGEBRA Y ARITMÉTICA PARA MATEMÁTICAS DE 1º DE BACHILLERATO (X662), REALIZADO EN «EL PILAR»:

PRUEBA EVALUADORA QUE INCLUYE SABERES BÁSICOS DE MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS RELATIVOS A:
-
- LOS NÚMEROS COMPLEJOS. ARITMÉTICA Y ÁLGEBRA PARA BACHILLERATO.
- MATERIALES DE ÁLGEBRA PARA 1º DE BACHILLERATO
- Ecuaciones exponenciales
- SISTEMAS DE ECUACIONES EXPONENCIALES
- Ecuaciones polinómicas de grado superior a dos
- Ecuaciones con denominadores algebraicos
- REGLA DE CRAMER. SISTEMAS DE ECUACIONES PARA BACHILLERATO
MÁS RECURSOS DISPONIBLES PARA MATEMÁTICAS DE 1º DE BACHILLERATO: MATEMÁTICAS 1º DE BACHILLERATO
SIGUE EL PROCESO DETERMINADO SEGÚN: MATEMÁTICAS I DE 1º DE BACHILLERATO: DESARROLLO DE LA ASIGNATURA
ESTA PRUEBA SE REALIZA CON LA «DINÁMICA DEL DÍA DESPUÉS», EN LA QUE AL DÍA SIGUIENTE DE LA PRUEBA SE LES ENTREGA A LOS ALUMNOS LOS ENUNCIADOS DE LA PRUEBA Y SE LES PERMITE QUE ELIJAN UNA DE LAS PREGUNTAS DE LA PRUEBA, LA HAGAN DE NUEVO, DISPONIENDO DE 10 MINUTOS CRONOMETRADOS, Y SUSTITUIRÁ A LA REALIZADA. TAL ESTRATEGIA MOTIVA EN LOS ALUMNOS LA REFLEXIÓN DE LO REALIZADO CON POSTERIORIDAD A LA PRUEBA, SIENDO UNA DINÁMICA QUE REFUERZA LA COMPETENCIA APRENDER A APRENDER Y MEJORA LOS RESULTADOS DE LOS ALUMNOS QUE CON INTERÉS REALIZAN UNA REFLEXIÓN DE LO QUE HAN TRABAJADO EN LA PRUEBA, CONTRASTANDO LO QUE HAN PUESTO CON SUS APUNTES Y/O COMPAÑEROS.
LOS ENUNCIADOS DE ESTA PRUEBA DE ÁLGEBRA Y ARITMÉTICA PARA 1º DE BACHILLERATO:
X662 EXAMEN ÁLGEBRA ARITMÉTICA MATEMÁTICAS 1º BAC 23 24_v1LOS EJERCICIOS DE LA PRUEBA Y SU RESOLUCIÓN PASO A PASO:
EJERCICIO M1BE2341:
En las Olimpiadas de Matemáticas, los seres humanos con mayor puntuación son: Mito, Lito y Tito, todos estudiantes del CPES Nuestra Señora del Pilar. Los tres acumulan 17500 puntos. Además, lo que ha anotado Tito más 2500 puntos es equivalente a la mitad de lo anotado por Mito. Finalmente, Lito anotó el doble que Tito. ¿Cuál es el ranking de puntuaciones de Mito, Lito y Tito?
LA RESOLUCIÓN PASO A PASO DE ESTE PROBLEMA DE SISTEMAS DE ECUACIONES:
EJERCICIO M1BE2341 SISTEMA ECUACIONES CRAMER_v1EJERCICIO M1BE2342:
Calcular el parámetro k para que el siguiente número complejo sea real:
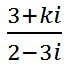
LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE NÚMEROS COMPLEJOS:
EJERCICIO M1BE2342 NÚMEROS COMPLEJOS_v1EJERCICIO M1BE2330:
Resolver la siguiente ecuación trigonométrica:
sen 3x + sen 6x =0
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/5TxbbFoXYd8
CAPTURAS DEL VÍDEO PARA UN CONTRASTE INMEDIATO DE LO REALIZADO:
EJERCICIO M1BE2330 ECUACIÓN TRIGONOMÉTRICA
EJERCICIO M1BE2343:
Resolver la siguiente ecuación racional:
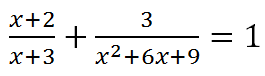
LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN RACIONAL:
EJERCICIO M1BE2343 ECUACIÓN RACIONAL_v1EJERCICIO M1BE2344:
Resolver la siguiente ecuación exponencial:
![]()
LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN EXPONENCIAL:
EJERCICIO M1BE2344 ECUACIÓN EXPONENCIAL 2_v1EJERCICIO M1BE2345:
Resolver la siguiente ecuación polinómica:
![]()
LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN POLINÓMICA:
EJERCICIO M1BE2345 ECUACIÓN POLINÓMICA_v1EJERCICIO M1BE2346:
Resolver el siguiente sistema de ecuaciones:
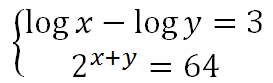
LA RESOLUCIÓN PASO A PASO DE ESTE SISTEMA DE ECUACIONES:
EJERCICIO M1BE2346 SISTEMA ECUACIONES LOGARITMICAS_v1EJERCICIO M1BE2347:
Resolver la siguiente ecuación logarítmica:
![]()
LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN LOGARÍTMICA:
EJERCICIO M1BE2347 ECUACIÓN LOGARÍTMICA_v1
