MATERIALES ÁLGEBRA MATEMÁTICAS BACHILLERATO
ECUACIONES
MATERIALES DE ÁLGEBRA PARA MATEMÁTICAS DE 1º DE BACHILLERATO:
Pretendemos que éste sea el artículo de referencia para los contenidos de Álgebra de Matemáticas de 1º de Bachillerato. Algunos son contenidos de repaso/profundización de la etapa anterior y otros son específicos de esta nueva etapa:
LOS ASPECTOS FORMALES, PARA DOCENTES, AL FINAL DE ESTE MISMO ARTÍCULO
ECUACIONES DE SEGUNDO GRADO:
Expresión general y aclaraciones, para la resolución de ecuaciones de 2º grado y ejercicio resuelto,
EJERCICIO M4EE2331:
Resolver la siguiente ecuación:
x2 + 5x + 6 = 0
VÍDEO QUE RESUELVE LA ECUACIÓN: https://youtu.be/i52d9dZyJ0w?si=GsjG-AWLllK5U1cF
EJERCICIO M4EE2332:
Resolver las siguientes ecuaciones de 2º grado:
a.- x2 – 36 = 0
b.- 2x2 – 50 = 0
c.- x2 + 3x = 0
d.- x2 – x = 0
VÍDEO QUE RESUELVE ESTAS ECUACIONES DE SEGUNDO GRADO INCOMPLETAS: https://youtu.be/dGf7CkZxndw?si=Al8fUZII6RqVE8TN
EJERCICIO M4EE2872:
Resolver la siguiente ecuación:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN IRRACIONAL: EXAMEN RESUELTO DE MATEMÁTICAS DE 4º DE LA E.S.O., DE ECUACIONES Y SISTEMAS DE ECUACIONES
ECUACIONES POLINÓMICAS DE GRADO SUPERIOR A DOS:
EJERCICIO M1BE2052:
a.- Descomponer en factores el siguiente polinomio: P(x) = x3 – 4x2 + x + 6
b.- Resolver la ecuación: x3 – 4x2 + x + 6 = 0
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/uJ_DgrNgorI
EJERCICIO M1BE2136:
Resolver la siguiente ecuación polinómica:
x4 – x2 – 6x = 0
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: PRUEBA DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS 1º BACHILLERATO
EJERCICIO M1BE2306b:
Resolver la siguiente ecuación:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN POLINÓMICA
EJERCICIO M1BE2311:
Resolver la siguiente ecuación:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN POLINÓMICA
EJERCICIO M1BE2304:
Resolver:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN DE SEGUNDO GRADO
EJERCICIO M1BE2324:
Resolver la siguiente ecuación, pero dando todas las soluciones correspondientes a la misma:
(3x-2)2 = (x+6)2
IR A LA RESOLUCIÓN DE ESTA ECUACIÓN POLINÓMICA
EJERCICIO M1BE2345:
Resolver la siguiente ecuación polinómica:
IR A LA RESOLUCIÓN DE ESTA ECUACIÓN POLINÓMICA
EJERCICIO M1BE2599:
Resolver la siguiente ecuación y comprobar los resultados cuando sea necesario para confirmar que son solución:
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN: EXAMEN INICIAL RESUELTO DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS I, DE 1º DE BACHILLERATO. CURSO 2024-25
EJERCICIO M1BE2600:
Resolver la siguiente ecuación y comprobar los resultados cuando sea necesario para confirmar que son solución:
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN: EXAMEN INICIAL RESUELTO DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS I, DE 1º DE BACHILLERATO. CURSO 2024-25
EJERCICIO M4EE2866:
Resolver la siguiente ecuación:
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN: EXAMEN RESUELTO DE MATEMÁTICAS DE 4º DE LA E.S.O., DE ECUACIONES Y SISTEMAS DE ECUACIONES
EJERCICIO M4EE2868:
Resolver la siguiente ecuación:
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN: EXAMEN RESUELTO DE MATEMÁTICAS DE 4º DE LA E.S.O., DE ECUACIONES Y SISTEMAS DE ECUACIONES
EJERCICIO M1BE2861:
Resolver la siguiente ecuación, comprobar los resultados cuando sea necesario para confirmar que son solución:
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN: EXAMEN RESUELTO DE MATEMÁTICAS I, 1º BACHILLERATO CIENCIAS Y TECNOLOGÍA, DE ARITMÉTICA Y ÁLGEBRA
ECUACIONES CON DENOMINADORES:
EJERCICIO M4EE2865:
Resolver la siguiente ecuación:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN CON DENOMINADORES NUMÉRICOS: EXAMEN RESUELTO DE MATEMÁTICAS DE 4º DE LA E.S.O., DE ECUACIONES Y SISTEMAS DE ECUACIONES
ECUACIONES CON DENOMINADORES ALGEBRAICOS. ECUACIONES RACIONALES:
EJERCICIO M1BE2137:
Resolver la siguiente ecuación con denominadores algebraicos:
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: PRUEBA DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS 1º BACHILLERATO
EJERCICIO M1BE2285:
Resolver la siguiente ecuación y comprobar los resultados cuando sea necesario para confirmar que son solución:
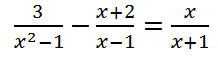
IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ECUACIONES CON DENOMINADORES ALGEBRAICOS
EJERCICIO M1BE2309:
Resolver la siguiente ecuación:
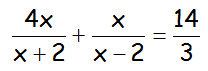
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN CON DENOMINADORES ALGEBRAICOS
EJERCICIO M1BE2343:
Resolver la siguiente ecuación racional:
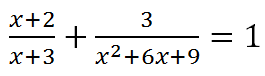
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN RACIONAL
EJERCICIO M1BE2601:
Resolver la siguiente ecuación y comprobar los resultados cuando sea necesario para confirmar que son solución:
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN: EXAMEN INICIAL RESUELTO DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS I, DE 1º DE BACHILLERATO. CURSO 2024-25
EJERCICIO M1BE2932:
Resolver la siguiente ecuación:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN RACIONAL: EXAMEN RESUELTO DE ECUACIONES, SISTEMAS Y NÚMEROS COMPLEJOS PARA MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA
EJERCICIO M1BE2890:
Resolver la siguiente ecuación, comprobando las soluciones si fuera necesario:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN RACIONAL: PRUEBA DE EXAMEN RESUELTA DE MATEMÁTICAS I, DE 1º BACHILLERATO. ARITMÉTICA Y ÁLGEBRA. NÚMEROS COMPLEJOS
EJERCICIO M4EE2869:
Resolver la siguiente ecuación:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN IRRACIONAL: EXAMEN RESUELTO DE MATEMÁTICAS DE 4º DE LA E.S.O., DE ECUACIONES Y SISTEMAS DE ECUACIONES
EJERCICIO M4EE2871:
Resolver la siguiente ecuación:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN IRRACIONAL: EXAMEN RESUELTO DE MATEMÁTICAS DE 4º DE LA E.S.O., DE ECUACIONES Y SISTEMAS DE ECUACIONES
ECUACIONES IRRACIONALES:
EJERCICIO M1BE1964:
Resolver la siguiente ecuación irracional:
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/jcqIm8Sn_Ew
EJERCICIO M1BE2054:
Resolver la siguiente ecuación irracional:
VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/3PnfJgMU5lQ
EJERCICIO M1BE2055:
Resolver la siguiente ecuación irracional:
VÍDEO CON LA SOLUCIÓN DE LA ECUACIÓN: https://youtu.be/C2SUQyP-5-Y
EJERCICIO M1BE2598:
Resolver la siguiente ecuación y comprobar los resultados cuando sea necesario para confirmar que son solución:
IR AL ARTÍCULO CON LA RESOLUCIÓN DE ESTA ECUACIÓN: EXAMEN INICIAL RESUELTO DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS I, DE 1º DE BACHILLERATO. CURSO 2024-25
EJERCICIO M1BE2135:
Resolver la siguiente ecuación irracional:
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: PRUEBA DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS 1º BACHILLERATO
EJERCICIO M1BE2281:
Resolver la siguiente ecuación y comprobar los resultados cuando sea necesario para confirmar que son solución:
IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ECUACIÓN IRRACIONALES
EJERCICIO M1BE2284:
Resolver la siguiente ecuación y comprobar los resultados cuando sea necesario para confirmar que son solución:
IR A LA SOLUCIÓN PASO A PASO DE ESTA ECUACIÓN IRRACIONAL
EJERCICIO M1BE2310b:
Resolver la siguiente ecuación:
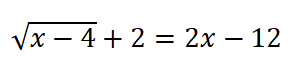
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN IRRACIONAL
EJERCICIO M1BE2933:
Resolver la siguiente ecuación:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN IRRACIONAL: EXAMEN RESUELTO DE ECUACIONES, SISTEMAS Y NÚMEROS COMPLEJOS PARA MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA
EJERCICIO M1BE2891:
Resolver la siguiente ecuación, comprobando las soluciones si fuera necesario:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN IRRACIONAL: PRUEBA DE EXAMEN RESUELTA DE MATEMÁTICAS I, DE 1º BACHILLERATO. ARITMÉTICA Y ÁLGEBRA. NÚMEROS COMPLEJOS
EJERCICIO M4EE2867:
Resolver la siguiente ecuación:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN IRRACIONAL: EXAMEN RESUELTO DE MATEMÁTICAS DE 4º DE LA E.S.O., DE ECUACIONES Y SISTEMAS DE ECUACIONES
EJERCICIO M1BE2859:
Resolver la siguiente ecuación, comprobar los resultados cuando sea necesario para confirmar que son solución:
IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE MATEMÁTICAS I, 1º BACHILLERATO CIENCIAS Y TECNOLOGÍA, DE ARITMÉTICA Y ÁLGEBRA
ECUACIONES LOGARÍTMICAS:
TENER MUY PRESENTE LAS PROPIEDADES DE LOS LOGARITMOS ÚTILES EN ECUACIONES LOGARÍTMICAS:
EJERCICIO M1BE1962:
Resolver la siguiente ecuación logarítmica:
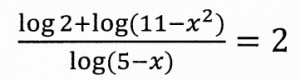
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/WWC0m8V6ooY
EJERCICIO M1BE2134:
Resolver la siguiente ecuación logarítmica:
log (3x-1) -log (2x+3) = 1 – log 25
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: PRUEBA DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS 1º BACHILLERATO
EJERCICIO M1BE2313:
Resolver la siguiente ecuación:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN LOGARÍTMICA
EJERCICIO M1BE2309b:
Resolver la siguiente ecuación:
log x + log (x+9) =1
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN LOGARÍTMICA
EJERCICIO M1BE2327:
Resolver la siguiente ecuación:
(log5 x)2 – log5 x2 = – 1
IR A LA RESOLUCIÓN DE ESTA ECUACIÓN LOGARÍTMICA
EJERCICIO M1BE2329:
Resolver la siguiente ecuación:
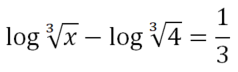
IR A LA RESOLUCIÓN DE ESTA ECUACIÓN LOGARÍTMICA
EJERCICIO M1BE2347:
Resolver la siguiente ecuación logarítmica:
IR A LA RESOLUCIÓN DE ESTA ECUACIÓN LOGARÍTMICA
EJERCICIO M1BE2934:
Resolver la siguiente ecuación:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN LOGARÍTMICA: EXAMEN RESUELTO DE ECUACIONES, SISTEMAS Y NÚMEROS COMPLEJOS PARA MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA
EJERCICIO M1BE2892:
Resolver la siguiente ecuación, comprobando las soluciones si fuera necesario:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN LOGARÍTMICA: PRUEBA DE EXAMEN RESUELTA DE MATEMÁTICAS I, DE 1º BACHILLERATO. ARITMÉTICA Y ÁLGEBRA. NÚMEROS COMPLEJOS
ECUACIONES EXPONENCIALES:
TENER MUY PRESENTE LAS PROPIEDADES DE LAS POTENCIAS:
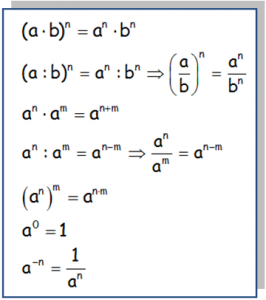
EJERCICIO M1BE1963:
Resolver la siguiente ecuación exponencial:
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/h70OmZ7DNk0
EJERCICIO M1BE2133:
Resolver la siguiente ecuación exponencial:
IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: PRUEBA DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS 1º BACHILLERATO
EJERCICIO M1BE2286:
Resolver la siguiente ecuación y comprobar los resultados cuando sea necesario para confirmar que son solución:
IR A LA SOLUCIÓN PASO A PASO DE ESTA ECUACIÓN EXPONENCIAL
EJERCICIO M1BE2282 Y M1BE2283:
Resolver las siguiente ecuaciones y comprobar los resultados cuando sea necesario para confirmar que son solución:
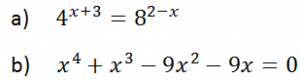
IR A LA SOLUCIÓN PASO A PASO DE ESTAS ECUACIONES
EJERCICIO M1BE2310:
Resolver la siguiente ecuación:
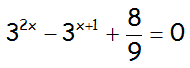
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN EXPONENCIAL
EJERCICIO M1BE2307b:
Resolver la siguiente ecuación:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN EXPONENCIAL
EJERCICIO M1BE2311b:
Resolver la siguiente ecuación:
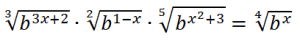
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN EXPONENCIAL
EJERCICIO M1BE2326:
Resolver la siguiente ecuación:
9x – 2·6x = – 4x
IR A LA RESOLUCIÓN DE ESTA ECUACIÓN EXPONENCIAL
EJERCICIO M1BE2328:
Resolver la siguiente ecuación:
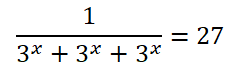
IR A LA RESOLUCIÓN DE ESTA ECUACIÓN EXPONENCIAL
EJERCICIO M1BE2344:
Resolver la siguiente ecuación exponencial:
IR A LA RESOLUCIÓN DE ESTA ECUACIÓN EXPONENCIAL
EJERCICIO M1BE2931:
Resolver la siguiente ecuación:
IR A LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN EXPONENCIAL: EXAMEN RESUELTO DE ECUACIONES, SISTEMAS Y NÚMEROS COMPLEJOS PARA MATEMÁTICAS DE 1º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA
EJERCICIO M1BE2889:
Resolver la siguiente ecuación, comprobando las soluciones si fuera necesario:
IR AL ARTÍCULO CON LA RESOLUCIÓN PASO A PASO DE ESTA ECUACIÓN EXPONENCIAL: PRUEBA DE EXAMEN RESUELTA DE MATEMÁTICAS I, DE 1º BACHILLERATO. ARITMÉTICA Y ÁLGEBRA. NÚMEROS COMPLEJOS
ECUACIONES CON SOLUCIONES COMPLEJAS:
INTERESA IR A LOS NÚMEROS COMPLEJOS. ARITMÉTICA Y ÁLGEBRA PARA BACHILLERATO.
EJERCICIO M1BE2060:
Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera, expresadas en forma binómica:
x2 – 2x + 4 = 0
Comprobar con alguna de las soluciones, que realmente lo es.
VÍDEO QUE SOLUCIONA LA ECUACIÓN: https://youtu.be/TTgx9-6Kzjg
EJERCICIO M1BE2065:
Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:
x3 – 1 = 0
NOTA: TENER EN CUENTA QUE UNA ECUACIÓN DE TERCER GRADO, POSIBLEMENTE TENGA TRES SOLUCIONES, QUE ALGUNA O ALGUNAS PODRÍAN SER COMPLEJAS.
EJERCICIO M1BE2066:
Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:
x3 + 1 = 0
NOTA: TENER EN CUENTA QUE UNA ECUACIÓN DE TERCER GRADO, POSIBLEMENTE TENGA TRES SOLUCIONES, QUE ALGUNA O ALGUNAS PODRÍAN SER COMPLEJAS.
SISTEMAS DE ECUACIONES:
EJERCICIO M1BE2305:
Resolver el siguiente sistema de ecuaciones:
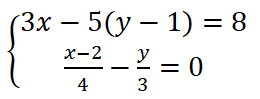
IR A LA RESOLUCIÓN PASO A PASO DE ESTE SISTEMA DE ECUACIONES
SISTEMAS DE ECUACIONES EXPONENCIALES Y LOGARÍTMICOS:
EJERCICIO M1BE1965:
Resolver el siguiente sistema, de ecuaciones exponenciales:
VÍDEO QUE RESUELVE EL EJERCICIO: https://youtu.be/ANOczmZO548
EJERCICIO M1BE2346:
Resolver el siguiente sistema de ecuaciones:
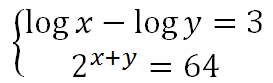
IR A LA RESOLUCIÓN DE ESTE SISTEMA DE ECUACIONES LOGARÍTMICO-EXPONENCIAL
PUEDEN INTERESAR LOS SIGUIENTES ARTÍCULOS DE ESTE MISMO PROYECTO:
- ECUACIONES PELIGROSAS PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO
- SISTEMAS DE ECUACIONES LOGARÍTMICAS
- SISTEMAS DE ECUACIONES EXPONENCIALES
- RESOLUCIÓN DE SISTEMAS DE ECUACIONES DE NIVEL. FÍSICA BACHILLERATO
- ECUACIONES TRIGONOMÉTRICAS
EJERCICIOS DE ÁLGEBRA DE INTERÉS PARA MATEMÁTICAS DE 1º BACHILLERATO:
152 ALGEBRA 1BAC V4_2ASPECTOS FORMALES:
SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS:
- COMPETENCIA MATEMÁTICA Y EN CIENCIA, TECNOLOGÍA E INGENIERÍA (STEM), concretamente el DESCRIPTOR OPERATIVO STEM1.
- COMPETENCIA EN COMUNICACIÓN LINGÜÍSTICA (CLL), concretamente el DESCRIPTOR OPERATIVO CCL2.
- COMPETENCIA DIGITAL (CD), concretamente el DESCRIPTOR OPERATIVO CD1.
- COMPETENCIA PERSONAL, SOCIAL Y DE APRENDER A APRENDER (CPSAA), concretamente el DESCRIPTOR OPERATIVO CPSAA1.1
- COMPETENCIA EMPRENDEDORA (CE), concretamente el DESCRIPTOR OPERATIVO CE1
CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS I DE 1º DE BACHILLERATO
MATI1BAC1.1 , MATI1BAC1.2 , MATI1BAC2.1 , MATI1BAC2.2 , MATI1BAC3.1 , MATI1BAC4.1 , MATI1BAC5.1 , MATI1BAC5.2 , MATI1BAC6.1 , MATI1BAC6.2 , MATI1BAC7.1 , MATI1BAC7.2 , MATI1BAC8.1 , MATI1BAC8.2 , MATI1BAC9.1 , MATI1BAC9.2 , MATI1BAC9.3
SE OBSERVAN LAS COMPETENCIAS ESPECÍFICAS DE MATEMÁTICAS I Y II Y ESTÁN HIPERVINCULADOS A LOS DESCRIPTORES OPERATIVOS DE LAS COMPETENCIAS CLAVE
Comments are closed, but trackbacks and pingbacks are open.