RESOLUCIÓN DE SISTEMAS DE ECUACIONES DE NIVEL. FÍSICA BACHILLERATO

SISTEMAS ECUACIONES NIVEL FÍSICA

RESOLUCIÓN DE SISTEMAS DE ECUACIONES DE CIERTO NIVEL, CON ESTRATEGIAS CONVENIENTES PARA FÍSICA DE 2º DE BACHILLERATO:

ASPECTOS FORMALES PARA DOCENTES, ACTUALIZADOS A LA LOMLOE, AL FINAL DEL ARTÍCULO, PARA NO INTERFERIR CON LO QUE TIENE INTERÉS PARA EL APRENDIZAJE DE NUESTROS ALUMNOS.

En el Bachillerato, sobre todo en 2º de Bachillerato, todos sabemos resolver sistemas de ecuaciones: lineales de dos e incluso de 3 incógnitas, sistemas de ecuaciones exponenciales, logarítmicas, combinaciones de ellos y trigonométricos.

Conocemos el método de Cramer, el análisis de sistemas por el Teorema de Rouché, y sobre todo estamos muy puestos en… sustitución, igualación y reducción.

Queremos plantear aquí una estrategia que surgió en un examen de EBAU de Física, que pretendemos desde el proyecto Achimagec, abra nuestra mente a «ideas felices», que con frecuencia es necesario tener cuando aplicamos el álgebra en asignaturas de ciencias aplicadas, sobre todo en Física.

Comenzamos poniendo el enunciado del ejercicio que nos lleva a esta cuestión que abordamos, de la EBAU de Física Canarias, del contenido de Movimiento Ondulatorio:

EJERCICIO F2BEE2038:

Una onda sinusoidal transversal en una cuerda tiene un período de 0,2 s y se propaga en el sentido negativo del eje X a una velocidad de 30 m/s. En el instante t = 0, la partícula de la cuerda en x = 0 tiene una elongación negativa de 0,02 m y una velocidad de oscilación negativa de 2 m/s.

a) ¿Cuál es la amplitud de la onda?) ¿Y la fase inicial?

b) ¿Cuál es la velocidad de oscilación máxima de un punto de la cuerda?

c) Escriba la ecuación de la onda correspondiente.

El desarrollo del ejercicio se lo dejamos a los Físicos, el caso es que para resolver el primer apartado se obtiene, de la aplicación de las estrategias correctas, que además no son sencillas, las siguientes ecuaciones:

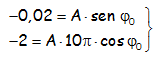
A es la amplitud, es una distancia, se mide en metros en el S.I.; φ₀ es la fase inicial, es un ángulo que se mide en radianes en el S.I., lo cual complica las cosas. Para colmo, es un sistema de ecuaciones trigonométricas serio: una de las incógnitas está sometida a dos funciones trigonométricas.

Sería fantástico que en el primer contacto con este sistema de ecuaciones para un alumno de bachillerato, se tomara su tiempo en pensar estrategias para resolverlo, y no continuara leyendo hasta pasado un rato.

Estamos muy acostumbrados a realizar sustituciones, igualaciones, todo ello es posible a través de la Amplitud… y otras estrategias, pero sin duda alguna, la mejor en este caso, a falta de algo mejor que proponga alguien es, la división de las dos ecuaciones.

Dividir las ecuaciones, no es una estrategia habitual que se haya realizado en cursos anteriores, pero en este caso es una «idea feliz» estupenda, bajo nuestro punto de vista. Veamos:

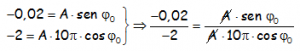
No sólo nos permite eliminar una incógnita, la Amplitud, sino que encima gracias a la definición de tangente, conseguimos cambiar las dos funciones trigonométricas por una sola:

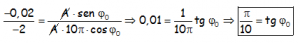
Con lo cual ya podemos calcular la fase inicial, teniendo en cuenta que tenemos que tener la calculadora en radianes:

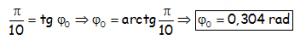
Hay que tener en cuenta que ese ángulo hay que revisarlo, ya que teniendo en cuenta que la amplitud es una cantidad positiva (ya que nos habla de la máxima elongación, tanto para arriba como para abajo), podría no corresponder al correcto.

De hecho, el seno del ángulo es negativo y el coseno también, con lo cual no corresponde con uno del primer cuadrante, sino con uno del tercer cuadrante, esto es π+0,304.

Una vez con este ángulo, se puede obtener el valor de la amplitud, que es de 0,067 m.

Tener lo anterior en cuenta: en Física, la división de ecuaciones, en algunos casos, es una estrategia «feliz» que nos puede ayudar a resolver situaciones matemáticas complicadas.

Ni que decir tiene, que es un proceso absolutamente legal desde el punto de vista matemático, ya que si:

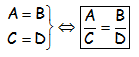
EJERCICIO F2BEE2543:

Una onda sinusoidal transversal en una cuerda tiene un período de 0,2 s y se propaga en el sentido negativo del eje X a una velocidad de 30 m/s. En el instante t = 0, la partícula de la cuerda en x = 0 tiene una elongación de +0,02 m y una velocidad de oscilación negativa de 2 m/s.

a) ¿Cuál es la amplitud de la onda?) ¿Y la fase inicial?

b) ¿Cuál es la velocidad de oscilación máxima de un punto de la cuerda?

c) Escriba la ecuación de la onda correspondiente.

EJERCICIO F2BEE2544:

Una onda sinusoidal transversal en una cuerda tiene un período de 0,2 s y se propaga en el sentido negativo del eje X a una velocidad de 30 m/s. En el instante t = 0, la partícula de la cuerda en x = 0 tiene una elongación de -0,02 m y una velocidad de oscilación de +2 m/s.

a) ¿Cuál es la amplitud de la onda?) ¿Y la fase inicial?

b) ¿Cuál es la velocidad de oscilación máxima de un punto de la cuerda?

c) Escriba la ecuación de la onda correspondiente.

EJERCICIO F2BEE2545:

Una onda sinusoidal transversal en una cuerda tiene un período de 0,2 s y se propaga en el sentido negativo del eje X a una velocidad de 30 m/s. En el instante t = 0, la partícula de la cuerda en x = 0 tiene una elongación de + 0,02 m y una velocidad de oscilación de + 2 m/s.

a) ¿Cuál es la amplitud de la onda?) ¿Y la fase inicial?

b) ¿Cuál es la velocidad de oscilación máxima de un punto de la cuerda?

c) Escriba la ecuación de la onda correspondiente.

EJERCICIO F2BE2564:

Una onda sinusoidal transversal que se desplaza en el sentido positivo del eje X, se propaga en un cable de acero, con una velocidad de 1,5 m/s, con un periodo de 2 segundos.

Se observa que en x=0 en el instante inicial su elongación es de -5 cm y la velocidad de vibración es de 0,05·π m/s,

a.- Hallar la amplitud y la fase inicial del movimiento ondulatorio.

b.- ¿Cuál sería la fase inicial si en x=0 en el instante inicial la elongación sigue siendo de -5 cm, pero la velocidad de vibración fuera negativa de valor -0,05 π m/s?

c.- Escribir la ecuación de la onda correspondiente a cada una de las situaciones planteadas en los dos apartados anteriores.

IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN FINAL FÍSICA 2º BACHILLERATO. EFECTO FOTOELÉCTRICO, ONDAS, ELECTROMAGNETISMO, GRAVITACIÓN, RELATIVIDAD, CUÁNTICA.

EJERCICIO F2BE2528:

En la superficie de una piscina de 7,5 m de largo, de estudio del efecto de los tsunamis, se genera artificialmente una onda que tarda 3 segundos en llegar de un extremo al otro de la piscina.

Se observa que la distancia más corta entre dos puntos que se encuentran en oposición de fase para la onda generada es de 75 cm y que en el instante inicial y en el origen de la perturbación la velocidad de oscilación es negativa e igual a 2 m/s y la elongación igualmente negativa de valor 25 cm.

a.- Hallar la fase inicial, la amplitud de la onda y escribir la función de onda.

b.- Hallar la longitud de onda, la velocidad de propagación, la frecuencia angular, la frecuencia en Hz, el periodo.

IR A LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO FÍSICA 2º BACHILLERATO: CAMPO ELECTROSTÁTICO, MAGNÉTICO, ÓPTICA, ONDAS, CUÁNTICA, RELATIVIDAD

ASPECTOS FORMALES PARA DOCENTES, ALCUALIZADOS A LA LOMLOE:

SE PRETENDE CON ESTA DINÁMICA EL DESARROLLO DE LAS COMPETENCIAS: