NÚMEROS COMPLEJOS ARITMÉTICA ÁLGEBRA

NÚMEROS COMPLEJOS. ARITMÉTICA Y ÁLGEBRA PARA BACHILLERATO:NÚMEROS COMPLEJOS ARITMÉTICA ÁLGEBRA

Este contenido supone una profundización / aplicación /consolidación de los RADICALES (por la propia definición de unidad imaginaria), del mismo modo que complementa el ÁLGEBRA en lo que respecta a la resolución de ecuaciones y sistemas de ecuaciones, a través de los ejercicios propuestos.

ASPECTOS FORMALES PARA DOCENTES, AL FINAL DEL ARTÍCULO

ESTE MATERIAL TIENE RELACIÓN CON ASPECTOS DEL PERFIL DE SALIDA DEL ALUMNADO DE LOS INSTITUTOS DIOCESANOS DE CANARIAS

Todo el mundo sabe que:

NÚMEROS COMPLEJOS BACHILLERATO

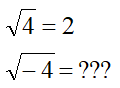
La raíz cuadrada de 4 es 2, porque 22=4

Sin embargo, no tenemos ningún número que elevado al cuadrado nos resulte -4. ¿Cómo resuelven esto los matemáticos?

INTRODUCCIÓN A LOS NÚMEROS COMPLEJOS: https://youtu.be/0JMbIlyylOA

EJERCICIO M1BE2059:

Hallar m y n para que se cumpla la siguiente igualdad:

 (n + 5i) + (2 + mi) = 7 – 2i

IR AL VÍDEO  CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/zkOjMe8SSHY

EJERCICIO M1BE2056:

Determina x para que el producto de números complejos:

z = (2 – 5i) · (3 + xi)  sea,

a.- Un número real.

b.- Un número imaginario.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/CxFLRi8ePm4

EJERCICIO M1BE2308:

Calcular los parámetros m y n para que el producto de los números complejos 3-mi y 4+ni dé como resultado 13-4i.

IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE NÚMEROS COMPLEJOS

EJERCICIO M1BE2058:

Sea z1 = m+i , sea z2 = 1+i, dos números complejos.

Hallar m para que el complejo z = z1/z2 sea igual a 2-i.

IR AL VÍDEO CON LA SOLUCIÓN DEL EJERCICIO: https://youtu.be/KGMzGBohzvs

EJERCICIO M1BE2307:

Calcular el parámetro k para el que número complejo que se muestra, sea imaginario puro:

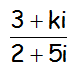
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE NÚMEROS COMPLEJOS

EJERCICIO M1BE2060:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera, expresadas en forma binómica:

 x2 – 2x + 4 = 0

Comprobar con alguna de las soluciones, que realmente lo es.

IR AL VÍDEO QUE SOLUCIONA LA ECUACIÓN: https://youtu.be/TTgx9-6Kzjg

EJERCICIO M1BE2064:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:

 x3 – 6x2 + 21x – 26 = 0

IR AL VÍDEO QUE SOLUCIONA LA ECUACIÓN: https://youtu.be/6C0Fm7LkRZs

EJERCICIO M1BE2065:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:

 x2 + x + 1 = 0

EJERCICIO M1BE2066:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:

 x2 + 4 = 0

EJERCICIO M1BE2083:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:

 x3 + 9x = 0

EJERCICIO M1BE2084:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:

 x2 – 2x + 5 = 0

EJERCICIO M1BE2085:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:

x3 – x2 + 3x + 5 = 0

EJERCICIO M1BE2086:

Halla dos números complejos cuya diferencia es real, su suma tiene como parte real 1 y su producto vale -7+i.

EJERCICIO M1BE2140:

Calcular el parámetro a que hace que el número complejo siguiente sea imaginario puro:

IR AL ARTÍCULO CON LA SOLUCIÓN DEL EJERCICIO: PRUEBA DE ARITMÉTICA Y ÁLGEBRA PARA MATEMÁTICAS 1º BACHILLERATO

EJERCICIO M1BE2342:

Calcular el parámetro k para que el siguiente número complejo sea real:

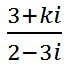
IR A LA RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE NÚMEROS COMPLEJOS

EJERCICIO M1BE2087:

Dados los números complejos 2-mi y 3-ni, hallar los valores que deben tener m y n para que el producto de aquellos sea igual a 8+4i.

EJERCICIO M1BE2088:

Halla dos números complejos cuya diferencia sea imaginaria, su suma tiene como parte imaginaria 5 y su producto vale -5+5i.

EJERCICIO M1BE2089:

Hallar x para que el cociente (x+3i) : (3+2i) se un número imaginario puro.

EJERCICIO M1BE2090:

Calcular a y b de modo que se verifique: (a+bi)2 = 3+4i.

EJERCICIO M1BE2091:

Dados los complejos 2-ai  y  3-bi, hallar a y b para que el producto sea igual a 8+4i

EJERCICIO M1BE2092:

Halla dos números complejos cuya diferencia es real, su suma tiene como parte real 1 y su producto vale -7+i.

EJERCICIO M1BE2093:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:

x3 – 6x2 + 21x – 26 = 0

EJERCICIO M1BE2094:

Resolver la siguiente ecuación, dando todas las soluciones, incluidas las complejas si así fuera el caso, expresadas en forma binómica:

x4 – 3x3 – 2x2 + 10x  = 12

EJERCICIO M1BE2095:

Encontrar el número complejo para el que su cuadrado es igual a 7 + 24 i.

ASPECTOS FORMALES:

CON RESPECTO A LOS SABERES BÁSICOS DE MATEMÁTICAS DE 1º BACHILLERATO PREDOMINANTES EN LA ACTIVIDAD:

CON RESPECTO A LAS COMPETENCIAS ESPECÍFICAS DE MATEMÁTICAS DE 1º DE BACHILLERATO QUE SE CONSIDERAN:

MAT BAC C1 , MAT BAC C2 , MAT BAC C3 , MAT BAC C4 , MAT BAC C5 , MAT BAC C6 , MAT BAC C7 , MAT BAC C8 ,  MAT BAC C9 

CON RESPECTO A LOS CRITERIOS DE EVALUACIÓN DE MATEMÁTICAS I DE 1º DE BACHILLERATO

MATI1BAC1.1 , MATI1BAC1.2 , MATI1BAC2.1 , MATI1BAC2.2 , MATI1BAC3.1 , MATI1BAC4.1 , MATI1BAC5.1 , MATI1BAC5.2 , MATI1BAC6.1 , MATI1BAC6.2 , MATI1BAC7.1 , MATI1BAC7.2 , MATI1BAC8.1 , MATI1BAC8.2 , MATI1BAC9.1 , MATI1BAC9.2 , MATI1BAC9.3 

HIPERVINCULADOS A LOS DESCRIPTORES OPERATIVOS DE LAS COMPETENCIAS CLAVE

CON RESPECTO A LAS COMPETENCIAS CLAVE Y DESCRIPTORES OPERATIVOS ASOCIADOS:

Post Views: 1.664
On:

Comments are closed, but trackbacks and pingbacks are open.