ANÁLISIS FUNCIONES CONTEXTUALIZADO PAU
EJERCICIO M2BE3227 DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADO, PARA MATEMÁTICAS DE BACHILLERATO. PAU CANARIAS JULIO 2025:
PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:
- TABLA DE DERIVADAS
- TASA DE VARIACIÓN MEDIA, INSTANTÁNEA, DERIVADA: DEFINICIÓN. EJERCICIOS RESUELTOS
- INTERPRETACIÓN GEOMÉTRICA DE LA DERIVADA DE UNA FUNCIÓN EN UN PUNTO
- EJERCICIOS DE ANÁLISIS DE FUNCIONES CONTEXTUALIZADOS PARA MATEMÁTICAS DE BACHILLERATO
- ANÁLISIS DE FUNCIONES PARA BACHILLERATO
- INTEGRALES Y DERIVADAS. PROBLEMAS CONTEXTUALIZADOS
- ANÁLISIS EN PROFUNDIDAD DE UN MOVIMIENTO VARIADO COMO APLICACIÓN DE LAS DERIVADAS E INTEGRALES EN FÍSICA. PROBLEMAS CONTEXTUALIZADOS.
FORMA PARTE DEL PROCESO DETERMINADO POR LA PROPUESTA DE PROGRAMACIÓN DIDÁCTICA:
EJERCICIO M2BE3227: PAU CANARIAS JULIO 2025
El modelo logístico es un modelo matemático utilizado para describir la evolución de una población a lo largo del tiempo, cuando los recursos son limitados. Es uno de los modelos matemáticos más comunes en biología y describe cómo la población se estabiliza cuando alcanza la capacidad de carga del entorno, esto es, el tamaño máximo que puede alcanzar una población antes de que los recursos se vuelvan insuficientes, lo que genera competencia y, en muchos casos, una desaceleración de la tasa de crecimiento o una crisis en la población.
Un ejemplo de modelo logístico lo encontramos en las colonias de hormigas, que están compuestas por una red de túneles, entradas, cámaras de cría y áreas de almacenamiento, donde las hormigas establecen su hábitat.
Un grupo de investigadores ha estudiado el momento en el que unas hormigas forman una nueva colonia y ha modelizado el número de hormigas (H(t)) después de t meses con la función:
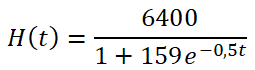
a) ¿Cuántas hormigas formaron la nueva colonia inicialmente?
b) ¿Cuál es la tasa media de crecimiento el primer año? ¿Y el segundo año? Interpretar el resultado.
PARA ESTE APARTADO PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE ARTÍCULO: TASA DE VARIACIÓN MEDIA, INSTANTÁNEA, DERIVADA: DEFINICIÓN. EJERCICIOS RESUELTOS
c) Un observador afirma que el modelo siempre es creciente y entiende que la población de hormigas crece sin control. Justificar matemáticamente si esta afirmación es o no correcta.
d) ¿En qué momento la colonia de hormigas alcanzará la mitad de su capacidad de carga?
RESOLUCIÓN PASO A PASO DE ESTE EJERCICIO DE ANÁLISIS DE FUNCIONES:


