POSICIONES RELATIVAS RECTAS PLANO GEOMETRÍA
MATEMÁTICAS I 1º BACHILLERATO CIENCIAS
POSICIONES RELATIVAS DE DOS RECTAS EN EL PLANO PARA MATEMÁTICAS DE SECUNDARIA Y BACHILLERATO. GEOMETRÍA ANALÍTICA:

PUEDE INTERESAR LA CONSULTA DEL SIGUIENTE MATERIAL RELACIONADO:
SIGUE EL PROCESO DETERMINADO SEGÚN:
POSICIONES RELATIVAS DE DOS RECTAS EN EL PLANO, GEOMETRÍA EN DOS DIMENSIONES (M3P44-45):
Dos rectas en el plano pueden ser:
- SECANTES, si se cortan en un punto.
- PARALELAS, en cuyo caso no se cortan.
- COINCIDENTES, si son la misma recta. Se puede considerar un caso particular de rectas paralelas.
Como siempre que queremos saber, si dos elementos tienen algún punto en común, puntos de cortes, se resuelve el sistema formado por las ecuaciones de los respectivos elementos.
Cuando resolvemos el sistema formado por las dos rectas:
- Si el sistema tiene una solución, nos indica que se cortan en un punto, el de la solución.
- Si el sistema no tiene solución, las rectas son paralelas.
- Si el sistema tiene infinitas soluciones, las rectas son coincidentes, son la misma recta.
La forma más usual es la de trabajar con el SISTEMA DE ECUACIONES EN FORMA GENERAL (IMPLICITA):
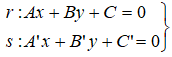
Antes de empezar a trabajar con el sistema se pueden sacar conclusiones con el análisis de los coeficientes de cada una de las ecuaciones:
Sabemos que la A y la B de la ecuación en forma implícita corresponden a las componentes del director de la recta (a,b), del siguiente modo: A = b ; B = – a .
Con esto podemos sacar las componentes de los directores de las dos rectas. Si los directores son proporcionales esto es, por ejemplo: d=(1,3); d’=(-2,-6), estaríamos en el caso general de rectas paralelas, que podrían ser coincidentes. En caso contrario, las rectas se cortarían en un punto (secantes) y al resolver el sistema por cualquiera de los métodos tradicionales nos daría el punto de corte.
Cuando dos rectas son coincidentes, es que son la misma recta, lo único que ocurre es que una de ellas es la otra multiplicada por un número. En este caso son proporcionales todos los coeficientes A,B y C.
La forma matemática de identificar si las componentes de los directores (o los coeficientes de la ecuación en forma general) son proporcionales es realizar el cociente de los coeficientes:
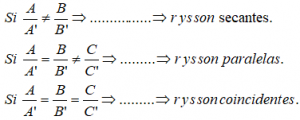
En el caso en que sean secantes es imprescindible buscar el punto de corte, en los otros casos una vez identificada la situación no hay que realizar más cálculos.
También se pueden expresar las ecuaciones de las rectas que intervienen en el SISTEMA DE ECUACIONES EN FORMA EXPLÍCITA:
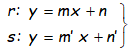
En este caso es más inmediato la identificación de la situación, ya que si las pendientes son iguales (m de cada ecuación), las rectas son paralelas en sentido amplio (pueden ser además coincidentes). Si las pendientes son distintas, se cortan y lo único que resta es calcular el punto de corte resolviendo el sistema por cualquiera de los métodos tradicionales.
Cuando las pendientes son iguales, para distinguir el caso de coincidentes y paralelas sólo hay que ver el resto de la ecuación, la n (ordenada en el origen), y si coinciden además de coincidir las m, son coincidentes (la misma ecuación, la misma recta), en caso contrario paralelas.
El esquema de lo que acabamos de decir:
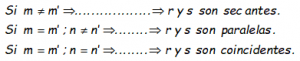
Si en nuestro ejercicio las ecuaciones no están en las formas anteriores, bastará con pasarlas a cualquiera de ellas y seguir el proceso marcado.
EJERCICIO M1BE3461-6:
Determina la posición relativa de los siguientes pares de rectas. En caso de que sean secantes, determina el punto de intersección:
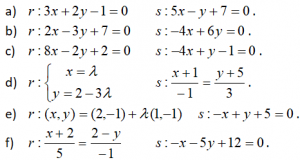
EJERCICIO M1BE3461-7:
Dadas las rectas r y s, determinar k para que sean perpendiculares:
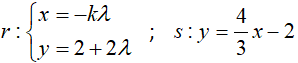
EJERCICIO M1BE3461-10:
Dadas las rectas r y s siguientes:
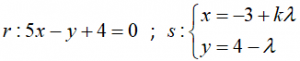
determinar el valor de k para que las rectas r y s sean:
a.- Paralelas.
b.- Perpendiculares.
EJERCICIO M1BE3462-3:
Determina la posición relativa de estas rectas. Si se cortan, di en qué punto:
![]()
EJERCICIO M1BE3462-4:
Determina el ángulo que forman las rectas:

EJERCICIO M1BE3463-1:
Determinar el valor de a para que las rectas: ax + (a-1) y – 2(a+2) = 0 y 3ax – (3a+1)y – (5a+4) = 0 sean:
- paralelas
- perpendiculares
EJERCICIO M1BE3463-2:
Determinar el valor de m para que las rectas: mx +y = 12 y 4x – 3y = m+1 sean paralelas.
