APLICACIONES DERIVADA MONOTONÍA CURVATURA

APLICACIONES DE LA DERIVADA: MONOTONÍA Y CURVATURA PARA MATEMÁTICAS DE BACHILLERATO:

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

EJERCICIO M1BE3127:

Calcular de la siguiente función polinómica: f(x) = x³– 3x² + 4

a) Cortes con los ejes.

b) La monotonía y los extremos relativos.

c) La curvatura y los puntos de inflexión.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO CIENCIAS Y TECNOLOGÍA. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 2024-25

EJERCICIO M1BE2405:

Representar la función:

f(x) = x³ – x² – x + 1

Obteniendo el dominio, puntos de corte con los ejes, extremos y monotonía. puntos de inflexión y curvatura, simetrías.

IR AL ARTÍCULO CON LA CLASE ON LINE Y VÍDEO QUE RESUELVE ESTE EJERCICIO Y OTROS DE ANÁLISIS DE FUNCIONES: CLASE ONLINE DE ANÁLISIS DE FUNCIONES. PROGRAMA DE REFUERZO DE MATEMÁTICAS DE BACHILLERATO

EJERCICIO M1BE2218:

Siendo f(x) = 2x³– 5x²– 4x , realizar los siguientes apartados:

a.- Monotonía y máximos y mínimos.

b.- Curvatura y puntos de inflexión.

IR AL ARTÍCULO CON LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO

EJERCICIO M1BE2420:

Representar la siguiente función polinómica, f(x) = x³+ 2x²– x – 1, obteniendo previamente todo lo que resulte significativo. Realizar posteriormente el contraste con geogebra.

IR A LA RESOLUCIÓN PASO A PASO DEL EJERCICIO: TRABAJO TRIMESTRAL DE REPRESENTACIÓN DE FUNCIONES PARA MATEMÁTICAS I DE 1º BACHILLERATO

EJERCICIO M1BE2474:

Para la siguiente función polinómica, f(x) = x³ + 3x² – 4x , calcular:

a.- La monotonía y los extremos relativos.

b.- La curvatura y los puntos de inflexión.

IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: EXAMEN RESUELTO DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS I DE 1º DE BACHILLERATO. PRUEBA 1 DEL TERCER TRIMESTRE DEL CURSO 23-24.

EJERCICIO M2BE2227: (MONOTONÍA Y EXTREMOS)

Calcula los intervalos de crecimiento-decrecimiento y los máximos-mínimos de la función,

f(x) = (x²+3x+1) · e^-x

IR A LA RESOLUCIÓN DEL EJERCICIO: EJERCICIO RESUELTO M2BE2227 DE APLICACIONES DE LA DERIVADA: MONOTONÍA (INTERVALOS DE CRECIMIENTO Y DECRECIMIENTO), EXTREMOS Y CURVATURA.

EJERCICIO M1BE2004:

Considera la función:

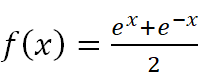
a) Estudia y determina los intervalos de crecimiento y los intervalos de decrecimiento de f. Calcula los extremos relativos de f (abscisas donde se obtienen y valores que se alcanzan).

b) Halla la ecuación de la recta normal a la gráfica de f en el punto de abscisa x = 0.

EJERCICIO M2BE2277:

Dada la siguiente función f(x):

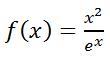
a.- Determinar los intervalos de crecimiento y los de decrecimiento.

b.- Calcular los máximos y mínimos relativos.

IR A LA SOLUCIÓN PASO A PASO DE ESTE EJERCICIO: EXAMEN DE ANÁLISIS DE FUNCIONES PARA MATEMÁTICAS II DE 2º DE BACHILLERATO. CURSO 2023-24

EJERCICIO M1BE2305:

Para la función f(x) que se añade, realizar los siguientes apartados:

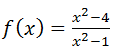
a) Dominio.

b) Asíntotas.

c) Cortes con los ejes.

d) Monotonía y extremos relativos.

e) Representar la función.

IR AL ARTÍCULO CON LA RESOLUCIÓN DEL EJERCICIO: PROPUESTA DE EVALUACIÓN FUNCIONES 1º BACHILLERATO

EJERCICIO M2BE309:

El dueño de un manantial de agua mineral llega a la siguiente conclusión: si el precio a que vende la botella es x euros, sus beneficios serán de –x²+10x-21 miles de euros al mes. Hallar:

a) ¿Qué precio debe poner para obtener un beneficio máximo?

b) ¿Cuál será ese beneficio?

c) ¿Entre que precios obtiene beneficios el agricultor?

d) Representar la función.

IR A LA RESOLUCIÓN DE ESTE EJERCICIO

EJERCICIO M2BE3386:

Para la siguiente función f(x):