ÁREAS LIMITADAS FUNCIÓN OX

ÁREAS LIMITADAS POR UNA FUNCIÓN Y EL EJE OX. APLICACIONES DE LA INTEGRAL DEFINIDA:

ÁREAS LIMITADAS FUNCIÓN OX

PUEDE INTERESAR LA CONSULTA DE LOS SIGUIENTES ARTÍCULOS RELACIONADOS:

SIGUE EL PROCESO DETERMINADO POR:

CÁLCULO DE ÁREAS LIMITADAS POR UNA FUNCIÓN Y EL EJE OX, UTILIZANDO LA INTEGRAL DEFINIDA:

El cálculo de áreas limitadas por la función y el eje de abscisas presenta un problema a nivel práctico y es que si la función es negativa, se encuentra por debajo del eje de las x, la integral también lo es. Por ello, desde el punto de vista práctico lo que se hace es lo siguiente, según estos tres casos:.

A) SI LA FUNCIÓN ES TODA POSITIVA, DESDE a HASTA b:

(Se encuentra por encima del eje OX), el resultado de la integral definida es igualmente positivo y coincide con el área del recinto determinado por la función, el eje X y las rectas x=a y x=b.

B) SI LA FUNCIÓN ES TODA NEGATIVA, DESDE a HASTA b:

(Se encuentra por debajo del eje OX), el resultado de la integral definida es negativo, pero en valor absoluto coincide con el área del recinto, por lo que:

C) Si la función desde a hasta b, toma valores POSITIVOS Y NEGATIVOS:

Generando recintos de áreas por encima y debajo del eje OX, en subintervalos (corta al eje de las x en uno o varios puntos), el resultado de la integral definida de a hasta b, compensa las áreas positivas con las negativas, dando un resultado que no es el que se nos pide. Lo que se hace en estos casos es localizar los puntos de corte de la función con el eje X que se encuentran entre a y b, y ordenarlos de mayor a menor empezando en a y terminando en b, entonces, el área:

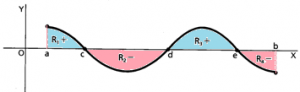
Se subdivide en integralitas más pequeñas, utilizando los valores absolutos para que las áreas positivas no compensen las negativas y el resultado realmente coincida con el área

 

CONTINUAR CON:

Visualizaciones: 5
On: